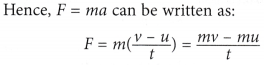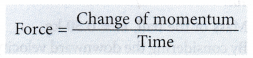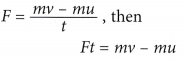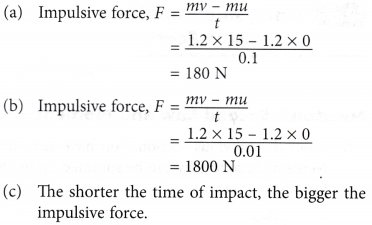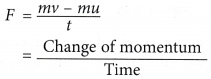momentum Archives

How Do You Solve For Momentum

December 18, 2020December 18, 2020 by Veerendra

What Is Momentum

momentum

Every moving object has momentum. However, the momentum of a timber lorry is very much bigger than that of a cyclist, despite them moving at the same speed.
The product of mass and velocity is called ‘momentum‘.
\(\text{i}\text{.e}\text{. }p=m\overset{\to }{\mathop{v}}\)
Unit: SI unit of momentum is kg-m/s.
It is a vector quantity.

Also Read About: Principle of Conservation of Momentum

Activity 1

Aim: To study the effect of stopping two objects
A. of the same mass moving at different speeds
B. of different masses moving at the same speed
Materials: Two identical glass marbles, soft plasticine, a steel marble of the same size as the glass marbles but with a bigger mass
Apparatus: Meter ruler, vernier callipers
Method:
A. Same Mass Moving at Different Speeds
momentum 1

Two identical pieces of soft plasticine are placed on a table.
A glass marble is dropped on the plasticine from a height of 20 cm. Another identical glass marble is dropped on the other piece of plasticine from a height of 60 cm as shown in Figure (a).
The diameter of the cavity on the surface of each plasticine caused by the falling marbles is measured using a pair of vernier callipers and compared.

B. Different Masses Moving at the Same Speed
momentum 2

The method in section A is repeated by releasing a glass marble and a steel marble of the same size, both from a height of 60 cm.

Results:
A. Same Mass Moving at Different Speeds
The diameter of the cavity on the surface of the plasticine caused by the glass marble that is dropped from a height of 60 cm is larger than that caused by the glass marble that is dropped from a height of 20 cm.
B. Different Masses Moving at the Same Speed
The diameter of the cavity on the surface of the plasticine caused by the steel marble is larger than that caused by the glass marble.
Discussion:
A larger cavity on the surface of the plasticine caused by a falling marble means a bigger effect on the plasticine in stopping the marble. The size of the cavity is a measure of the magnitude of the momentum of the moving object.
A. Same Mass Moving at Different Speeds

The glass marble that is dropped from a higher height will reach the surface of the plasticine with a higher speed.
Both marbles are identical and hence, they have the same mass. Therefore, for two objects of equal mass, stopping the one with a higher speed requires greater effort than the one with a lower speed.

B. Different Masses Moving at the Same Speed

Both the glass marble and the steel marble are dropped from the same height. Therefore, both of them will reach the surface of the plasticine with the same velocity.
The steel marble has a greater mass than the glass marble. Therefore, for two objects of different masses but moving at the same speed, the effect of stopping the one with a bigger mass is greater than the one with a smaller mass.

Conclusion:
The linear momentum of an object depends on its mass and speed. For an object with constant mass, the higher its speed, the higher is its momentum. For an object with constant speed, the larger its mass, the higher is its momentum.

Momentum Example Problems With Solutions

Example 1. Calculate the force required to produce an acceleration of 5 m/s² in a body of mass 2.4 kg.
Solution: We know that force = mass × acceleration
= 2.4 kg × 5 m/s²
= 12.0N

Example 2. A body of mass 2.5 kg is moving with a velocity of 20 m/s. Calculate its momentum.
Solution: Momentum, p = mass × velocity
Here, mass m = 2.5 kg
Velocity, v = 20 m/s
∴ Momentum, p = mv = 2.5 × 20 kg-m/s
= 50 kg-m/s

Example 3. The total mass of a lorry is 20000 kg and the total mass of a car is 2000 kg.
If both the lorry and the car are travelling at a velocity of 25 m s^-1, calculate the momentum of the lorry and the car respectively.
Solution:
Momentum of the lorry = 20000 × 25
= 5 × 10⁵ kg m s^-1
Momentum of the car = 2000 × 25
= 5 × 10 kg m s^-1

What is Law of Conservation of Momentum

December 18, 2020December 18, 2020 by Veerendra

Law of Conservation of Momentum

According to law of conservation of momentum “if there is no force acting on a system, the momentum of the system remains unchanged.”
Generalizing the situation ” if a group of bodies are exerting force on each other, their total momentum remains conserved before and after the interaction provided there is no external force acting on them.”
i.e. m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

Definition of Principle of Conservation of Momentum
The principle of conservation of momentum can also be defined as follows:

The total momentum in a closed system is constant.
A system consists of several objects acting on each other.
A closed system is a system where the sum of its external forces (also known as resultant force) is zero.
When the momentum is constant, we say the momentum is conserved.

Figure shows two billiard balls, A and B. When ball A collides with ball B, ball A loses momentum and ball B gains the amount of momentum lost by ball A.
Figure (a) shows a boy standing on a skating board with a bowling ball in his hands.
When he throws the ball forward, he moves backward. Initially, the respective momentums of both the boy and the ball is zero because both are at rest.
When the ball is thrown, the ball gains momentum. The boy gains an equal amount of momentum but in the opposite direction.
The above observations can be explained using the principle of conservation of momentum.
According to the principle of conservation of momentum, when two or more bodies act on each other, their total momentum remains constant, provided that there is no external force acting on them.

Experiment 1

Aim: To show that the total momentum of a closed system is conserved.
Problem: Is the total momentum in a closed system constant?
Hypothesis: The total momentum of a system after a collision/explosion is the same as the total momentum before the collision/explosion.
A. Collision
Materials: Cellophane tape, ticker tape, plasticine, two pins, two pieces of cork
Apparatus: Trolleys, plane, retort stands with clamps, power supply
Variables:
(a) Manipulated variable: Mass of trolley
(b) Responding variable: Velocity of trolley
Method:
Law of conservation momentum 1

The apparatus is set up by attaching two pins in front of trolley P and two pieces of cork at the end of trolley Q as shown in Figure.
Trolley P is placed at the higher end of the plane and trolley Q is placed halfway down the plane and is at rest. A ticker tape is passed through the ticker timer and is attached to trolley P.
After the ticker timer is switched on, trolley P is given a push towards trolley Q. Both trolleys will stick together and move down the plane after the collision.
The tapes are analysed to determine the following:
(a) velocity of trolley P before the collision, u_p.
(b) velocity of trolley P and trolley Q after the collision, v.
Using identical trolleys, the mass of each trolley can be taken as 1 unit of mass. The experiment is repeated as follows:
(a) two stacked trolleys collide with one trolley at rest,
(b) three stacked trolleys collide with one trolley at rest.

Results:
Law of conservation momentum 2
Discussion:
Before collision, velocity of trolley Q, u_Q = 0 because it is at rest.
Conclusion:
It is found that the total momentum after the collision is the same as that before the collision. The hypothesis is accepted.

B. Explosion
Materials: Cellophane tape, ticker tape, mallet
Apparatus: Trolleys, power supply
Variables:
(a) Manipulated variable: Mass of trolley
(b) Responding variable: Velocity of trolley
Method:
Law of conservation momentum 3

Trolley P and trolley Q are set up facing each other on a smooth table as shown in Figure (a). The spring-loaded plunger of trolley P is compressed.
Two ticker tapes are passed through the ticker timer, one attached to trolley P and another to trolley Q.
After the ticker timer is switched on, the plunger of trolley P is released by tapping the release dowel rod with a mallet. The trolleys will ‘explode’ and move apart in opposite directions as shown in Figure (b).
From the tapes obtained, the velocities of trolley P, vp and trolley Q, v_Q are determined.
The experiment is repeated by using two and then three stacked trolleys placed facing trolley Q.

Results:
Law of conservation momentum 4
Discussion:

In the case of an explosion system, the total momentum before the explosion is always zero because all the bodies in the system are at rest initially.
Since trolley P and trolley Q move in opposite directions, if we assign v_P to be positive, then v_Q will be negative.

Conclusion:
It is found that the total momentum before and after the explosion are the same and both are equal to zero. The hypothesis is accepted.

Applications of Conservation of Momentum

(a) Figure shows the launching of a rocket. A rocket carries liquid hydrogen fuel and liquid oxygen. When a mixture of hydrogen and oxygen burns in the combustion chamber during launching, jets of hot gas are expelled at very high speed through the exhausts. This produces a very large momentum.
Fig. A rocket

(b) According to the principle of conservation of momentum, an equal and opposite momentum is produced causing the rocket to propel upwards.
(a) Figure shows a jet engine. Air in front of the engine is sucked into the combustion chamber by the rotating compressor blades. In the combustion chamber, fuel is injected and burnt with the compressed air.
Fig. A jet engine

(b) The exploding hot jet of gases is expelled from the combustion chamber. This produces a very large momentum.
(c) According to the principle of conservation of momentum, the expulsion of the hot gases produces an equal and opposite momentum, causing the jet plane to move forward.
(a) When a bullet is fired from a submachine gun, the exploding gases from the bullet cause it to be shot out at a very high speed, producing a very big momentum.
Fig. A rifle

(b) An equal and opposite momentum is produced and this causes the submachine gun to recoil.

Law of Conservation of Momentum Example Problems with Solutions

Example 1. A rifle of mass 5 kg fires a bullet of mass 40 gm. The bullet leaves the barrel of the rifle with a velocity 200 m/s. If the bullet takes 0.004 s to move through the barrel, calculate the following:
(i) recoil velocity of the rifle and
(ii) the force experienced by the rifle due to its recoil.
Solution: (i) Given mass of the rifle, m₁ = 5 kg
Mass of the bullet, m₂ = 40 gm = 0.04 kg
Initial velocities, u₁ = 0, u₂ = 0
After firing velocity of the bullet, v₂ = 200 m/s
Velocity of the rifle, v₁ = ?
Applying the law of conservation of momentum, we get
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
0 + 0 = 5 × v₁ + 0.04 × 200
\({{v}_{1~}}=\frac{0.04\times 200}{5}=-1.6\text{ m/s}\)
(ii) Initial momentum of the rifle = 0
Final momentum of the rifle = 5 kg ×(–1.6)
= – 8 kg-m/s
Time interval = 0.004 s
\( \therefore \text{Force}=\frac{\text{Change}\,\text{in}\,\text{momentum}}{\text{Time}\,\text{interval}} \)
\( =\frac{-8kg-m{{s}^{-1}}}{0.004}=-2000\text{ N} \)

Example 2. A bullet of mass 20 gm moving with a velocity 200 m/s gets embedded into a wooden block of mass 980 gm suspended by a string. Calculate velocity acquired by the combined system.
Solution: Mass of the bullet, m₁ = 20 gm = 0.02 kg
Velocity of the bullet, u₁ = 200 m/s
Momentum of the bullet = m₁u₁
= 0.02 × 200 kg-m/s = 4 kg-m/s
Now, the bullet gets embedded into a wooden block of mass 980 gm. The mass of the block and bullet = 980 + 20
= 1000 gm = 1kg
Let the velocity of the combined system = v
∴ Momentum of the combined system
= 1 × v kg-m/s = v kg-m/s
Now, applying the law of conservation of momentum,
m₁u₁ = (m₁ + m₂)v
or 4 = v
∴ v = 4 m/s = 4 kg m/s

Example 3. A rifle man, who together with his rifle has a mass of 100 kg, stands on a smooth surface fires 10 shots horizontally. Each bullet has a mass 10 gm a muzzle velocity of 800 m/s. What velocity does rifle man acquire at the end of 10 shots?
Solution: Let m₁ and m₂ be the masses of bullet and the rifleman and v₁ and v₂ their respective velocities after the first shot. Initially the rifleman and bullet are at rest, therefore initial momentum of system = 0.
As external force is zero, momentum of system is constant
i.e. initial momentum = final momentum
= m₁v₁ + m₂v₂
\(\Rightarrow {{v}_{2}}=\frac{{{m}_{1}}{{v}_{1}}}{{{m}_{2}}}=-\frac{(10\,\times \,{{10}^{-3}}kg)(800\,m/s)}{100kg}\)
= – 0.08 m/s
Velocity acquired after 10 shots
= 10 v₂ = 10 x (–0.08)
= – 0.8 m/s.
i.e, the velocity of rifle man is 0.8 m/s in a direction opposite to that of bullet.

Example 4. A body of mass 1 kg strikes elastically with another body at rest and continues to move in the same direction with one fourth of the initial velocity. What will be the mass of the other body ?
Solution: Given that,
Initial velocity = u
Final velocity = \(\frac { u }{ 4 }\)
So by conservation of momentum, we have
1 × u + 0 = 1 × \(\frac { u }{ 4 }\) + m × v₂
⇒ mv₂ = \(\frac { 3u }{ 4 }\) …(1)
and by conservation of energy, we have
\( \Rightarrow \frac{1}{2}\times 1\times {{u}^{2}}+0=~~\frac{1}{2}\times 1~{{\left( \frac{u}{4} \right)}^{2}}+~m{{v}_{2}}^{2}\)
\(\Rightarrow \text{m}{{\text{v}}_{\text{2}}}^{\text{2}}=\frac{15}{16}{{u}^{2}}\text{ }……\text{ (2)}\)
from equation (1) and (2),
\(=\frac{{{(m{{v}_{2}})}^{2}}}{mv_{2}^{2}}=\frac{(9/16){{u}^{2}}}{(15/16){{u}^{2}}}\)
or m = 0.6 kg

Example 5. Figure shows two rocks moving towards each other along a straight line. After colliding with each other, the two rocks lump together.
Calculate the speed of the rocks after the collision.
Law of conservation momentum 8
Solution:
Law of conservation momentum 9

Example 6. An astronaut with mass of 80 kg throws a 40 kg tool box in order to be able to get back to the space capsule.
If the box is thrown at a velocity of 6 m s^-1, what is the velocity of the astronaut after throwing the tool box?
Law of conservation momentum 10
Solution:

Example 7. Figure shows two identical boxcars of a train being coupled at a railway station. Each boxcar has a mass of 2.5 × 10⁴ kg. The velocities of boxcar 1 and boxcar 2 before the coupling are 1.0 m s^-1 and 0.8 m s^-1 respectively.
Find the velocity, v, of the boxcars after they are coupled. State one assumption in your calculation.
Law of conservation momentum 12
Solution:

How Impulse is Related to The Change in Momentum

December 18, 2020December 18, 2020 by Veerendra

Impulse of Force

From the previous section, you have seen that Newtons Second Law can be summed up by the formula F = ma. How Impulse is Related to The Change in Momentum When a net force acts on a body, it accelerates in the direction of the force. By definition, acceleration, a is the rate of change in velocity and is given by the formula:

How Impulse is Related to The Change in Momentum 1

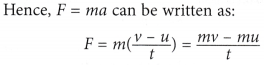
Since (mv – mu) is the change of momentum, therefore,

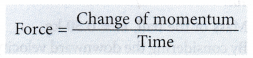
or force is equal to the rate of change of momentum.

Impulse and Impulsive Force

If a force F is applied on a body of mass m for a time interval Δt and if the change in velocity is Δv then
∴ Impulse = F dt = m Δ v
Impulse = change in momentum

Since
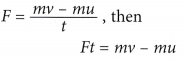
The quantity (Force x Time) is called the impulse of a force.
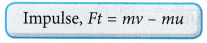
The SI unit for impulse is newton seconds (N s).
Impulse is a vector quantity and has the same direction as the applied force.
From the equation,

the force is known as the impulsive force.
Hence, impulsive force is defined as the rate of change of momentum.

Example: While catching a cricket ball a player moves his hands backwards. Cricket ball coming towards fielder has a large momentum. By doing so he increases the time interval to reduce the momentum of the ball. Rate of change of momentum becomes slow.

Impulse of Force Example Problems with Solutions

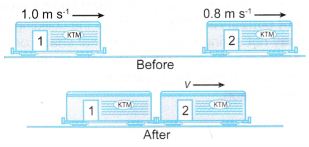
Example 1. A boy hits a 0.50 kg ball and sends it moving in the opposite direction. Figure shows the magnitudes of its velocity before and after being hit respectively. The time of contact between the hand and the ball is 0.05 s.
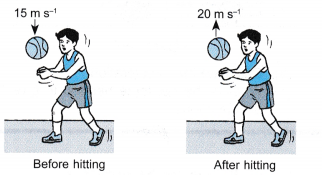
How Impulse is Related to The Change in Momentum 7
Calculate
(a) the impulse applied to the ball,
(b) the impulsive force exerted on the ball by the hands.
Solution:

(The negative sign shows that the force is acting against the initial direction of motion of the ball)

Example 2. Figure shows a boy kicking a football and a rock.
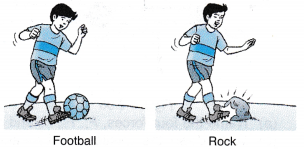
How Impulse is Related to The Change in Momentum 9
(a) From Figure, when the boy kicks the 1.2 kg football, it moves from rest to 15 m s^-1 in 0.1 s. Calculate the impulsive force exerted on the ball.
(b) The boy then kicks a rock of the same mass and it moves from rest to 15 m s^-1. However, due to the rigidity of the rock, the time which the foot acts on the rock is only 0.01 s. What is the impulsive force exerted on the rock?
(c) From the answers in (a) and (b), what is the relationship between the time of impact and the impulsive force?
Solution:
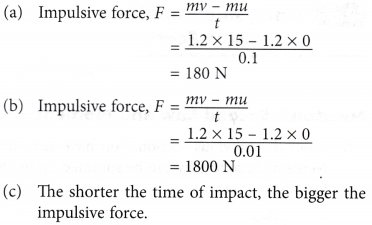
How Impulse is Related to The Change in Momentum 10

Example 3. A force acts for 0.2 s on a body of mass 2.5 kg initially at rest. The force then ceases to act and the body moves through 4m in the next one second. Calculate the magnitude of force.
Solution: When the force ceases to act, the body will move with a constant velocity. Since it moves a distance of 4 m in 1 s, therefore, its uniform velocity = 4m/s.
Now, initial velocity, u = 0
Final velocity, v = 4 m/s
Time interval Δt = 0.2 s
∴ Acceleration,
\(a=\frac{v-u}{\Delta t}=\frac{4-0}{0.2}=\text{20 m/}{{\text{s}}^{\text{2}}}\)
Force, F = 2.5 × 20 = 50 N

Example 4. A ball of mass 20 gm is initially moving with a velocity of 100 m/s. On applying a constant force on the ball for 0.5s, it acquires a velocity of 150 m/s. Calculate the following
(i) Initial momentum of the ball
(ii) Final momentum of the ball
(iii) Rate of change of momentum
(iv) Acceleration of the ball
(v) Magnitude of the force applied
Solution: Given, m = 20 gm = \(\frac { 20 }{ 1000 }\) kg = 0.02 kg
Initial velocity, u = 100 m/s
Time interval, t = 0.5 s
Final velocity, v = 150 m/s
(i) Initial momentum of the ball = mass × initial velocity
P₁ = mu = 0.02 kg × 100 m/s
= 2 kg-ms^-1
(ii) Final momentum of the ball = mass × final velocity
P₂ = mv = 0.02 kg × 150 m/s
= 3 kg-ms–1
(iii) Rate of change of momentum
\(=\frac{\text{Final}\,\text{momentum}\,\text{-}\,\text{Initial}\,\text{momentum}}{\text{Time}}\)
\( \Rightarrow \frac{\Delta P}{\Delta t}=\frac{3-2}{0.5}=\frac{1}{0.5} \)
⇒ 2.0 kg-ms^-1 = 2.0N
(iv) Acceleration,
\( a=\frac{v-u}{t}=\frac{150-100}{0.5} \)
= 100 ms^-2
(v) Force, F = mass × acceleration
= 0.02 × 100 = 2.0 N

Example 5. A cricket ball of mass 200 gm moving with a speed of 40 m/s is brought to rest by a player in 0.04s. Calculate the following :
(i) change in momentum of the ball,
(ii) average force applied by the player.
Solution: Mass, m = 200 gm = 0.2 kg
Initial velocity, u = 40 m/s
Final velocity, v = 0
Time, t = 0.04 s
(i) Initial momentum, P₁ = mu = 0.2 kg × 40 m/s
= 8.0 kg-ms^-1
Final momentum, p₂ = m × v = 0.2 × 0
= 0 kg-ms^-1
Change in momentum, Δp = P₁ – P₂
= 0 – 8.0 kg ms^-1= – 8.0 kg-ms^-1
\( \left( \text{ii} \right)\text{ Average force }=\frac{\text{Change}\,\text{in}\,\text{momentum}}{\text{Time}}\text{ } \)
\( \text{=}\frac{-8.0-0}{0.04}=-200\text{ N} \)
(The negative sign shows that the force is applied in a direction opposite to the direction of motion of the ball).

Example 6. A motorcycle is moving with a velocity of 108 km/hr and it takes 5 s to stop it after the brakes are applied. Calculate the force exerted by the brakes on the motorcycle if its mass along with the rider is 250 kg.
Solution: Given that initial velocity of the motorcycle
= 108 km/hr = 30 m/s
Final velocity = 0 m/s
Time taken to stop = 5s, the mass of the motorcycle with rider = 250 kg.
The change in the velocity of the motorcycle in 5s = 0 – 30 = –30 m/s
Therefore, the acceleration of the motorcycle,
a = \(\frac { -30 }{ 5 }\) = –6 m/s²
The magnitude of the force applied by the brakes is given by the equation,
F = mass × acceleration
= 250 kg × (6) m/s² = 1500 N

The Effect of Time on the Magnitude of the Impulsive Force

Consider the formula for impulsive force:
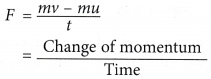
How Impulse is Related to The Change in Momentum 11
If the change of momentum is constant, the magnitude of the impulsive force is inversely proportional to the time of impact.
That is, F ∝ 1/t
Since F ∝ 1/t, the shorter the time of impact, the bigger the impulsive force. The longer the time of impact, the smaller the impulsive force. Hence, by controlling the value of f, we can control the value of the impulsive force, F.

Increasing the time of impact, t to reduce the impulsive force, F

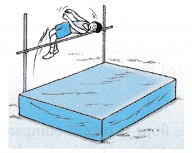
When a high jumper falls on a mattress, the thick and soft mattress lengthens the time of impact. The impulsive force acting on the high jumper is reduced and he is less likely to suffer any injury.
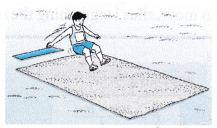
A long jumper lands on a pit filled with loose sand. The loose sand lengthens the time of impact and reduces the impulsive force acting on him.
Figure shows a baseball player stopping a fast moving ball with his hand.

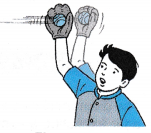
(a) The glove which is made of soft material lengthens the time of impact and reduces
the impulsive force acting on his palm.
(b) When catching the ball, the player moves his hand backward. This action will lengthen the time of impact between the ball and the glove and further reduce the impulsive force acting on his palm.
(c) The combined effect of the glove and the action of the hand prevents injury to the player.

Decreasing the time of impact, t to increase the impulsive force, F

Pestle and mortar are made of stone. The pestle is used to pound spices like chilli, onion and garlic. The impact time between the pestle and the mortar is very short because of their hard and rigid surfaces. The large impulsive force causes the spices to be crushed easily.
A blacksmith uses a heavy hammer and anvil to forge metals. An anvil, which is made of steel, has a very hard surface. When the hammer knocks on a piece of metal placed on the anvil, the short impact time causes a large impulsive force to act on the metal.
A golf club has very hard hitting surfaces to give a big force on the balls. The hard surface gives a short impact time and a large impulsive force.

Example 1. Explain why it is easier to drive a nail into a plank if the plank is placed on a concrete floor compared to a grass covered floor.
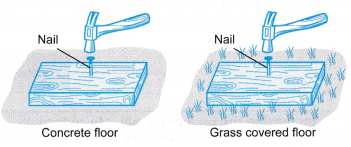
How Impulse is Related to The Change in Momentum 18
Solution:
The concrete floor is harder compared to the grass covered floor. If the plank is placed on the concrete floor, it will not move when the hammer strikes the nail. As a result, the impact time between the hammer and the nail is short and the impulsive force is big.
A soft surface like the grass covered floor will cause the plank to move, thus lengthening the impact time.