Law Of Conservation Of Momentum

Newton’s Laws Of Motion

by

Newton’s Laws Of Motion

(A) Newton’s First Law of Motion

A body can not change its state of motion by itself. If the object is at rest it will remain at rest and if it is in uniform motion, it continues to be in motion unless some external force is applied on it.

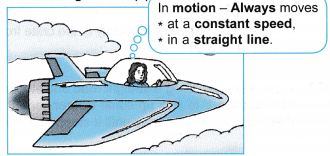
  1. Newton’s First Law of Motion states that if there is no net force acting on a body, its state of motion will be unchanged.
  2. If the body is at rest, it will remain at rest. If the body is moving, it keeps on moving at a constant speed in a straight line.
  3. Newton’s first law is sometimes called the Law of Inertia.
  4. The object is not necessarily at rest. The object may be moving at constant speed in a straight line.
  5. To remember Newton’s First Law of Motion
    When F = 0 (No resultant force)
    Understanding inertia 1
    Understanding inertia 2

Inertia:
There is an inherent property of an object by virtue of which it cannot change its state of motion or rest by itself. This property is called ‘inertia’.
Inertia is of two types– inertia of rest and inertia of motion.

(a) Inertia of rest: If the body is at rest, it will continue to be at rest unless some external force is applied on it. Examples are following.
Examples:
1. When a train at rest starts moving suddenly, a passenger standing inside the compartment tends to fall backward.
2. When a carpet is beaten up with a stick, the dust particles are detached.
3. When a bullet is fired into a glass pane, it pierces a hole only at the pt where the bullet hits the glass without breaking the entire glass pane into pieces.

(b) Inertia of motion: When a body is in uniform motion, it will continue to remain in its uniform motion, i.e. it resists any change in its state of motion due to inertia of motion.
Examples:
1. when a person jumps out of a moving bus, he should run in the direction in which bus is moving otherwise he will fall down.
2. A train moving with a uniform speed and if a ball is thrown upwards inside the train by a passenger, then the ball comes back to his hand.

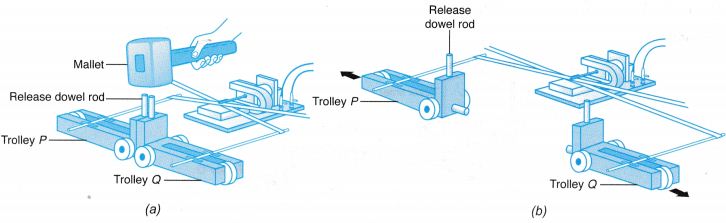
Situations involving inertia
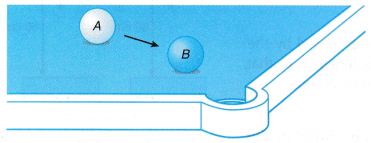
The inertia of an object is the tendency of the object to remain at rest or, if moving, to continue its uniform motion in a straight line.

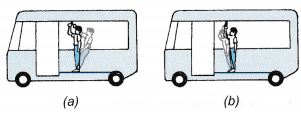Understanding inertia 3 The inertia of an object is the tendency of the object to remain at rest or, if moving, to continue its uniform motion in a straight line.
In Figure (a), when the bus moves forward suddenly, the feet of the passenger are made to move forward. The inertia of his body tends to remain at rest. Hence, the passenger falls backward.
In Figure (b), when the bus slows down suddenly, the feet of the passenger are brought to rest. The inertia of his body tends to continue moving forward. Hence, the passenger falls forward.
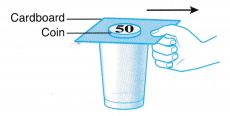Understanding inertia 4 A 50 cent coin is placed on a cardboard covering the top of a glass. After the cardboard is pulled quickly, the 50 cent coin hovers over the top of the glass for an instant before dropping into the glass. The coin hovers for an instant because of its inertia.
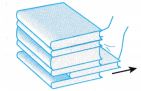Understanding inertia 5 When a book placed in the middle of a stack of books is pulled out horizontally with a quick jerk, the books above it tend to stay at rest due to inertia.
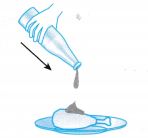Understanding inertia 6 When very little tomato sauce is left in the bottle, the bottle is given a quick downward jerk to force the sauce out of the bottle. When the bottle moves, the sauce in it moves together. When the bottle is stopped suddenly, the inertia of the sauce keeps it moving downward and out of the bottle.
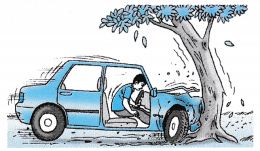Understanding inertia 7 Figure shows a driver crashing his car without wearing a safety belt. Both the driver and the car were travelling at a very high speed. When the car was stopped suddenly, the inertia of the driver caused him to be thrown forward, thus injuring himself.

Relationship between Inertia and Mass:
Larger the mass of the body, larger is the inertia.
Example: It is more difficult to stop a cricket ball than a tennis ball.

  1. The mass of an object is the amount of matter in it. The SI unit for mass is kilogram (kg). Mass is a scalar quantity.
  2. One kilogram is define’d to be the mass of a standard cylinder of a platinum-iridium alloy kept at the International Bureau of Weights and Measures in Sevres, France.

Inertia and Mass

  1. It is more difficult to move a lorry than a bicycle when both are initially at rest.
  2. When both are moving, it is also more difficult to stop the lorry than the bicycle.
  3. Hence, in comparison, the lorry has a greater tendency to be at rest than the bicycle. Likewise, the lorry has a greater tendency to continue to be in motion than the bicycle.
  4. The lorry has more inertia than the bicycle. The lorry has a bigger mass than the bicycle. Hence, quantitatively, the inertia of an object is measured by its mass.

Effects of Inertia

  • Stick
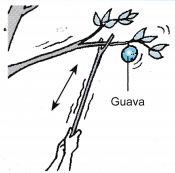
    Effects of inertia 1
    A stick is used to jerk the branch of a guava tree. At the end of the branch, there is a big guava. The guava tends to remain in its original state of rest due to its inertia. This will cause its stalk to snap and the guava will fall to the ground.
  • Tissue Paper
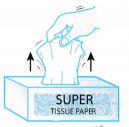
    Effects of inertia 2
    When a sheet of tissue paper is pulled quickly from a tissue box, the box will not move. The inertia of the box causes it to resist motion and remain at rest.
  • Blade of a Hoe
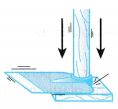
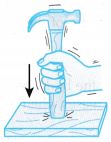
    Effects of inertia 3     Effects of inertia 4
    The blade of a hoe can be fitted tightly to its wooden handle by hitting the end of the handle against a hard surface as shown in the figure. The mass of the blade of the hoe is big and its inertia causes it to continue moving although the handle has been stopped, thus fitting it tighter to the handle. Likewise, the head of a hammer can be fitted into its handle this way too.
  • Ice Skater
    Effects of inertia 5
    After an initial push, an ice skater glides almost effortlessly on an icy surface because of inertia.
  • Safety Belt
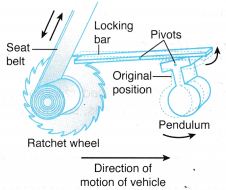
    Effects of inertia 6

    • The mechanism in a safety belt allows the belt to unwind freely when pulled gently. The mechanism consists of a ratchet wheel, a locking bar and a pendulum.
    • When the vehicle is at rest or moving with a uniform velocity, the pendulum hangs straight down with the locking bar resting horizontally on it.
    • When the vehicle is slowed down suddenly as in the case of an accident, the pendulum which has a big mass keeps moving forward due to its inertia. As a result, the pendulum swings on its pivot and causes the locking bar to block the rotation of the ratchet wheel and thus preventing the safety belt from unwinding.
  • Ship
    Effects of inertia 7
    Due to its very large mass, a ship has a very large inertia. It cannot be stopped guickly even during an emergency. A very strict navigation system is needed to guide a ship when reaching a port, sailing near rocks and icebergs as well as in busy sea routes like the Straits of Malacca to prevent accidents from happening.
  • Rear-end Collision
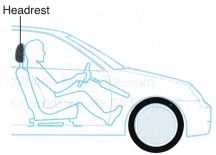
    Effects of inertia 8
    When a rear-end collision occurs, the car and the body of the driver move forward suddenly. The headrest supports the head of the driver when it is thrown backward.
  • Aeroplane
    Effects of inertia 9
    An aeroplane has a large mass. It cannot be stopped easily when it lands at airports due to its large inertia. Therefore, a very long runway is required for the aeroplane to stop safely.
  • Lorry
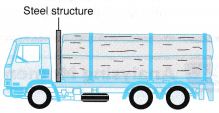
    Effects of inertia 10
    A steel structure is fitted in the space between the driver and the load of a timber lorry. This steel structure prevents any log from moving forward and knocking against the driver compartment when the lorry stops suddenly.
  • Car
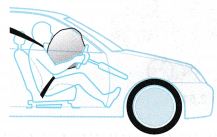
    Effects of inertia 11
    When a car stops suddenly during an accident, the driver continues to move forward because of inertia. The safety belt and airbag prevent the driver from crashing into the windscreen and injuring himself.

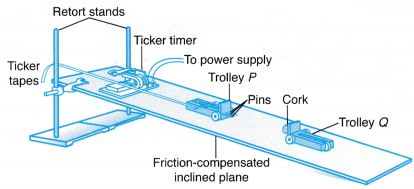
Experiment 1

Aim: To investigate the relationship between inertia and mass.
Problem: What is the relationship between inertia and mass?
Hypothesis: The inertia of a body increases when its mass increases.
Variables:
(a) Manipulated variable: Mass
(b) Responding variable: Inertia
(c) Fixed variable: Type of hacksaw blade (The same blade is used throughout the experiment)
Operational Definition: Period of oscillation is an indicator for inertia, the responding variable. The bigger the period of oscillation, the bigger is the inertia.
Material: Plasticine
Apparatus: Hacksaw blade, G-clamp, stopwatch
Method:

  1. A hacksaw blade is clamped with a G-clamp to the leg of a table as shown in Figure 2.46.
  2. A lump of plasticine with a mass of 30 g is attached to the free end of the hacksaw blade.
  3. The hacksaw blade is displaced sideways slightly and released so that it would oscillate horizontally.
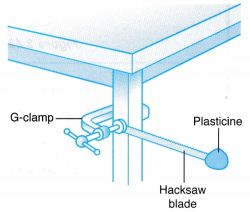
    Understanding inertia 8
  4. The time taken for 10 complete oscillations, t1 is determined using a stopwatch and recorded. This step is repeated for another reading, t2.
  5. Steps 3 and 4 are repeated with mass of plasticine, m = 40 g, 50 g, 60 g and 70 g.
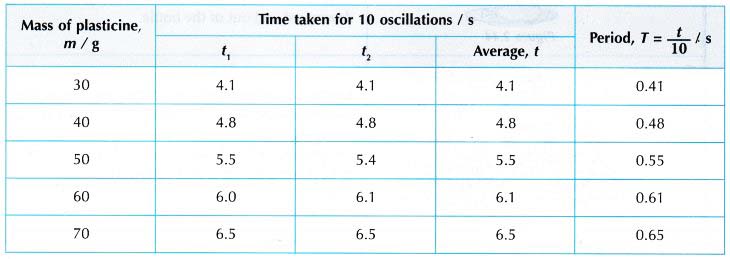
  6. The readings of t1 and t2 are recorded in Table.

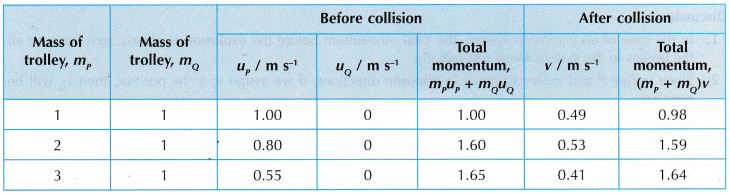
Results:
1. Tabulation of results.
Understanding inertia 9
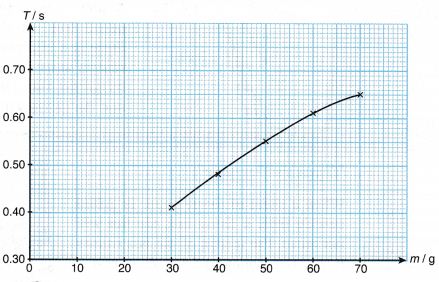
2. Graph of period, T against mass m.
Understanding inertia 10
Discussion:

  1. From the experiment, we observed that a larger mass of plasticine attached to the hacksaw blade increases the period of oscillation.
  2. The period of oscillation is an indicator of the inertia of the plasticine whereby the bigger the period of oscillation, the bigger is the inertia of the plasticine. Hence, the bigger is the mass of the plasticine, the bigger is its inertia.

Conclusion:
When the mass of a body increases, the body becomes more reluctant to change its state of rest or motion. This means that the inertia of a body increases when its mass increases.

(B) Newton’s Second Law of Motion

We know that,
Newtons second law of motion
By defining 1 newton (N) as the unit force that causes an object with a mass of 1 kg to accelerate 1 m s-2 and substituting into the equation,
1 = k (1) (1)
Therefore, k = 1
With this,
F = ma
Newton’s Second Law of Motion describes the relationship between the acceleration of an object and the force applied to it.
Newton’s second law states “the rate of change of momentum of a body is directly proportional to force and takes place in the direction of force.”
i.e., when a net external force acts on an object, the acceleration of the object is directly proportional to the net force and has a magnitude that is inversely proportional to its mass.

  • \(\text{ }F=\frac{{{P}_{2}}-{{P}_{1}}}{t}\text{    or    }F=\left( \frac{v-u}{t} \right)=m\overset{\to }{\mathop{a}}\)
    where p1 = initial momentum = mu
    p2 = final momentum = mv
  • Unit of force in SI system is newton.
  • 1N is equivalent to that force which can produce an acceleration of 1m/s5 in a body of mass 1 kg.
  • Unit of force in CGS system is dyne.
    1 dyne = 1 gm – cm/s2
    1 N = 105 dynes

Example 1. A worker pulls a block of ice on a smooth surface with a force, F. The ice has a mass of 80 kg.
Newtons second law of motion 1
(a) If the force F = 160 N, calculate the acceleration of the ice.
(b) If the velocity of the ice changes from 0 to 8 m s-2 in 5 s, calculate the force, F.
Solution:
Newtons second law of motion 2

Example 2. A hawker pushes a tank of water with a horizontal force of 45 N. The total weight of the trolley and water tank is equal to 900 N.
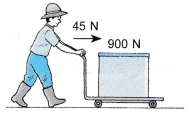
Newtons second law of motion 3
Calculate
(a) the total frictional force if the hawker moves with uniform velocity of 5 m s-1,
(b) the acceleration of the hawker if the total frictional force is equal to 30 N.
Solution:
Newtons second law of motion 4

(C) Newton’s Third Law of Motion

Newton’s first law of motion gives a qualitative idea of force, while the second law provides us an idea to measure the force.

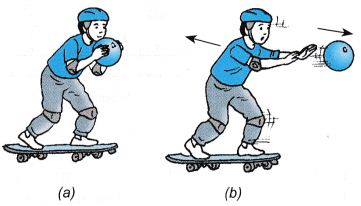
  • Newton’s third law of motion states that ” if a body A exerts a force on the body B, the body B will also exert an equal and opposite force on A.”
  • The force exerted by A on B is called action while the force exerted by B on A is called the reaction.
    Newton’s third law is also stated as “to every action there is an equal and opposite reaction.”
  • Forces always occur in pairs.
  • Action and reaction always act on different bodies.
  1. When you are practising arm wrestling with your friend, you will feel a force acting on you.
  2. Your friend will also be feeling a force acting on him. This is because while he is applying a force on you, you are also applying a force on him.
    Newtons Third law of motion 1
  3. This law is also known as the ‘action-reaction’ law. Hence, Newton’s third law of motion can be quoted as:
    ‘For every action, there is an equal but opposite reaction’.
  4. A swimmer pushes the water backward with his hands and legs with a force, F, while the reaction force of the water, -F, pushes the swimmer forward.
    Newtons Third law of motion 2
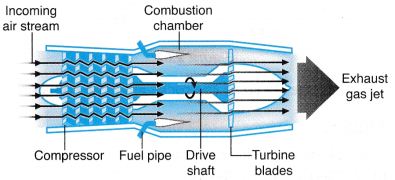
  5. Figure shows a fighter jet taking off from an airbase. The action of the exhaust gas rushing out from the nozzle with a force, F, causes a forward reaction force, -F, that moves the jet forward.
    Newtons Third law of motion 3

Applications of Newtons III law

  • Recoil of a gun: When the bullet is fired from a gun, an equal and opposite force is applied on the gun, due to which the gun recoils in backward direction.
  • Application in walking: While moving in forward direction we push the ground backwards that is the action. An equal and opposite force is applied by the ground on the man, thus the reaction due to which man moves forward.
  • Rowing a boat in river: When we push the water backward with the help of oars (applying a force backward), an equal and opposite force acts on the boat. This is the reaction which moves the boat forward.
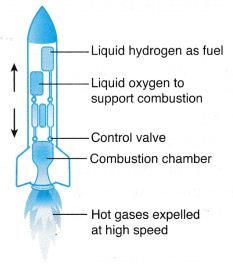
  • Launching Rocket: In rocket, gases are produced in large amount. Due to internal combustion they come out and move backwards with an equal and opposite force which in turn acts on the rocket and moves it forward.

Example 1. The diagram shows forces F1, and F2 exerted on a wooden block placed on a concrete surface. The friction between the block and the concrete surface is 3 N.
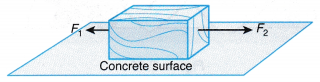
Newtons Third law of motion 4
Which pair of forces for F1, and F2 causes the wooden block to move with an acceleration?
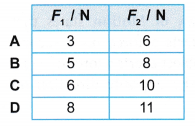
Newtons Third law of motion 5
Answer: C
Acceleration occurs when there is an unbalanced force, where the net force is not zero.

Example 2. The diagram shows a car with a mass of 850 kg moving with an acceleration of 2 m s-2. There is a frictional force of 700 N acting on the car.
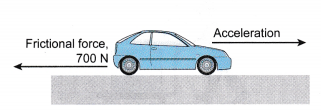
Newtons Third law of motion 6
What is the force exerted by the engine of the car?
Answer:
Force exerted by engine = (850 x 2) + 700 = 2400 N

What is Law of Conservation of Momentum

by

Law of Conservation of Momentum

  • According to law of conservation of momentum “if there is no force acting on a system, the momentum of the system remains unchanged.”
  • Generalizing the situation ” if a group of bodies are exerting force on each other, their total momentum remains conserved before and after the interaction provided there is no external force acting on them.”
    i.e. m1u1 + m2u2 = m1v1 + m2v2

 

Definition of Principle of Conservation of Momentum
The principle of conservation of momentum can also be defined as follows:

  • The total momentum in a closed system is constant.
  • A system consists of several objects acting on each other.
  • A closed system is a system where the sum of its external forces (also known as resultant force) is zero.
  • When the momentum is constant, we say the momentum is conserved.
  1. Figure shows two billiard balls, A and B. When ball A collides with ball B, ball A loses momentum and ball B gains the amount of momentum lost by ball A.
    Law of conservation momentum 14
  2. Figure (a) shows a boy standing on a skating board with a bowling ball in his hands.
    Law of conservation momentum 15
  3. When he throws the ball forward, he moves backward. Initially, the respective momentums of both the boy and the ball is zero because both are at rest.
  4. When the ball is thrown, the ball gains momentum. The boy gains an equal amount of momentum but in the opposite direction.
  5. The above observations can be explained using the principle of conservation of momentum.
  6. According to the principle of conservation of momentum, when two or more bodies act on each other, their total momentum remains constant, provided that there is no external force acting on them.

Experiment 1

Aim: To show that the total momentum of a closed system is conserved.
Problem: Is the total momentum in a closed system constant?
Hypothesis: The total momentum of a system after a collision/explosion is the same as the total momentum before the collision/explosion.
A. Collision
Materials: Cellophane tape, ticker tape, plasticine, two pins, two pieces of cork
Apparatus: Trolleys, plane, retort stands with clamps, power supply
Variables:
(a) Manipulated variable: Mass of trolley
(b) Responding variable: Velocity of trolley
Method:
Law of conservation momentum 1

  1. The apparatus is set up by attaching two pins in front of trolley P and two pieces of cork at the end of trolley Q as shown in Figure.
  2. Trolley P is placed at the higher end of the plane and trolley Q is placed halfway down the plane and is at rest. A ticker tape is passed through the ticker timer and is attached to trolley P.
  3. After the ticker timer is switched on, trolley P is given a push towards trolley Q. Both trolleys will stick together and move down the plane after the collision.
  4. The tapes are analysed to determine the following:
    (a) velocity of trolley P before the collision, up.
    (b) velocity of trolley P and trolley Q after the collision, v.
  5. Using identical trolleys, the mass of each trolley can be taken as 1 unit of mass. The experiment is repeated as follows:
    (a) two stacked trolleys collide with one trolley at rest,
    (b) three stacked trolleys collide with one trolley at rest.

Results:
Law of conservation momentum 2
Discussion:
Before collision, velocity of trolley Q, uQ = 0 because it is at rest.
Conclusion:
It is found that the total momentum after the collision is the same as that before the collision. The hypothesis is accepted.

B. Explosion
Materials: Cellophane tape, ticker tape, mallet
Apparatus: Trolleys, power supply
Variables:
(a) Manipulated variable: Mass of trolley
(b) Responding variable: Velocity of trolley
Method:
Law of conservation momentum 3

  1. Trolley P and trolley Q are set up facing each other on a smooth table as shown in Figure (a). The spring-loaded plunger of trolley P is compressed.
  2. Two ticker tapes are passed through the ticker timer, one attached to trolley P and another to trolley Q.
  3. After the ticker timer is switched on, the plunger of trolley P is released by tapping the release dowel rod with a mallet. The trolleys will ‘explode’ and move apart in opposite directions as shown in Figure (b).
  4. From the tapes obtained, the velocities of trolley P, vp and trolley Q, vQ are determined.
  5. The experiment is repeated by using two and then three stacked trolleys placed facing trolley Q.

Results:
Law of conservation momentum 4
Discussion:

  1. In the case of an explosion system, the total momentum before the explosion is always zero because all the bodies in the system are at rest initially.
  2. Since trolley P and trolley Q move in opposite directions, if we assign vP to be positive, then vQ will be negative.

Conclusion:
It is found that the total momentum before and after the explosion are the same and both are equal to zero. The hypothesis is accepted.

Applications of Conservation of Momentum

  1. (a) Figure shows the launching of a rocket. A rocket carries liquid hydrogen fuel and liquid oxygen. When a mixture of hydrogen and oxygen burns in the combustion chamber during launching, jets of hot gas are expelled at very high speed through the exhausts. This produces a very large momentum.
    Law of conservation momentum 5
    Fig. A rocket

    (b) According to the principle of conservation of momentum, an equal and opposite momentum is produced causing the rocket to propel upwards.

  2. (a) Figure shows a jet engine. Air in front of the engine is sucked into the combustion chamber by the rotating compressor blades. In the combustion chamber, fuel is injected and burnt with the compressed air.
    Law of conservation momentum 6
    Fig. A jet engine

    (b) The exploding hot jet of gases is expelled from the combustion chamber. This produces a very large momentum.
    (c) According to the principle of conservation of momentum, the expulsion of the hot gases produces an equal and opposite momentum, causing the jet plane to move forward.

  3. (a) When a bullet is fired from a submachine gun, the exploding gases from the bullet cause it to be shot out at a very high speed, producing a very big momentum.
    Law of conservation momentum 7
    Fig. A rifle

    (b) An equal and opposite momentum is produced and this causes the submachine gun to recoil.

Law of Conservation of Momentum Example Problems with Solutions

Example 1. A rifle of mass 5 kg fires a bullet of mass 40 gm. The bullet leaves the barrel of the rifle with a velocity 200 m/s. If the bullet takes 0.004 s to move through the barrel, calculate the following:
(i) recoil velocity of the rifle and
(ii) the force experienced by the rifle due to its recoil.
Solution:    (i) Given mass of the rifle, m1 = 5 kg
Mass of the bullet, m2 = 40 gm = 0.04 kg
Initial velocities, u1 = 0, u2 = 0
After firing velocity of the bullet, v2 = 200 m/s
Velocity of the rifle, v1 = ?
Applying the law of conservation of momentum, we get
m1u1 + m2u2 = m1v1 + m2v2
0 + 0 = 5 × v1 + 0.04 × 200
\({{v}_{1~}}=\frac{0.04\times 200}{5}=-1.6\text{ m/s}\)
(ii) Initial momentum of the rifle = 0
Final momentum of the rifle = 5 kg ×(–1.6)
= – 8 kg-m/s
Time interval = 0.004 s
\( \therefore \text{Force}=\frac{\text{Change}\,\text{in}\,\text{momentum}}{\text{Time}\,\text{interval}} \)
\( =\frac{-8kg-m{{s}^{-1}}}{0.004}=-2000\text{ N} \)

Example 2. A bullet of mass 20 gm moving with a velocity 200 m/s gets embedded into a wooden block of mass 980 gm suspended by a string. Calculate velocity acquired by the combined system.
Solution:    Mass of the bullet, m1 = 20 gm = 0.02 kg
Velocity of the bullet, u1 = 200 m/s
Momentum of the bullet = m1u1
= 0.02 × 200 kg-m/s = 4 kg-m/s
Now, the bullet gets embedded into a wooden block of mass 980 gm. The mass of the block and bullet = 980 + 20
= 1000 gm = 1kg
Let the velocity of the combined system = v
∴ Momentum of the combined system
= 1 × v kg-m/s = v kg-m/s
Now, applying the law of conservation of momentum,
m1u1 = (m1 + m2)v
or   4 = v
∴ v = 4 m/s = 4 kg m/s

Example 3. A rifle man, who together with his rifle has a mass of 100 kg, stands on a smooth surface fires 10 shots horizontally. Each bullet has a mass 10 gm a muzzle velocity of 800 m/s. What velocity does rifle man acquire at the end of 10 shots?
Solution:    Let m1 and m2 be the masses of bullet and the rifleman and v1 and v2 their respective velocities after the first shot. Initially the rifleman and bullet are at rest, therefore initial momentum of system = 0.
As external force is zero, momentum of system is constant
i.e. initial momentum = final momentum
= m1v1 + m2v2
\(\Rightarrow {{v}_{2}}=\frac{{{m}_{1}}{{v}_{1}}}{{{m}_{2}}}=-\frac{(10\,\times \,{{10}^{-3}}kg)(800\,m/s)}{100kg}\)
= – 0.08 m/s
Velocity acquired after 10 shots
= 10 v2 = 10 x (–0.08)
= – 0.8 m/s.
i.e, the velocity of rifle man is 0.8 m/s in a direction opposite to that of bullet.

Example 4. A body of mass 1 kg strikes elastically with another body at rest and continues to move in the same direction with one fourth of the initial velocity. What will be the mass of the other body ?
Solution:    Given that,
Initial velocity = u
Final velocity = \(\frac { u }{ 4 }\)
So by conservation of momentum, we have
1 × u + 0 = 1 × \(\frac { u }{ 4 }\) + m × v2
⇒ mv2 = \(\frac { 3u }{ 4 }\)           …(1)
and by conservation of energy, we have
\( \Rightarrow \frac{1}{2}\times 1\times {{u}^{2}}+0=~~\frac{1}{2}\times 1~{{\left( \frac{u}{4} \right)}^{2}}+~m{{v}_{2}}^{2}\)
\(\Rightarrow \text{m}{{\text{v}}_{\text{2}}}^{\text{2}}=\frac{15}{16}{{u}^{2}}\text{       }……\text{ (2)}\)
from equation (1) and (2),
\(=\frac{{{(m{{v}_{2}})}^{2}}}{mv_{2}^{2}}=\frac{(9/16){{u}^{2}}}{(15/16){{u}^{2}}}\)
or m = 0.6 kg

Example 5. Figure shows two rocks moving towards each other along a straight line. After colliding with each other, the two rocks lump together.
Calculate the speed of the rocks after the collision.
Law of conservation momentum 8
Solution:
Law of conservation momentum 9

Example 6. An astronaut with mass of 80 kg throws a 40 kg tool box in order to be able to get back to the space capsule.
If the box is thrown at a velocity of 6 m s-1, what is the velocity of the astronaut after throwing the tool box?
Law of conservation momentum 10
Solution:
Law of conservation momentum 11

Example 7. Figure shows two identical boxcars of a train being coupled at a railway station. Each boxcar has a mass of 2.5 × 104 kg. The velocities of boxcar 1 and boxcar 2 before the coupling are 1.0 m s-1 and 0.8 m s-1 respectively.
Find the velocity, v, of the boxcars after they are coupled. State one assumption in your calculation.
Law of conservation momentum 12
Solution:
Law of conservation momentum 13