Force

Selina Concise Physics Class 10 ICSE Solutions Force

by

Selina Concise Physics Class 10 ICSE Solutions Force

APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 10 Physics Chapter 1 Force. You can download the Selina Concise Physics ICSE Solutions for Class 10 with Free PDF download option. Selina Publishers Concise Physics for Class 10 ICSE Solutions all questions are solved and explained by expert teachers as per ICSE board guidelines.

Download Formulae Handbook For ICSE Class 9 and 10

ICSE SolutionsSelina ICSE Solutions

Selina ICSE Solutions for Class 10 Physics Chapter 1 Force

Exercise 1(A)

Solution 1.

(a) When the body is free to move it produces translational motion.
(b) When the body is pivoted at a point, it produces rotational motion.

Solution 2.

The moment of force is equal to the product of the magnitude of the force and the perpendicular distance of the line of action of force from the axis of rotation.
S.I. unit of moment of force is Newton metre (Nm).

Solution 3.

Moment of a force is a vector.

Solution 4.

Moment of force about a point depends on the following two factors:

  1. The magnitude of the force applied and,
  2. The distance of line of action of the force from the axis of rotation.

Solution 5.

When the body is pivoted at a point, the force applied on the body at a suitable point rotates the body about the axis passing through the pivoted point.
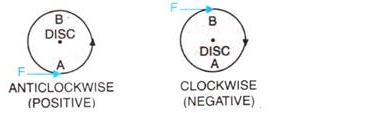
The direction of rotation can be changed by changing the point of application of force. The given figure shows the anticlockwise and clockwise moments produced in a disc pivoted at its centre by changing the point of application of force F from A to B.
Selina Concise Physics Class 10 ICSE Solutions Force 1

Solution 6.

Moment of force about a given axis = force x perpendicular distance of force from the axis of rotation.

Solution 7.

Moment of force depends on the distance of line of action of the force from the axis of rotation. Decreasing the perpendicular distance from the axis reduces the moment of a given force.

Solution 9.

If the turning effect on the body is anticlockwise, moment of force is called anticlockwise moment and it is taken as positive while if the turning effect on the body is clockwise, moment of force is called clockwise moment and is taken negative.

Solution 10.

It is easier to open a door by applying the force at the free end of it because larger the perpendicular distance , less is the force needed to turn the body.

Solution 11.

The stone of hand flour grinder is provided with a handle near its rim so that it can be rotated easily about the iron pivot at its centre by a small force applied at the handle.

Solution 12.

It is easier to turn the steering wheel of a large diameter than that of a small diameter because less force is applied on steering of large diameter which is at a large distance from the centre of rim.

Solution 13.

A spanner (or wrench) has a long handle to produce larger turning moment so that nut can easily be turned with a less force.

Solution 14.

Selina Concise Physics Class 10 ICSE Solutions Force 20

Solution 15.

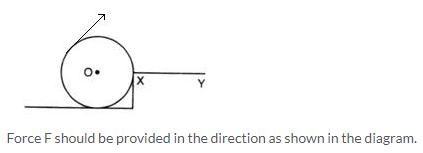
Selina Concise Physics Class 10 ICSE Solutions Force 2

Solution 16.

(a) Resultant force acting on the body = F-F=0 moment of forces = 0 i.e., no motion of the body
(b) The forces tend to rotate the body about the mid-point between two forces, Moment of forces= Fr

Solution 17.

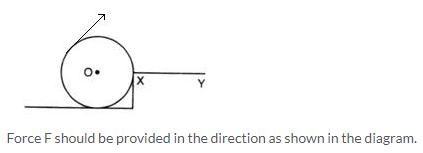
Selina Concise Physics Class 10 ICSE Solutions Force 2
At A and B, two equal and opposite forces each of magnitude F are applied. The two forces rotate the bar in anticlockwise direction.

Solution 18.

Two equal and opposite parallel forces not acting along the same line, form a couple. A couple is always needed to produce the rotation. For example, turning a key in a lock and turning a steering wheel.

Solution 19.

The moment of a couple is equal to the product of the either force and the perpendicular distance between the line of action of both the forces. S.I unit of moment of couple is Nm.

Solution 20.

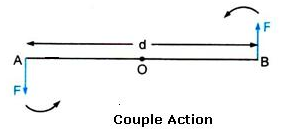
Selina Concise Physics Class 10 ICSE Solutions Force 4
At A and B, two equal and opposite forces each of magnitude F are applied. The two forces rotate the bar in anticlockwise direction. The perpendicular distance between two forces is AB which is called the couple arm.
Moment of force F at the end A
= F x OA(anticlockwise)
Moment of force F at the end B
= F x OB(anticlockwise)
Total moment of couple =F x OA + F x OB
= F x (OA +OB)= F x AB
= F x d(anticlockwise)
=Either force x perpendicular distance between the two forces (or couple arm)
Thus, Moment of couple = Force x Couple arm

Solution 21.

When a number of forces acting on a body produce no change in its state of rest or of motion, the body is said to be in equilibrium.

Solution 22.

(i) When a body remains in the state of rest under the influence of the applied forces, the body is in static equilibrium. For example a book lying on a table is in static equilibrium.
(ii) When a body remains in the same state of motion (translational or rotational), under the influence of the applied forces, the body is said to be in dynamic equilibrium. For example, a rain drop reaches the earth with a constant velocity is in dynamic equilibrium.

Solution 23.

For a body to be in equilibrium:

  1. The resultant of all the forces acting on the body should be equal to zero.
  2. The resultant moment of all the forces acting on the body about the point of rotation should be zero.

Solution 24.

According to the principle of moments, if the algebraic sum of moments of all the forces acting on the body about the axis of rotation is zero, the body is in equilibrium. A physical balance (or beam balance) works on the principle of moments.

Solution 25.

Selina Concise Physics Class 10 ICSE Solutions Force 5

Solution 1 (MCQ).

The moment of a force about a given axis depends on both on the force and its perpendicular distance from the axis.
Hint: Moment of force = Force x Perpendicular distance

Solution 2 (MCQ).

The body will have rotational as well as translational motion.

Numericals

Solution 1.

Moment of force= force x perpendicular distance of force from point O
Moment of force= F x r
5Nm= 10 x r
R= 5/10 =0.5 m

Solution 2.

Length, r=10cm =0.1m
F= 5N
Moment of force= F x r= 5 x 0.1 = 0.5 Nm

Solution 3.

Given , F= 2N
Diameter=2m
Perpendicular distance between B and O =1m
(i)Moment of force at point O
= F x r
= 2 x 1=2Nm (clockwise)
(ii)Moment of force at point A= F x r
= 2 x 2=4Nm (clockwise)

Solution 4.

Given AO=2m and OB=4m

(i) Moment of force F1(=5N) at A about the point O
=F1 x OA
=5 x 2= 10Nm (anticlockwise)

(ii) Moment of force F2(=3N) at B about the point O
= F2 x OB
=3 x 4=12 Nm(clockwise)

(iii) Total moment of forces about the mid-point O
= 12- 10=2Nm(clockwise)

Solution 5.

Given, AB=4m hence, OA=2m and OB =2m
Moment of force F(=10N) at A about the point O
= F x OA= 10 x 2= 20Nm (clockwise)
Moment of force F (=10N) at point B about the point O
= F x OB= 10 x 2 =20Nm (clockwise)
Total moment of forces about the mid-point O=
=20 +20= 40Nm(clockwise)

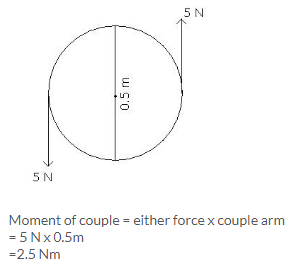
Solution 6.

(i) Perpendicular distance of point A from the force F=10 N at B is 0.5m , while it is zero from the force F=10N at A
Hence, moment of force about A is
= 10 N x 0.5m=5Nm(clockwise)

(ii) Perpendicular distance of point B from the force F=10 N at A is 0.5m, while it is zero from the force F=10N at B
Hence, moment of force about B is
= 10 N x 0.5m=5Nm(clockwise)

(iii) Perpendicular distance of point O from either of the forces F=10N is 0.25 m
Moment of force F(=10N) at A about O= 10N x 0.25m
=2.5Nm(clockwise)
And moment of force F(=10N) at B about O
=10N x 0.25m=2.5Nm(clockwise)
Hence, total moment of the two forces about O
=0.25 + 0.25=5Nm (clockwise)

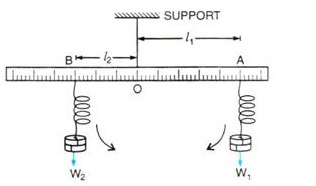
Solution 7.
Selina Concise Physics Class 10 ICSE Solutions Force 6

Solution 8.
Let the 50gf weight produce anticlockwise moment about the middle point of metre rule .i.e, at 50cm.
Let a weight of 100gf produce a clockwise moment about the middle point. Let its distance from the middle be d cm. Then,
according to principle of moments,
Anticlockwise moment = Clockwise moment
50gf x 50 cm=100gf x d
Selina Concise Physics Class 10 ICSE Solutions Force 21

Solution 9.

(i) Weight mg (W) of rule produces an anti-clockwise moment about the knife edge O. In order to balance it, 20gf must be suspended at the end B to produce clockwise moment about the knife edge O.
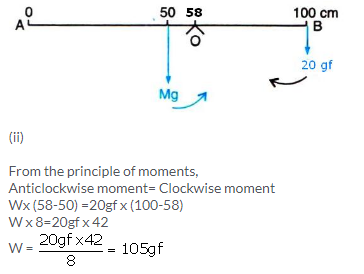
Selina Concise Physics Class 10 ICSE Solutions Force 7

Solution 10.

Anticlockwise moment= 40gf x 40 cm
Clockwise moment= 80gf x d cm
From the principle of moments,
Anticlockwise moment= Clockwise moment
40gf x 40 cm =80gf x d
Selina Concise Physics Class 10 ICSE Solutions Force 8

Solution 11.

(i) Anticlockwise moment= 40gf x (50-10)cm
=40gf x 40cm=1600 gf x cm
Clockwise moment= 20gf x (90- 50) =20gf x 40cm
=800 gf x cm
Anticlockwise moment is not equal to clockwise moment. Hence the metre rule is not in equilibrium and it will turn anticlockwise.

(ii) To balance it, 40gf weight should be kept on right hand side so as to produce a clockwise moment about the middle point. Let its distance from the middle be d cm. Then,
clockwise moment= 20gf x 40cm + 40gf x d cm
From the principle of moments,
Anticlockwise moment= Clockwise moment
40 gf x 40 cm= 20gf x 40 + 40 x d cm
1600-800=40gf x dcm
Selina Concise Physics Class 10 ICSE Solutions Force 9

Solution 12.

From the principle of moments,
Anticlockwise moment= Clockwise moment
20kgf x 2m =40kgf x d
Selina Concise Physics Class 10 ICSE Solutions Force 10

Solution 13.
Selina Concise Physics Class 10 ICSE Solutions Force 11

Solution 14.

(i) Total anticlockwise moment about O
= 150gf x 40 cm=6000gf cm

(ii) Total clockwise moment about O,
=250gf x 20 cm= 5000gf cm

(iii) The difference of anticlockwise and clockwise moment= 6000- 5000= 1000gf cm

(iv) From the principle of moments,
Anticlockwise moment= Clockwise moment
To balance it, 100gf weight should be kept on right hand side so as to produce a clockwise moment about the O. Let its distance from the point O be d cm. Then,
150gf x 40 cm=250gf x 20 cm +100gf x d
6000gf cm= 5000gf cm + 100gf x d
1000gf cm =100 gf x d
Selina Concise Physics Class 10 ICSE Solutions Force 12

Solution 15.
Selina Concise Physics Class 10 ICSE Solutions Force 13

Solution 16.
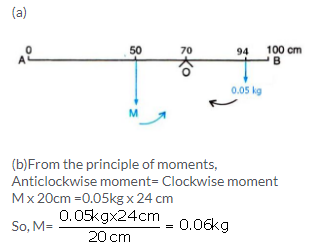
Selina Concise Physics Class 10 ICSE Solutions Force 14

Solution 17.

(i) From the principle of moments,
Clockwise moment= Anticlockwise moment
100g x (50-40) cm= mx(40-20) cm
100g x 10 cm = m x 20 cm = m =50 g

(ii) The rule will tilt on the side of mass m (anticlockwise), if the mass m is moved to the mark 10cm.

(iii) Anticlockwise moment if mass m is moved to the mark 10 cm= 50g x (40-10)cm =50 x 30=1500g cm
Clockwise moment=100g x (50-40) cm= 1000g cm
Resultant moment= 1500g cm -1000g cm= 500g cm (anticlockwise)

(iv) From the principle of moments,
Clockwise moment= Anticlockwise moment
To balance it, 50g weight should be kept on right hand side so as to produce a clockwise moment .Let its distance from fulcrum be d cm. Then,
100g x (50-40) cm + 50g x d =50g x (40-10)cm
1000g cm + 50g x d =1500 g cm
50 g x d= 500g cm
So, d =10 cm
By suspending the mass 50g at the mark 50 cm, it can be balanced.

Exercise 1(B)

Solution 1.

Centre of gravity is the point about which the algebraic sum of moments of weights of particles constituting the body is zero and the entire weight of the body is considered to act at this point.

Solution 2.

Yes, the centre of gravity can be situated outside the material of the body. For example, centre of gravity of ring.

Solution 3.

The position of centre of gravity of a body of given mass depends on its shape i.e., on the distribution of mass in it. For example: the centre of gravity of a uniform wire is at its mid-point. But if this wire is bent into the form of a circle, its centre of gravity will then be at the centre of circle.

Solution 4.

The position of centre of gravity of a
(a) rectangular lamina is at the point of intersection of its diagonals.
(b) cylinder is at the mid point on the axis of cylinder.

Solution 5.

(a) Centre of gravity of a triangular lamina is situated at the point of intersection of its medians.
(b) Centre of gravity of a circular lamina is situated at the centre of circular lamina.

Solution 6.

Centre of gravity of a uniform ring is situated at the centre of ring.

Solution 7.
Selina Concise Physics Class 10 ICSE Solutions Force 15

Solution 8.

Take a triangular lamina. Make three fine holes at a, b, c near the edge of triangular lamina. Now suspend the given lamina along with a plumb line from hole ‘a’. Check that the lamina is free to oscillate about the point of suspension. When lamina has come to rest, draw straight line ad along the plumb line. Repeat the experiment by suspending the lamina through hole ‘b’ and then through hole ‘c’ for which we get straight lines be and cf respectively. It is noticed that the lines ad, be and cf intersect each other at a common point G which is the position of centre of gravity of triangular lamina i.e. the point of intersection of medians.
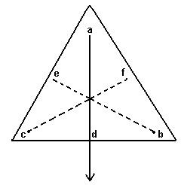
Selina Concise Physics Class 10 ICSE Solutions Force 16

Solution 9.

(i) False. The position of centre of gravity of a body of given mass depends on its shape i.e., on the distribution of mass in it.
(ii) True.

Solution 10.
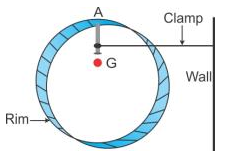
Selina Concise Physics Class 10 ICSE Solutions Force 17

Solution 11.
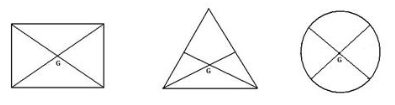
Selina Concise Physics Class 10 ICSE Solutions Force 18

Solution 1 (MCQ).

At its geometrical centre

Exercise 1(C)

Solution 1.

When a particle moves with a constant speed in a circular path, its motion is said to be the uniform circular motion. For example : Revolution of earth around sun is an example of uniform circular motion.

Solution 2.

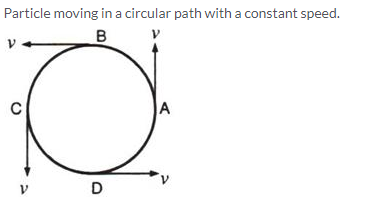
Selina Concise Physics Class 10 ICSE Solutions Force 19

Solution 3.

Yes, uniform circular motion has an accelerated motion with a constant speed.

Solution 4.

Motion of a cyclist on a circular track is an example of motion in which speed remains uniform, but the velocity changes.

Solution 5.

When the object moves in a circular path with uniform speed, it means that its magnitude of velocity does not change, only its direction changes continuously. Hence, it is considered as uniformly accelerated motion.

Solution 6.

Uniform linear motionUniform circular motion
The body moves along a straight line.The body moves along a circular path.
Speed and direction both remain constant.Speed is constant, but direction changes continuously.
It is not an accelerated motion.It is an accelerated motion.

Solution 7.

Centripetal force is required for circular motion. It is always directed towards the centre of circle.

Solution 8.

Force acting on a body which is in circular motion is called centripetal force. It acts towards the centre of circular path.

Solution 9.

A planet moves around the sun in a nearly circular path for which the gravitational force of attraction on the planet by the sun provides the necessary centripetal force required for circular motion.

Solution 10.

(a) They act in opposite directions.
(b) No, centrifugal force is not the force of reaction of centripetal force.

Solution 11.

No, centrifugal force is a fictitious force.

Solution 12.

a. On standing outside the disc, we find that the pebble is moving on a circular path. On standing at the centre of the disc, we find that the pebble is stationary placed just in front of us.

Solution 13.

Force of tension in the thread provides the centripetal force.

Solution 15.

(a) False
(b) True
(c) True
(d) False

Solution 1 (MCQ).

Speed
Hint: Speed is scalar but velocity and acceleration are vector quantities. So, speed remains constant but velocity and acceleration change with the change in direction, and in circular motion the direction of motion changes at every point.

More Resources for Selina Concise Class 10 ICSE Solutions

What Are The Examples Of Contact Forces

by

Examples Of Contact Forces

Forces that act on objects by direct or indirect physical contact are called contact forces. Applied forces and friction are examples of contact forces.

Applied Forces
The forces that we use with our hands, legs, fingers, etc., are collectively called appliedforces. When we tie a stone to a string and suspend it, the tension in the string opposes the force of gravity of the Earth and keeps the stone from falling down. When we do work with our hands, like lifting a weight, or pulling an object, the force required is provided by the tension of our muscles. When we need to apply a force, the brain sends a signal to the muscle (in the form of electrical signals via the nerve cells), which makes the muscle contract. This is how we can apply a force with our hands, legs, etc.

Friction
The resistance to motion experienced when two surfaces in contact move with respect to each other is calledfriction. Whenever the surface of one body slides over that of another, each exerts a force on the other which opposes the motion of the body. This is called frictional force. Frictional force comes into play only when two surfaces are in physical contact and is, therefore, a contact force. Friction is a very complex phenomenon, and there is a lot about it that still needs to be explained. Two simple explanations for why friction is caused are as follows:

  • Any surface, however smooth, has a lot of irregularities when seen under a microscope. These irregularities are like hills and valleys. When two such surfaces slide over each other, there will be a resistance to motion (friction).
  • Another theory that explains friction says that when two surfaces come in contact, their atoms and molecules pull each other due to electrostatic forces. They ‘stick’ to each other at a microscopic level. When we try to slide the surfaces with respect to each other, these offer a resistance to motion. Frictional force depends on two main factors: the nature of the surfaces in contact and the mass of the object.

Activity

Aim: To show that frictional force depends on the nature of the two surfaces in contact.
Materials needed: A few books, plastic sheet, nylon cloth, gunny cloth, jute cloth, sandpaper, thread, and spring balance.
Method:

  1. Make a stack of books and, with the help of a thread, wrap the materials around it one by one, as shown in figure.
  2. Attach this stack to a spring balance, as shown in the figure, and pull gently.
  3. Note the reading on the spring balance.

What Are The Examples Of Contact Forces 1

Observation: You will notice that different materials offer different amounts of resistance (friction) to sliding. You will see from this activity that the force of friction depends on the nature of the surfaces in contact.
Conclusion: In general, smooth surfaces offer lesser friction than rough surfaces. The reading on the spring balance will be higher for rougher surfaces.

Aim: To study the effect of mass of a body on friction.
Materials needed: A 100/200 page notebook and two or three thick books (small enough so that they can be placed on the notebook).
Method:

  1. Place the notebook on the floor, and push the notebook gently on the floor (figure 1). Make a mental note of the resistance (friction) offered to your pushing the notebook.
  2. Place one thick book on the notebook and repeat step 1 (figure 2).
  3. Keep increasing the number of books and repeat step 1 (figure 3).

What Are The Examples Of Contact Forces 2

Observation: As you increase the number of books on your notebook, you will see that the frictional force increases. The area of contact and the nature of the surfaces (notebook and floor) remain the same.
Conciusion: Frictional force increases as mass increases.

Sliding and Rolling Friction
Generally, sliding an object (like a cylinder) is more difficult than rolling it. The frictional force offered when sliding an object is called sliding friction, and that offered when rolling an object is called rolling friction. The fact that rolling friction is smaller than sliding friction is made use of in a device called ball bearing.

Activity 

Aim: To show that rolling friction is less than sliding friction.
Materials needed: Two wooden examination pads/planks and 4-6 pencils of equal size and round sides (or 4-6 small marbles of equal size).
Method:

  1. Place one of the examination pads upside down on a table top. Place it at the edge of the table so that the clip juts out. Ensure that the pad is absolutely flat on the table.
  2. Place the second examination pad (with the clip facing upward). Make sure that the two examination pads are touching each other back to back.
  3. Slide one pad over the other. Make a mental note of the friction offered.
  4. Place the pencils/marbles between the two back surfaces of the pads, and slide one pad over the other. Notice the friction offered.
  5. Compare the friction encountered in steps 3 and 4. What do you conclude?

What Are The Examples Of Contact Forces 3
Observation: You will notice that if pencils or marbles are placed between the two pad surfaces, the friction offered is much less. This is because the pencils/marbles roll as the pads slide across each other.
Conclusion: Rolling friction is less than sliding friction.

What Are The Examples Of Non Contact Forces

by

Examples Of Non Contact Forces

Forces that do not need physical contact with the object on which they are acting are called non-contact forces. Gravitational force, electrostatic force, and magnetic force are examples of non-contact forces.

Gravitational Force
The force with which objects pull each other is called gravitational force. This force is very small and we can feel it only if an object is very massive, like the Earth. It is the gravitational force of the Earth that keeps us bound to the Earth. Gravitational force makes the Earth move around the sun and also makes the moon go around the Earth. In fact, our weight is the gravitational force of the Earth acting on us. Different objects exert different magnitudes of gravitational force. For example, the gravitational force of the moon is about one-sixth that of the Earth. This means that the weight of any object on the moon will be one-sixth of its weight on the Earth.

Electrostatic Force
The force between electric charges is called electrostatic force. If we rub a plastic object like a pen, comb, or CD with hair and bring it close to tiny bits of paper, the bits of paper get attracted to the plastic objec. This is due to electrostatic force. Tiny particles of dust and smoke can also be attracted by electrostatic force. This method is used in electric air purifiers and in factories to purify air in chimneys before letting it escape into the atmosphere.
What Are The Examples Of Non Contact Forces 1

Magnetic Force
The force exerted by magnets on each other and on metals like iron and nickel is called magnetic force. Since magnets attract iron, they are used to separate waste iron objects from garbage dumps so that they can be recycled.
What Are The Examples Of Non Contact Forces 2

Newton’s Laws Of Motion

by

Newton’s Laws Of Motion

(A) Newton’s First Law of Motion

A body can not change its state of motion by itself. If the object is at rest it will remain at rest and if it is in uniform motion, it continues to be in motion unless some external force is applied on it.

  1. Newton’s First Law of Motion states that if there is no net force acting on a body, its state of motion will be unchanged.
  2. If the body is at rest, it will remain at rest. If the body is moving, it keeps on moving at a constant speed in a straight line.
  3. Newton’s first law is sometimes called the Law of Inertia.
  4. The object is not necessarily at rest. The object may be moving at constant speed in a straight line.
  5. To remember Newton’s First Law of Motion
    When F = 0 (No resultant force)
    Understanding inertia 1
    Understanding inertia 2

Inertia:
There is an inherent property of an object by virtue of which it cannot change its state of motion or rest by itself. This property is called ‘inertia’.
Inertia is of two types– inertia of rest and inertia of motion.

(a) Inertia of rest: If the body is at rest, it will continue to be at rest unless some external force is applied on it. Examples are following.
Examples:
1. When a train at rest starts moving suddenly, a passenger standing inside the compartment tends to fall backward.
2. When a carpet is beaten up with a stick, the dust particles are detached.
3. When a bullet is fired into a glass pane, it pierces a hole only at the pt where the bullet hits the glass without breaking the entire glass pane into pieces.

(b) Inertia of motion: When a body is in uniform motion, it will continue to remain in its uniform motion, i.e. it resists any change in its state of motion due to inertia of motion.
Examples:
1. when a person jumps out of a moving bus, he should run in the direction in which bus is moving otherwise he will fall down.
2. A train moving with a uniform speed and if a ball is thrown upwards inside the train by a passenger, then the ball comes back to his hand.

Situations involving inertia
The inertia of an object is the tendency of the object to remain at rest or, if moving, to continue its uniform motion in a straight line.

Understanding inertia 3 The inertia of an object is the tendency of the object to remain at rest or, if moving, to continue its uniform motion in a straight line.
In Figure (a), when the bus moves forward suddenly, the feet of the passenger are made to move forward. The inertia of his body tends to remain at rest. Hence, the passenger falls backward.
In Figure (b), when the bus slows down suddenly, the feet of the passenger are brought to rest. The inertia of his body tends to continue moving forward. Hence, the passenger falls forward.
Understanding inertia 4 A 50 cent coin is placed on a cardboard covering the top of a glass. After the cardboard is pulled quickly, the 50 cent coin hovers over the top of the glass for an instant before dropping into the glass. The coin hovers for an instant because of its inertia.
Understanding inertia 5 When a book placed in the middle of a stack of books is pulled out horizontally with a quick jerk, the books above it tend to stay at rest due to inertia.
Understanding inertia 6 When very little tomato sauce is left in the bottle, the bottle is given a quick downward jerk to force the sauce out of the bottle. When the bottle moves, the sauce in it moves together. When the bottle is stopped suddenly, the inertia of the sauce keeps it moving downward and out of the bottle.
Understanding inertia 7 Figure shows a driver crashing his car without wearing a safety belt. Both the driver and the car were travelling at a very high speed. When the car was stopped suddenly, the inertia of the driver caused him to be thrown forward, thus injuring himself.

Relationship between Inertia and Mass:
Larger the mass of the body, larger is the inertia.
Example: It is more difficult to stop a cricket ball than a tennis ball.

  1. The mass of an object is the amount of matter in it. The SI unit for mass is kilogram (kg). Mass is a scalar quantity.
  2. One kilogram is define’d to be the mass of a standard cylinder of a platinum-iridium alloy kept at the International Bureau of Weights and Measures in Sevres, France.

Inertia and Mass

  1. It is more difficult to move a lorry than a bicycle when both are initially at rest.
  2. When both are moving, it is also more difficult to stop the lorry than the bicycle.
  3. Hence, in comparison, the lorry has a greater tendency to be at rest than the bicycle. Likewise, the lorry has a greater tendency to continue to be in motion than the bicycle.
  4. The lorry has more inertia than the bicycle. The lorry has a bigger mass than the bicycle. Hence, quantitatively, the inertia of an object is measured by its mass.

Effects of Inertia

  • Stick
    Effects of inertia 1
    A stick is used to jerk the branch of a guava tree. At the end of the branch, there is a big guava. The guava tends to remain in its original state of rest due to its inertia. This will cause its stalk to snap and the guava will fall to the ground.
  • Tissue Paper
    Effects of inertia 2
    When a sheet of tissue paper is pulled quickly from a tissue box, the box will not move. The inertia of the box causes it to resist motion and remain at rest.
  • Blade of a Hoe
    Effects of inertia 3     Effects of inertia 4
    The blade of a hoe can be fitted tightly to its wooden handle by hitting the end of the handle against a hard surface as shown in the figure. The mass of the blade of the hoe is big and its inertia causes it to continue moving although the handle has been stopped, thus fitting it tighter to the handle. Likewise, the head of a hammer can be fitted into its handle this way too.
  • Ice Skater
    Effects of inertia 5
    After an initial push, an ice skater glides almost effortlessly on an icy surface because of inertia.
  • Safety Belt
    Effects of inertia 6

    • The mechanism in a safety belt allows the belt to unwind freely when pulled gently. The mechanism consists of a ratchet wheel, a locking bar and a pendulum.
    • When the vehicle is at rest or moving with a uniform velocity, the pendulum hangs straight down with the locking bar resting horizontally on it.
    • When the vehicle is slowed down suddenly as in the case of an accident, the pendulum which has a big mass keeps moving forward due to its inertia. As a result, the pendulum swings on its pivot and causes the locking bar to block the rotation of the ratchet wheel and thus preventing the safety belt from unwinding.
  • Ship
    Effects of inertia 7
    Due to its very large mass, a ship has a very large inertia. It cannot be stopped guickly even during an emergency. A very strict navigation system is needed to guide a ship when reaching a port, sailing near rocks and icebergs as well as in busy sea routes like the Straits of Malacca to prevent accidents from happening.
  • Rear-end Collision
    Effects of inertia 8
    When a rear-end collision occurs, the car and the body of the driver move forward suddenly. The headrest supports the head of the driver when it is thrown backward.
  • Aeroplane
    Effects of inertia 9
    An aeroplane has a large mass. It cannot be stopped easily when it lands at airports due to its large inertia. Therefore, a very long runway is required for the aeroplane to stop safely.
  • Lorry
    Effects of inertia 10
    A steel structure is fitted in the space between the driver and the load of a timber lorry. This steel structure prevents any log from moving forward and knocking against the driver compartment when the lorry stops suddenly.
  • Car
    Effects of inertia 11
    When a car stops suddenly during an accident, the driver continues to move forward because of inertia. The safety belt and airbag prevent the driver from crashing into the windscreen and injuring himself.

Experiment 1

Aim: To investigate the relationship between inertia and mass.
Problem: What is the relationship between inertia and mass?
Hypothesis: The inertia of a body increases when its mass increases.
Variables:
(a) Manipulated variable: Mass
(b) Responding variable: Inertia
(c) Fixed variable: Type of hacksaw blade (The same blade is used throughout the experiment)
Operational Definition: Period of oscillation is an indicator for inertia, the responding variable. The bigger the period of oscillation, the bigger is the inertia.
Material: Plasticine
Apparatus: Hacksaw blade, G-clamp, stopwatch
Method:

  1. A hacksaw blade is clamped with a G-clamp to the leg of a table as shown in Figure 2.46.
  2. A lump of plasticine with a mass of 30 g is attached to the free end of the hacksaw blade.
  3. The hacksaw blade is displaced sideways slightly and released so that it would oscillate horizontally.
    Understanding inertia 8
  4. The time taken for 10 complete oscillations, t1 is determined using a stopwatch and recorded. This step is repeated for another reading, t2.
  5. Steps 3 and 4 are repeated with mass of plasticine, m = 40 g, 50 g, 60 g and 70 g.
  6. The readings of t1 and t2 are recorded in Table.

Results:
1. Tabulation of results.
Understanding inertia 9
2. Graph of period, T against mass m.
Understanding inertia 10
Discussion:

  1. From the experiment, we observed that a larger mass of plasticine attached to the hacksaw blade increases the period of oscillation.
  2. The period of oscillation is an indicator of the inertia of the plasticine whereby the bigger the period of oscillation, the bigger is the inertia of the plasticine. Hence, the bigger is the mass of the plasticine, the bigger is its inertia.

Conclusion:
When the mass of a body increases, the body becomes more reluctant to change its state of rest or motion. This means that the inertia of a body increases when its mass increases.

(B) Newton’s Second Law of Motion

We know that,
Newtons second law of motion
By defining 1 newton (N) as the unit force that causes an object with a mass of 1 kg to accelerate 1 m s-2 and substituting into the equation,
1 = k (1) (1)
Therefore, k = 1
With this,
F = ma
Newton’s Second Law of Motion describes the relationship between the acceleration of an object and the force applied to it.
Newton’s second law states “the rate of change of momentum of a body is directly proportional to force and takes place in the direction of force.”
i.e., when a net external force acts on an object, the acceleration of the object is directly proportional to the net force and has a magnitude that is inversely proportional to its mass.

  • \(\text{ }F=\frac{{{P}_{2}}-{{P}_{1}}}{t}\text{    or    }F=\left( \frac{v-u}{t} \right)=m\overset{\to }{\mathop{a}}\)
    where p1 = initial momentum = mu
    p2 = final momentum = mv
  • Unit of force in SI system is newton.
  • 1N is equivalent to that force which can produce an acceleration of 1m/s5 in a body of mass 1 kg.
  • Unit of force in CGS system is dyne.
    1 dyne = 1 gm – cm/s2
    1 N = 105 dynes

Example 1. A worker pulls a block of ice on a smooth surface with a force, F. The ice has a mass of 80 kg.
Newtons second law of motion 1
(a) If the force F = 160 N, calculate the acceleration of the ice.
(b) If the velocity of the ice changes from 0 to 8 m s-2 in 5 s, calculate the force, F.
Solution:
Newtons second law of motion 2

Example 2. A hawker pushes a tank of water with a horizontal force of 45 N. The total weight of the trolley and water tank is equal to 900 N.
Newtons second law of motion 3
Calculate
(a) the total frictional force if the hawker moves with uniform velocity of 5 m s-1,
(b) the acceleration of the hawker if the total frictional force is equal to 30 N.
Solution:
Newtons second law of motion 4

(C) Newton’s Third Law of Motion

Newton’s first law of motion gives a qualitative idea of force, while the second law provides us an idea to measure the force.

  • Newton’s third law of motion states that ” if a body A exerts a force on the body B, the body B will also exert an equal and opposite force on A.”
  • The force exerted by A on B is called action while the force exerted by B on A is called the reaction.
    Newton’s third law is also stated as “to every action there is an equal and opposite reaction.”
  • Forces always occur in pairs.
  • Action and reaction always act on different bodies.
  1. When you are practising arm wrestling with your friend, you will feel a force acting on you.
  2. Your friend will also be feeling a force acting on him. This is because while he is applying a force on you, you are also applying a force on him.
    Newtons Third law of motion 1
  3. This law is also known as the ‘action-reaction’ law. Hence, Newton’s third law of motion can be quoted as:
    ‘For every action, there is an equal but opposite reaction’.
  4. A swimmer pushes the water backward with his hands and legs with a force, F, while the reaction force of the water, -F, pushes the swimmer forward.
    Newtons Third law of motion 2
  5. Figure shows a fighter jet taking off from an airbase. The action of the exhaust gas rushing out from the nozzle with a force, F, causes a forward reaction force, -F, that moves the jet forward.
    Newtons Third law of motion 3

Applications of Newtons III law

  • Recoil of a gun: When the bullet is fired from a gun, an equal and opposite force is applied on the gun, due to which the gun recoils in backward direction.
  • Application in walking: While moving in forward direction we push the ground backwards that is the action. An equal and opposite force is applied by the ground on the man, thus the reaction due to which man moves forward.
  • Rowing a boat in river: When we push the water backward with the help of oars (applying a force backward), an equal and opposite force acts on the boat. This is the reaction which moves the boat forward.
  • Launching Rocket: In rocket, gases are produced in large amount. Due to internal combustion they come out and move backwards with an equal and opposite force which in turn acts on the rocket and moves it forward.

Example 1. The diagram shows forces F1, and F2 exerted on a wooden block placed on a concrete surface. The friction between the block and the concrete surface is 3 N.
Newtons Third law of motion 4
Which pair of forces for F1, and F2 causes the wooden block to move with an acceleration?
Newtons Third law of motion 5
Answer: C
Acceleration occurs when there is an unbalanced force, where the net force is not zero.

Example 2. The diagram shows a car with a mass of 850 kg moving with an acceleration of 2 m s-2. There is a frictional force of 700 N acting on the car.
Newtons Third law of motion 6
What is the force exerted by the engine of the car?
Answer:
Force exerted by engine = (850 x 2) + 700 = 2400 N

How Do You Find Buoyant Force

by

How Do You Find Buoyant Force

Buoyancy
When a body is immersed in a liquid, the liquid exerts an upward force on the body called as the ‘upthrust‘ or ‘buoyant force.’

Factors affecting upthrust:
1. Larger the volume of the body submerged in the liquid, greater is the upthrust.
2. Larger the density of the liquid, greater is the upthrust.

Applying Archimedes’ Principle

Figure shows a boy transferring a boulder from the seabed to a beach.

(a) He finds that the boulder becomes heavier as it emerges from the surface of the sea.
(b) The boulder is lighter when it is immersed in the sea because of the existence of the buoyant force.
(c) The buoyant force is an upward force resulting from an object being wholly or partially immersed in a fluid.
(d) The bigger the volume of the boulder immersed in the sea, the bigger the buoyant force.
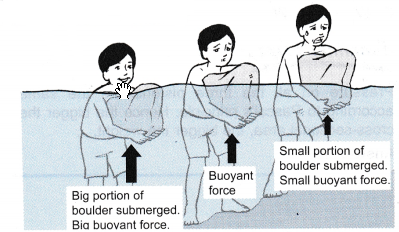
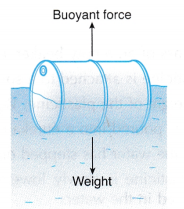
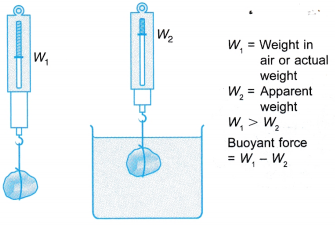Applying Archimedes' Principle 1Figure shows the relationship between real weight and apparent weight of an object and the upward buoyant force acting on it.
Buoyant force = Actual weight – Apparent weight
Therefore,
Apparent weight = Actual weight – Buoyant force

Experiment:

Aim: To investigate the relationship between the weight of water displaced and the buoyant force.
Situation: A hawker immersed a watermelon into a tub filled with water. Water was displaced from the tub when the watermelon was submerged in it. He noticed that the submerged watermelon was lighter.
Applying Archimedes' Principle 5Problem: What is the relationship between the weight of water displaced and the buoyant force?
Materials: Plasticine, thread
Apparatus: Spring balance, electronic balance, eureka can, beaker
Method:
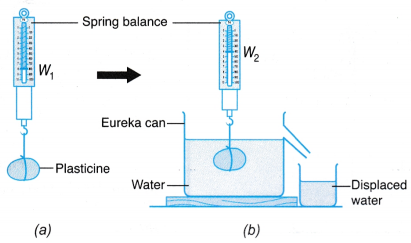
Applying Archimedes' Principle 6

  1. The mass of an empty beaker, m, is measured with an electronic balance and recorded.
  2. A plasticine is attached to a spring balance with a string as shown in Figure (a).
  3. The weight of the plasticine, W1 is measured and recorded.
  4. Water is poured into a eureka can until it flows out of the spout of the can.
  5. When the water has stopped dripping from the spout, the empty beaker is placed under it.
  6. The plasticine is slowly lowered into the eureka can as shown in Figure (b) until it is completely immersed in the water.
  7. The readings of the spring balance, W2 and the mass of the beaker that is filled with displaced water, m2 are taken and recorded.

Results:
Applying Archimedes' Principle 7
Discussion:
From the experiment, it is found that (m2 – m1) g = (W1 – W2).
Hence, the weight of water displaced is equal to the buoyant force.

Buoyant Force Example Problems with Solutions

Example 1. A body weighs 300 gmf in air and 260 gmf when completely immersed in water. Calculate the following
(i) loss in weight of the body
(ii) upthrust on the body.
Solution:    Given: Weight of body in air = 300 gmf
Weight of the body in water = 260 gmf
∴ Loss in weight of the body = 300 – 260 = 40 gmf
∴ Upthrust of the body = Loss in weight
= 40 gmf

Example 2. A solid block of volume 2 litres has a weight of 80 N. What will be its weight when immersed completely in water ?
Solution:     In order to calculate the weight of the block in water, first calculate the upthrust, i.e. the loss in weight of the body in water, then
Volume of the block = 2 litres = 2000 cc
∴ Volume of water displaced = 2000 cc
Weight of water displaced = 2000 gm
= 2.0 kgf
( Density of water = 1 gm/cc)
= 2.0 × 9.8 N = 19.6 N
∴ Upthrust of water = 19.6 N
Hence, weight of the body fully immersed in water = 80 N – 19.6 N = 60.4 N

Example 3. A solid block of density D has a weight W in air is fully immersed in a liquid of density d. Calculate its apparent weight when fully immersed in liquid.
Solution:    Weight of the block = W
Density of block = D
∴ Volume of the block = \(\frac { W }{ D }\) . d
∴ Upthrust on the block = \(\frac { W }{ D }\) .d
∴ Loss in weight of the block inside liquid = \(\frac { W }{ D }\) .d
Hence, apparent weight of the block when fully immersed in water
\(=\text{W}-\frac{\text{W}}{\text{D}}\text{d}=\text{W}\left( 1-\frac{\text{d}}{\text{D}} \right)\)

Example 4. The weight of a stone in air is 0.65 N. When it is completely submerged in water, its weight is 0.50 N.
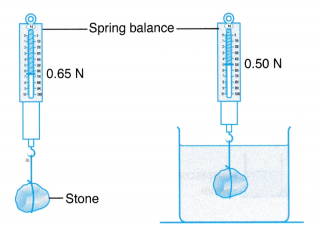Applying Archimedes' Principle 2What is the buoyant force acting on the stone when it is completely submerged in water?
Solution:
Buoyant force
= Actual weight – Apparent weight = 0.65 – 0.50 = 0.15 N

Example 5. Figure shows an empty oil drum floating on the surface of a pond.
Applying Archimedes' Principle 3
Draw and label the two forces acting on the oil drum.
Solution:
Applying Archimedes' Principle 4