Difference Between Speed And Velocity
- The ‘distance’ travelled by a body in unit time interval is called its speed. When the position of a body changes in particular direction, then speed is denoted by ‘velocity’. i.e. the rate of change of displacement of a body is called its Velocity.
- Speed is a scalar quantity while velocity is a vector quantity.
- \( \text{Speed}=\frac{\text{distance}}{\text{time}} \)
- \( \text{Velocity}=\frac{\text{displacement}}{\text{time}} \)
- Unit: In M.K.S. system = ms-1
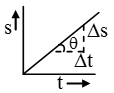
In C.G.S. system = cm/s - If time distance graph is given then speed can be given by the slope of the line, at given time
\( \text{V}=\frac{\text{ }\!\!\Delta\!\!\text{ s}}{\text{ }\!\!\Delta\!\!\text{ t}}=\text{Slope} \)
- The area of velocity time graph gives displacement travelled.
Types of speed
(a) Average and Instantaneous speed
Average speed: It is obtained by dividing the total distance travelled by the total time interval. i.e.
\( \text{Average speed}=\frac{\text{total}\,\,\text{distance}}{\text{total}\,\,\text{time}} \)
\( \text{Average}\,\text{velocity}=\frac{\text{displacement}}{\text{total}\,\,\text{time}} \)
- Average speed is a scalar, while average velocity is a vector.
- For a moving body average speed can never be –ve or zero (unless t → ∞), while average velocity can be i.e
\( {{v}_{av~}}>0\text{ while }\overset{\to }{\mathop{{{v}_{av}}}}\,>=or<\text{ }0 \) - In general average speed is not equal to magnitude of average velocity. However it can be so if the motion is along a straight line without change in direction
- If a particle travels distances L1, L2, L3 at speeds v1, v2, v3 etc respectively, then
\( {{v}_{av~}}=\frac{\Delta s}{\Delta t}=\frac{{{L}_{1}}+{{L}_{2}}+…..+{{L}_{n}}}{\frac{{{L}_{1}}}{{{v}_{1}}}+\frac{{{L}_{2}}}{{{v}_{2}}}+….+\frac{{{L}_{n}}}{{{v}_{n}}}}=\frac{\sum{Li}}{\sum{\frac{{{L}_{i}}}{{{v}_{i}}}}} \) - If a particle travels at speeds v1, v2 etc for intervals t1, t2 etc respectively, then
\( {{v}_{av~}}=\frac{{{v}_{1}}{{t}_{1}}+{{v}_{2}}{{t}_{2}}+….}{{{t}_{1}}+{{t}_{2}}+….}=\frac{\sum{{{v}_{1}}{{t}_{1}}}}{\sum{{{t}_{1}}}} \)
Instantaneous speed: The speed of a body at a particular instant of time is called its instantaneous speed.
\( =\underset{\Delta t\to 0}{\mathop{\lim }}\,\,\frac{\Delta s}{\Delta t}=\frac{ds}{dt} \)
(b) Uniform and Non uniform speed
Uniform speed: If an object covers equal distance in equal interval of time, then time speed graph of an object is a straight line parallel to time axis then body is moving with a uniform speed.
Non-uniform speed: If the speed of a body is changing with respect to time it is moving with a non-uniform speed.
Speed And Velocity Example Problems With Solutions
Example 1. The distance between two points A and B is 100 m. A person moves from A to B with a speed of 20 m/s and from B to A with a speed of 25 m/s. Calculate average speed and average velocity.
Solution: (i) Distance from A to B = 100 m
Distance from B to A = 100 m
Thus, total distance = 200 m
Time taken to move from A to B, is given by
\( {{t}_{1}}=\frac{\text{distance}}{\text{velocity}}=\frac{100}{20}=5\text{ seconds} \)
Time taken from B to A, is given by
\( {{t}_{2}}=\frac{\text{distance}}{\text{velocity}}=\frac{100}{25}=4\text{ seconds} \)
Total time taken = t1 + t2 = 5 + 4 = 9 sec.
∴ Average speed of the person
\( =\frac{\text{Total}\,\text{dis}\,\text{tan}\,\text{cecovered}}{\text{Total}\,\text{time}\,\text{taken}}=\frac{200}{9}=22.2\text{ m/s} \)
(ii) Since person comes back to initial position A, displacement will be zero, resulting zero average velocity.
Example 2. A car moves with a speed of 40 km/hr for first hour, then with a speed of 60 km/hr for next \(1\frac{1}{2}\) half hour and finally with a speed of 30 km/hr for next hours. Calculate the average speed of the car.
Solution: Distance travelled in first hour, is given by
s1 = speed × time = 40 km/hr × 1 hr = 40 km
Distance travelled in next half an hour, is given by
s2 = speed × time = 60 km/hr × \(\frac { 1 }{ 2 }\) hr = 30 km
Distance travelled in last \(1\frac{1}{2}\) hours, is given by
s3 = speed × time = 30 km/hr × \(\frac { 3 }{ 2 }\) hr = 45 km
Thus, total distance travelled = s1 + s2 + s3
= 40 + 30 + 45 = 115 km
Total time taken = 1 + \(\frac { 1 }{ 2 }\) + \(1\frac{1}{2}\) = 3 hours
Average speed = \(\frac { Total distance covered }{ Total time taken } \) = \(\frac { 115km }{ 3hrs }\)
= 38.33 km/hr
Example 3. Figure shows time distance graph of an object. Calculate the following :
(i) Which part of the graph shows that the body is at rest ?
(ii) Average speed in first 10 s.
(iii) Speeds in different parts of motion.
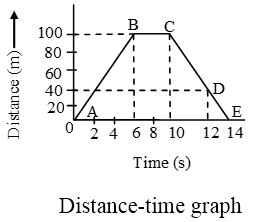
Solution: (i) The part BC shows that the body is at rest.
(ii) In first 10 seconds, distance travelled = 100m
\( \text{Average speed}=\frac{\text{total}\,\,\text{distance}}{\text{total}\,\,\text{time}} \)
\( =\frac{100}{10}=10\text{ m/s} \)
(iii) Speed of the object in part AB is given by slope = 100/6 = \(\frac { 50 }{ 3 }\) m/s
Speed of object in part BC = 0 m/s
Speed of the object in part CD
\( =\frac{100-40}{12-10}=\frac{60}{2}=30~\text{m/s} \)
Speed of object in part DE
\( =\frac{40-0}{14-12}=\frac{40}{2}=30~\text{m/s} \)
Example 4. Time-velocity graph of a particle is shown in Figure. Calculate the distance travelled in first seconds.
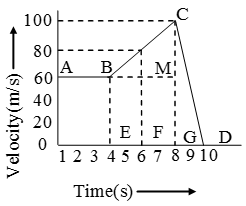
Solution: Distance travelled in first 8s is given by area OABCG
= area of rectangle OAMG + area of triangle BMC
= 8 × 60 + \(\frac { 1 }{ 2 }\) × 4 × 40
= 480 + 80 = 560 m.
Example 5. A cow walked along a curved path from P to Q, which is 70 m away from P. Q lies to the south-west of P. The distance travelled by the cow is 240 m and the time taken is 160 s.
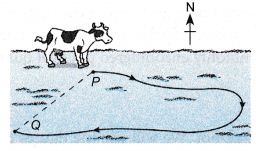
Calculate the
(a) average speed,
(b) average velocity,
of the cow moving from P to Q.
Solution:
Total distance travelled = 240 m
Displacement = 70 m
Time taken = 160 s

