What is the Hooke’s Law?
Hooke’s law states that the extension of a spring is directly proportional to the applied force provided the elastic limit is not exceeded.
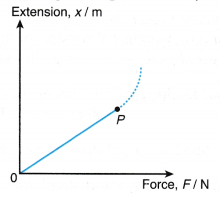
- Figure shows a graph of extension, x of a spring against applied force, F.
(a) The portion of graph from zero to P is where Hooke’s law applies.
(b) Beyond point P, Hooke’s law does not apply anymore.
(c) Point P is known as the elastic limit of the spring. Any force beyond point P will cause the spring to be permanently deformed.
- Figure shows a graph of extension, x of a spring against applied force, F.
- Sometimes, it is more convenient to plot the graph of F against x to formulate the formula for a spring that obeys Hookes law.
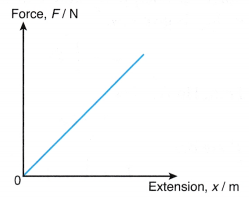
(a) Figure shows a graph of F against x for a spring. From the graph, F is directly proportional to x.
F ∝ x
Where, F = force on the spring,
x = extension of the spring. Therefore,
F = kx
where k is the gradient of the F-x graph.
(b) The value of k is known as the force constant of the spring. It is also known as the spring constant. Therefore,

The SI unit for k is N m-1.
(The unit N cm-1 is more commonly used)
Example 1. The graph in Figure shows the extension, x of a spring due to an applied force, F.
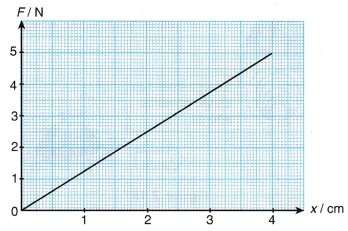
What is the force constant of the spring?
Solution:
The force constant of the spring is the gradient, k of the F-x graph. Therefore,
k = 5/4
= 1.25 cm N cm-1
Example 2. A spring with a force constant of 3.5 N cm-1 is extended 2.4 cm. Calculate the force applied for this extension.
Solution:
k = 3.5 N cm-1; x = 2.4 cm
F = kx
= 3.5 x 2.4
= 8.4 N