What is Law of Conservation of Momentum

Law of Conservation of Momentum

• According to law of conservation of momentum “if there is no force acting on a system, the momentum of the system remains unchanged.”
• Generalizing the situation ” if a group of bodies are exerting force on each other, their total momentum remains conserved before and after the interaction provided there is no external force acting on them.”
  i.e. m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂

Definition of Principle of Conservation of Momentum
The principle of conservation of momentum can also be defined as follows:

• The total momentum in a closed system is constant.
• A system consists of several objects acting on each other.
• A closed system is a system where the sum of its external forces (also known as resultant force) is zero.
• When the momentum is constant, we say the momentum is conserved.

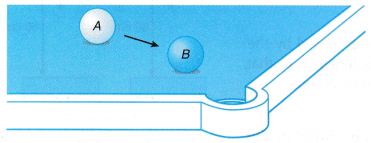
1. Figure shows two billiard balls, A and B. When ball A collides with ball B, ball A loses momentum and ball B gains the amount of momentum lost by ball A.
   
2. Figure (a) shows a boy standing on a skating board with a bowling ball in his hands.
   
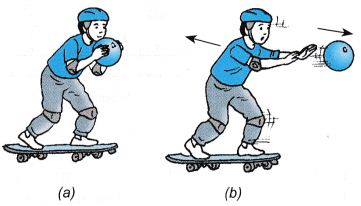
3. When he throws the ball forward, he moves backward. Initially, the respective momentums of both the boy and the ball is zero because both are at rest.
4. When the ball is thrown, the ball gains momentum. The boy gains an equal amount of momentum but in the opposite direction.
5. The above observations can be explained using the principle of conservation of momentum.
6. According to the principle of conservation of momentum, when two or more bodies act on each other, their total momentum remains constant, provided that there is no external force acting on them.

Experiment 1

Aim: To show that the total momentum of a closed system is conserved.
Problem: Is the total momentum in a closed system constant?
Hypothesis: The total momentum of a system after a collision/explosion is the same as the total momentum before the collision/explosion.
A. Collision
Materials: Cellophane tape, ticker tape, plasticine, two pins, two pieces of cork
Apparatus: Trolleys, plane, retort stands with clamps, power supply
Variables:
(a) Manipulated variable: Mass of trolley
(b) Responding variable: Velocity of trolley
Method:

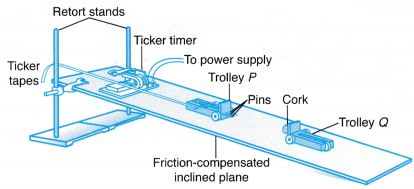
1. The apparatus is set up by attaching two pins in front of trolley P and two pieces of cork at the end of trolley Q as shown in Figure.
2. Trolley P is placed at the higher end of the plane and trolley Q is placed halfway down the plane and is at rest. A ticker tape is passed through the ticker timer and is attached to trolley P.
3. After the ticker timer is switched on, trolley P is given a push towards trolley Q. Both trolleys will stick together and move down the plane after the collision.
4. The tapes are analysed to determine the following:
   (a) velocity of trolley P before the collision, u_p.
   (b) velocity of trolley P and trolley Q after the collision, v.
5. Using identical trolleys, the mass of each trolley can be taken as 1 unit of mass. The experiment is repeated as follows:
   (a) two stacked trolleys collide with one trolley at rest,
   (b) three stacked trolleys collide with one trolley at rest.

Results:

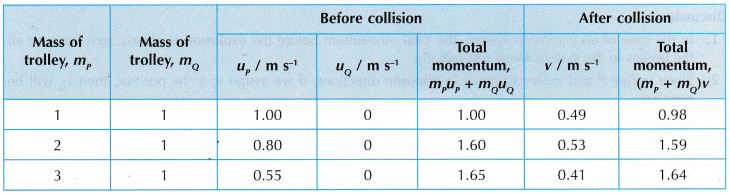
Discussion:
Before collision, velocity of trolley Q, u_Q = 0 because it is at rest.
Conclusion:
It is found that the total momentum after the collision is the same as that before the collision. The hypothesis is accepted.

B. Explosion
Materials: Cellophane tape, ticker tape, mallet
Apparatus: Trolleys, power supply
Variables:
(a) Manipulated variable: Mass of trolley
(b) Responding variable: Velocity of trolley
Method:

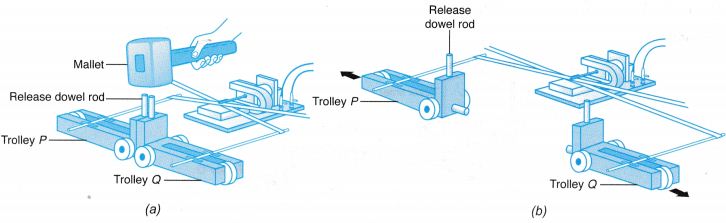
1. Trolley P and trolley Q are set up facing each other on a smooth table as shown in Figure (a). The spring-loaded plunger of trolley P is compressed.
2. Two ticker tapes are passed through the ticker timer, one attached to trolley P and another to trolley Q.
3. After the ticker timer is switched on, the plunger of trolley P is released by tapping the release dowel rod with a mallet. The trolleys will ‘explode’ and move apart in opposite directions as shown in Figure (b).
4. From the tapes obtained, the velocities of trolley P, vp and trolley Q, v_Q are determined.
5. The experiment is repeated by using two and then three stacked trolleys placed facing trolley Q.

Results:

Discussion:

1. In the case of an explosion system, the total momentum before the explosion is always zero because all the bodies in the system are at rest initially.
2. Since trolley P and trolley Q move in opposite directions, if we assign v_P to be positive, then v_Q will be negative.

Conclusion:
It is found that the total momentum before and after the explosion are the same and both are equal to zero. The hypothesis is accepted.

Applications of Conservation of Momentum

1. (a) Figure shows the launching of a rocket. A rocket carries liquid hydrogen fuel and liquid oxygen. When a mixture of hydrogen and oxygen burns in the combustion chamber during launching, jets of hot gas are expelled at very high speed through the exhausts. This produces a very large momentum.

   

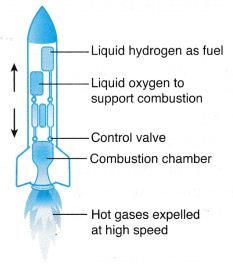
   (b) According to the principle of conservation of momentum, an equal and opposite momentum is produced causing the rocket to propel upwards.

2. (a) Figure shows a jet engine. Air in front of the engine is sucked into the combustion chamber by the rotating compressor blades. In the combustion chamber, fuel is injected and burnt with the compressed air.

   

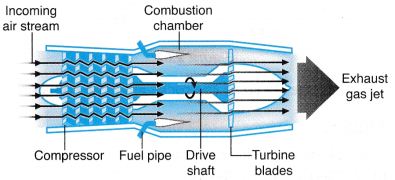
   (b) The exploding hot jet of gases is expelled from the combustion chamber. This produces a very large momentum.
   (c) According to the principle of conservation of momentum, the expulsion of the hot gases produces an equal and opposite momentum, causing the jet plane to move forward.

3. (a) When a bullet is fired from a submachine gun, the exploding gases from the bullet cause it to be shot out at a very high speed, producing a very big momentum.

   

   (b) An equal and opposite momentum is produced and this causes the submachine gun to recoil.

Law of Conservation of Momentum Example Problems with Solutions

Example 1. A rifle of mass 5 kg fires a bullet of mass 40 gm. The bullet leaves the barrel of the rifle with a velocity 200 m/s. If the bullet takes 0.004 s to move through the barrel, calculate the following:
(i) recoil velocity of the rifle and
(ii) the force experienced by the rifle due to its recoil.
Solution:    (i) Given mass of the rifle, m₁ = 5 kg
Mass of the bullet, m₂ = 40 gm = 0.04 kg
Initial velocities, u₁ = 0, u₂ = 0
After firing velocity of the bullet, v₂ = 200 m/s
Velocity of the rifle, v₁ = ?
Applying the law of conservation of momentum, we get
m₁u₁ + m₂u₂ = m₁v₁ + m₂v₂
0 + 0 = 5 × v₁ + 0.04 × 200
\({{v}_{1~}}=\frac{0.04\times 200}{5}=-1.6\text{ m/s}\)
(ii) Initial momentum of the rifle = 0
Final momentum of the rifle = 5 kg ×(–1.6)
= – 8 kg-m/s
Time interval = 0.004 s
\( \therefore \text{Force}=\frac{\text{Change}\,\text{in}\,\text{momentum}}{\text{Time}\,\text{interval}} \)
\( =\frac{-8kg-m{{s}^{-1}}}{0.004}=-2000\text{ N} \)

Example 2. A bullet of mass 20 gm moving with a velocity 200 m/s gets embedded into a wooden block of mass 980 gm suspended by a string. Calculate velocity acquired by the combined system.
Solution:    Mass of the bullet, m₁ = 20 gm = 0.02 kg
Velocity of the bullet, u₁ = 200 m/s
Momentum of the bullet = m₁u₁
= 0.02 × 200 kg-m/s = 4 kg-m/s
Now, the bullet gets embedded into a wooden block of mass 980 gm. The mass of the block and bullet = 980 + 20
= 1000 gm = 1kg
Let the velocity of the combined system = v
∴ Momentum of the combined system
= 1 × v kg-m/s = v kg-m/s
Now, applying the law of conservation of momentum,
m₁u₁ = (m₁ + m₂)v
or   4 = v
∴ v = 4 m/s = 4 kg m/s

Example 3. A rifle man, who together with his rifle has a mass of 100 kg, stands on a smooth surface fires 10 shots horizontally. Each bullet has a mass 10 gm a muzzle velocity of 800 m/s. What velocity does rifle man acquire at the end of 10 shots?
Solution:    Let m₁ and m₂ be the masses of bullet and the rifleman and v₁ and v₂ their respective velocities after the first shot. Initially the rifleman and bullet are at rest, therefore initial momentum of system = 0.
As external force is zero, momentum of system is constant
i.e. initial momentum = final momentum
= m₁v₁ + m₂v₂
\(\Rightarrow {{v}_{2}}=\frac{{{m}_{1}}{{v}_{1}}}{{{m}_{2}}}=-\frac{(10\,\times \,{{10}^{-3}}kg)(800\,m/s)}{100kg}\)
= – 0.08 m/s
Velocity acquired after 10 shots
= 10 v₂ = 10 x (–0.08)
= – 0.8 m/s.
i.e, the velocity of rifle man is 0.8 m/s in a direction opposite to that of bullet.

Example 4. A body of mass 1 kg strikes elastically with another body at rest and continues to move in the same direction with one fourth of the initial velocity. What will be the mass of the other body ?
Solution:    Given that,
Initial velocity = u
Final velocity = \(\frac { u }{ 4 }\)
So by conservation of momentum, we have
1 × u + 0 = 1 × \(\frac { u }{ 4 }\) + m × v₂
⇒ mv₂ = \(\frac { 3u }{ 4 }\)           …(1)
and by conservation of energy, we have
\( \Rightarrow \frac{1}{2}\times 1\times {{u}^{2}}+0=~~\frac{1}{2}\times 1~{{\left( \frac{u}{4} \right)}^{2}}+~m{{v}_{2}}^{2}\)
\(\Rightarrow \text{m}{{\text{v}}_{\text{2}}}^{\text{2}}=\frac{15}{16}{{u}^{2}}\text{       }……\text{ (2)}\)
from equation (1) and (2),
\(=\frac{{{(m{{v}_{2}})}^{2}}}{mv_{2}^{2}}=\frac{(9/16){{u}^{2}}}{(15/16){{u}^{2}}}\)
or m = 0.6 kg

Example 5. Figure shows two rocks moving towards each other along a straight line. After colliding with each other, the two rocks lump together.
Calculate the speed of the rocks after the collision.

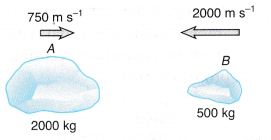
Solution:

Example 6. An astronaut with mass of 80 kg throws a 40 kg tool box in order to be able to get back to the space capsule.
If the box is thrown at a velocity of 6 m s^-1, what is the velocity of the astronaut after throwing the tool box?

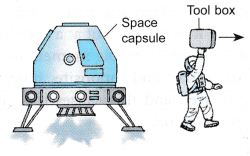
Solution:

Example 7. Figure shows two identical boxcars of a train being coupled at a railway station. Each boxcar has a mass of 2.5 × 10⁴ kg. The velocities of boxcar 1 and boxcar 2 before the coupling are 1.0 m s^-1 and 0.8 m s^-1 respectively.
Find the velocity, v, of the boxcars after they are coupled. State one assumption in your calculation.

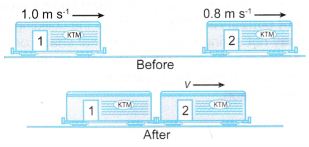
Solution: