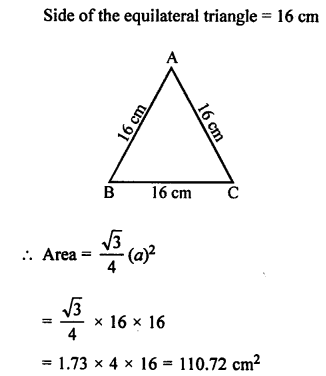
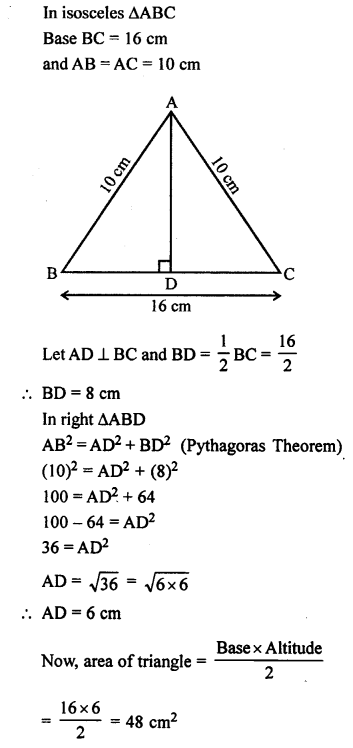
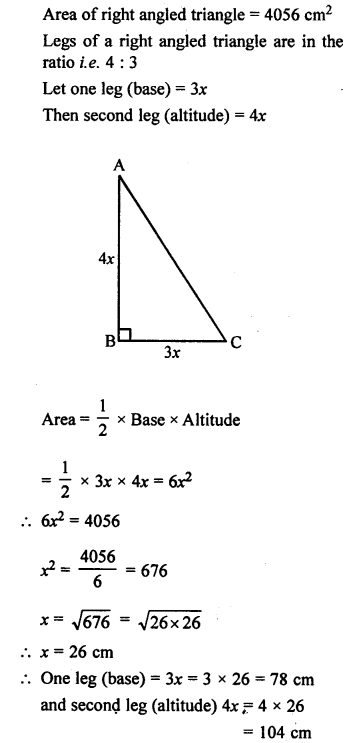
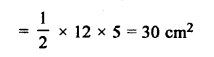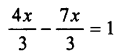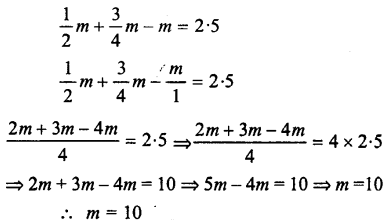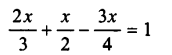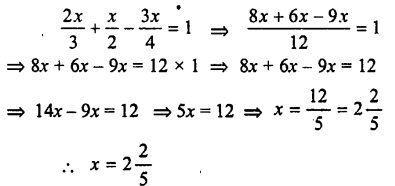Selina Concise Chemistry Class 7 ICSE Solutions – Metals and Non-metals
ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 7 Chemistry. You can download the Selina Concise Chemistry ICSE Solutions for Class 7 with Free PDF download option. Selina Publishers Concise Chemistry for Class 7 ICSE Solutions all questions are solved and explained by expert teachers as per ICSE board guidelines.
Selina Class 7 Chemistry ICSE SolutionsPhysicsBiologyMathsGeographyHistory & Civics
Selina Concise ICSE Solutions for Class 7 Chemistry Chapter 6 Metals and Non-metals
Points to Remember :
- Knowledge of chemistry plays a vital role in the development of human society and civilization.
- Metals are known to man from ancient times. Metals are used to make our life comfortable.
- Non-metals form another class of elements, e.g. hydrogen, oxygen, carbon, etc. They are used for various purposes.
- Alloys are homogeneous solid mixtures containing two or more metals e.g. steel, brass, bronze.
- Common salt, hydrocloric acid, carbohydrates, fats, proteins, vitamins, occur naturally and can also be prepared artificially.
- Fertilizers are artificially prepared substances, which are necessary for the proper growth of crops.
- There are a number of man-made materials that are used in our daily life for various purposes, e.g., cement, plaster of pairs, plastics.
- Medicines are used to cure diseases.
- Solution is a homogenous mixture of solute and solvent.
- Soda water is prepared by dissolving carbon dioxide in water under high pressure.
- Syrup is a highly concentrated sugar solutions. It contains a specific flaviour.
EXERCISE
1. Name a metal
- that is most malleable : Pure gold
- that is brittle : Zinc
- as precious as gold : Platinum
- that can be cut with knife : Sodium
- used in making electric cables : Copper
- used as a thermometric liquid : Mercury
- that is the best conductor of electricity : Silver
2. Name a non-metal that is :
- a good conductor of heat and electricity : Graphite (Carbon)
- hardest naturally occurring substance : Diamond (Carbon)
- used to kill germs in water : Chlorine
- lustrous : Iodine
- used for filling into electric bulbs : Argon
- used for cancer therapy : Radon
- liquid at room temperature : Bromine
3. Mention two uses of the following metals and non-metals
(a) Iron :
It is used to make pipes, tanks, railing, etc.
It is used in the construction of power transmission towers.
(b) Aluminium :
It is used to make electric wires.
It is used to make utensils, cans, window fram’es, etc.
(c) Gold :
It is used for making ornaments and coins.
It is used in the manufacture of electronic devices like computers, telephones, home appliances, etc.
(d) Oxygen :
It is used by all living beings for breathing.
It is important for combustion.
(e) Iodine :
It is used in photographic films in the form of potassium iodide.
It is added to salt to make it iodized salt which is necessary for the growth of human body.
4. Give reasons :
(a) Magnesium is used in fire works.
Ans : Magnesium is used in fire works because it bums with a dazzling light.
(b) Aluminium is used in making aircrafts.
Ans : Aluminium is used in making aircrafts because it is light and strong. It is mixed with other metals to make it stronger.
(c) Copper is used in making electric cables.
Ans : Copper is ductile and a very good conductor of heat and electricity. This is the reason that copper is used in making electric cables.
(d) Graphite is used in the leads of pencils
Ans : Graphite turns paper black that is why it is used in the leads of pencils.
(e) Impure diamond is used to cut glass
Ans : Impure diamond is used to cut glass becuase it is the hardest substance and can easily exert force required for cutting.
(f) Gold is mixed with copper and nickel.
Ans : Pure gold is a very soft metal. It cannot be moulded into ornaments so it is mixed with copper and nickel so that it becomes harder and bit cheaper also.
(g) Tungsten is used in electric bulbs.
Ans : It is a shiny grey metal, in solid state at room temperature. It can withstand high temperature because it has highest melting point among metals. Hence, it is used in electric bulbs.
5. Name the metals present in the following alloys
- Brass— Copper and zinc
- Bronze— Copper and tin
- Duralumin— Aluminium and copper
- Stainless steel— Iron, chromium, nickel
6. Give four differences between metals and non-metals with reference to their
(a) Melting point and boiling point,
(b) Conductivity of heat and electricity,
(c) Malleability
(d) Solubility
| Metals | Non-metals | |
| Melting point and boiling point | Metals have both high high melting point and boiling point. | Non-metals have both low melting and low boiling point. |
| Conductivity of heat and electricity | They are good conductors of heat and electricity. | Nofi-metals are bad conductors of heat and electricity. |
Malleabi lity | Metals are ususally malleable. | All non-metal are non- malleable. |
Solubility | Metals are generally insoluble in water and other organic solvents. | They are both soluble and insoluble |
7. What are metalloids?
Ans : Metalloids are the elements which show some properties of metals and some properties of non-metals. They all are solids. They are silicon, boron, arsenic, antimony, germanium, tellurium and polonium.
8. Give two uses of
(a) Silicon :
- Highly pure silicon is used in making microchips for computers, transistors, solar cells, rectifiers and other solid state devices that are used extensively in the electronic and present space age industries.
- It is used in the manufacture of a waterproof material called “silicone”. Silicone is used to make bags, umbrellas, raincoats, etc.
- It is an important substance present in steel, an alloy of carbon.
(b) Antimony :
- Antimony is used in electric industry to make semiconductor devices.
- It is alloyed with lead to improve its hardness and strength and is used in batteries.
- It is also used in printing presses as type metal.
(c) Tungsten :
- It is used in making electrodes.
- It is used in heating elements.
- It is used as filaments in electric bulbs and cathode ray tubes.
(d) Germanium:
- Germanium is used as a semiconductor.
- It is used as a transistor in many electronic applications when mixed with arsenic, gallium, antiomony, etc.
- Germanium is also used to form alloys and as a phosphor in fluorescent lamps
OBJECTIVE TYPE QUESTIONS
1. Fill in the blanks :
(a) The most ductile metal is silver.
(b) A metal stored in kerosene oil is sodium.
(c) Tungsten metal is a poor conductor of heat.
(d) Pure gold is a soft metal.
(e) Silicon carbide is the hardest compound known to us.
(f) A non-metal used to purify water is phosphorus.
(g) A metal that gives dazzling effect to crackers when they explode is magnesium.
(h) A chemical compound that makes up the striking heads of match sticks is sulphur.
2. Match the following :

3. Write ‘true’ or ‘false’ for the following statements :
(a) Silver is used to make electric cables : False
(b) Iodine acts as an antiseptic in the form of tincture of iodine : True
(c) Sodium can be cut with a knife : True
(d) Antimony is a metal : False
(e) Sand is an oxide of silicon : True
MULTIPLE CHOICE QUESTIONS
1. The noble gas used in advertising signboards is
(a) Helium
(b) Neon
(c) Argon
(d) Krypton
2. A metal with melting point less than 50°C is
(a) Gallium
(b) Iron
(c) Gold
(d) Aluminium
3. A metal which is neither ductile nor malleable is
(a) Copper
(b) Silver
(c) Zinc
(d) Aluminium
4. Rust is a hydrated oxide of iron which is
(a) Reddish brown
(b) Green
(c) White
(d) Black
5. Aluminium is not used to make :
(a) Foils
(b) Wires
(c) Fireworks
(d) Utensils
6. A metalloid used in the manufacture of microchips used in computer is :
(a) Antimony
(b) Germanium
(c) Silicon
(d) Arsenic
7. A metalloid used to make glass :
(a) Sulphur
(b) Germanium
(c) Silicon
(d) Antimony