What is an Exponent?
Exponents
The repeated addition of numbers can be written in short form (product form).
 Examples:
Examples:

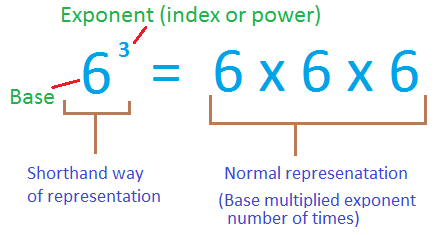
Also, we can write the repeated multiplication of numbers in a short form known as exponential form.
For example, when 5 is multiplied by itself for two times, we write the product 5 × 5 in exponential form as 52 which is read as 5 raised to the power two.
Similarly, if we multiply 5 by itself for 6 times, the product 5 × 5 × 5 × 5 × 5 × 5 is written in exponential form as 56 which is read as 5 raised to the power 6.
In 56, the number 5 is called the base of 56 and 6 is called the exponent of the base.
In general, we write,
An exponential number as ba, where b is the base and a is the exponent.
The notation of writing the multiplication of a number by itself several times is called the exponential notation or power notation.
Thus, in general we find that :
If ‘a’ is a rational number then ‘n’ times the product of ‘a’ by itself is given as a × a × a × a ….. , n times and is denoted by an, where ‘a’ is called the base and n is called the exponent of an.
Read More:
Examples
1. Write the following statements as repeated multiplication and complete the table:
| S.No. | Statements | Repeated Multiplication | Short form |
| (i) | 3 multiplied by 3 for 6 times | 3 × 3 × 3 × 3 × 3 × 3 = 729 | 36 |
| (ii) | 2 multiplied by 2 for 3 times | 2 × 2 × 2 | 23 |
| (iii) | 1 multiplied by 1 for 7 times | 1 × 1 × 1 × 1 × 1 × 1 × 1 | 17 |
2. Write the base and exponent of following numbers. And also write in expanded form:
| S.No. | Numbers | Base | Exponent | Expanded Form | Value |
| (i) | 34 | 3 | 4 | 3 × 3 × 3 × 3 | 81 |
| (ii) | 25 | 2 | 5 | 2 × 2 × 2 × 2 × 2 | 32 |
| (iii) | 33 | 3 | 3 | 3 × 3 × 3 | 27 |
| (iv) | 22 | 2 | 2 | 2 × 2 | 4 |
| (v) | 17 | 1 | 7 | 1 × 1 × 1 × 1 × 1 × 1 × 1 | 1 |
Exponents of Negative Integers
When the exponent of a negative integer is odd, the resultant is a negative number, and when the power of a negative number is even, the resultant is a positive number.When the exponent of a negative integer is odd, the resultant is a negative number, and when the power of a negative number is even, the resultant is a positive number.
or (a negative integer) an odd number = a negative integer.
(a negative integer) an even number = a positive integer.
Examples:
Ex.1 Express 144 in the powers of prime factors.
Solution:
144 = 16 × 9 = 2 × 2 × 2 × 2 × 3 × 3
Here 2 is multiplied four times and 3 is multiplied 2 times to get 144.
∴ 144 = 24 × 32
Ex.2 Which one is greater : 35 or 53 ?
Solution:
35 = 3 × 3 × 3 × 3 × 3 = 9 × 9 × 3
= 81 × 3 = 243
and 53 = 5 × 5 × 5 = 25 × 5 = 125
Clearly, 243 > 125
∴ 35 > 53