Concise Maths class 7 Answers

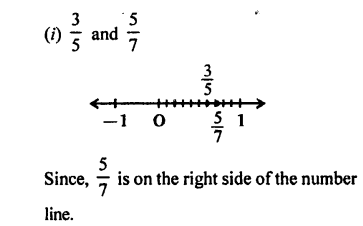
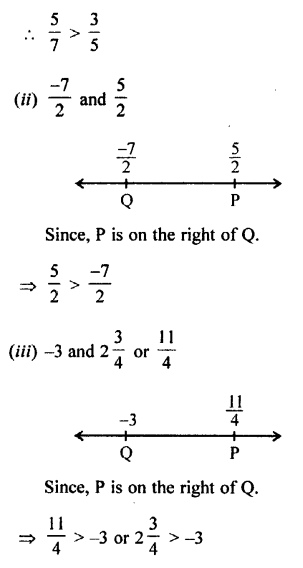
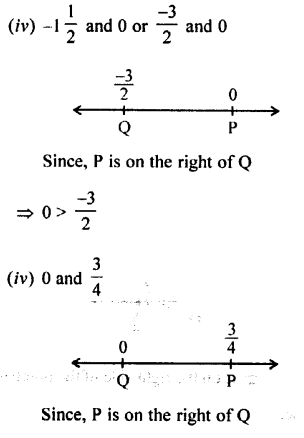
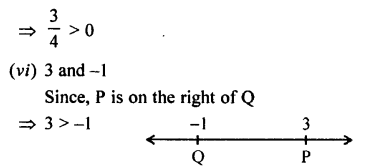
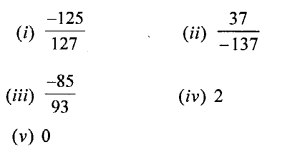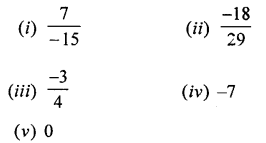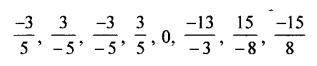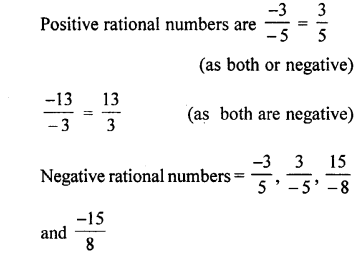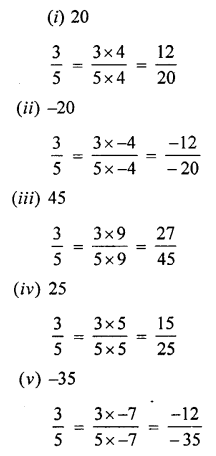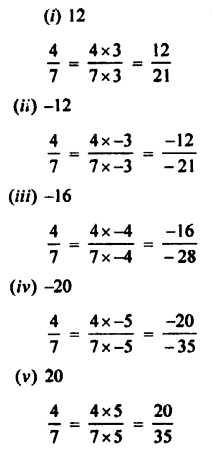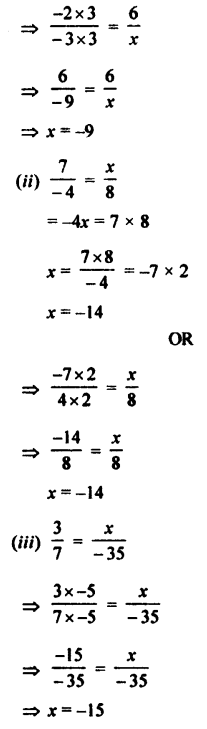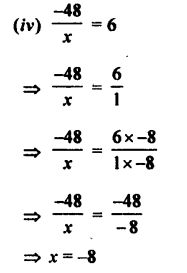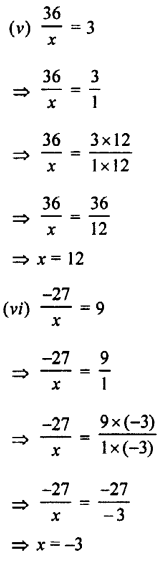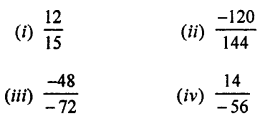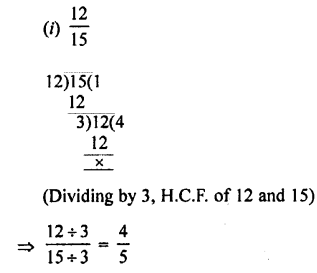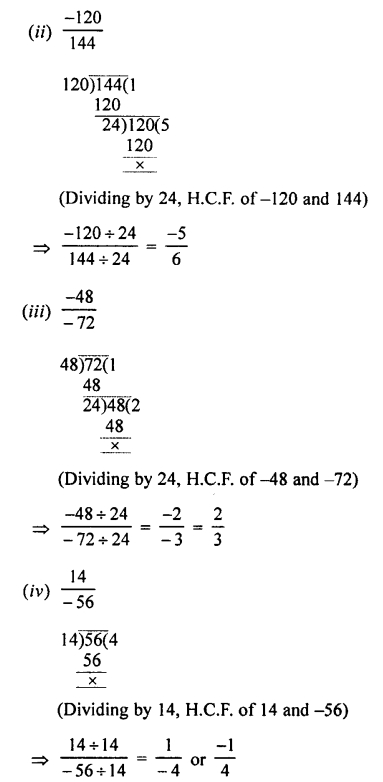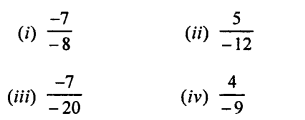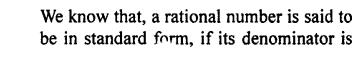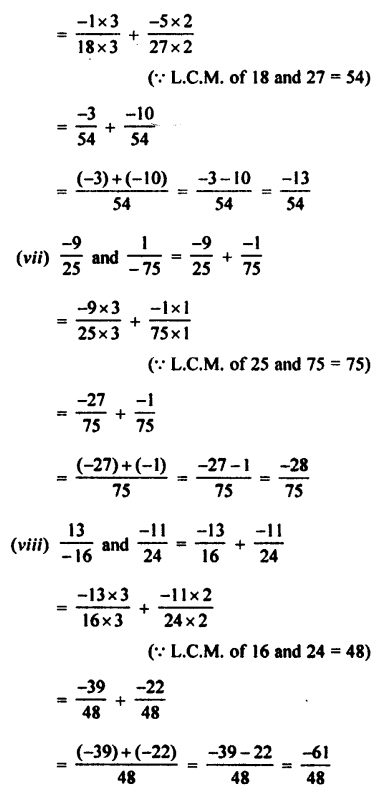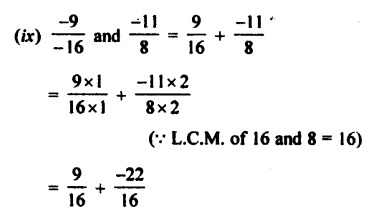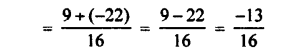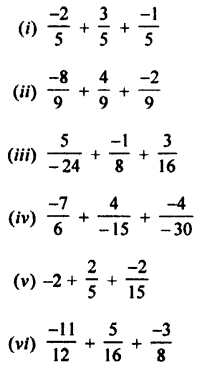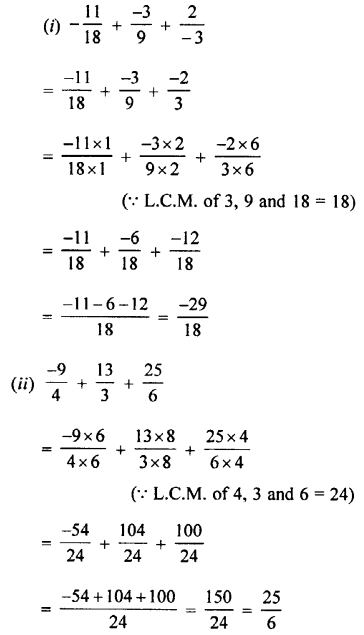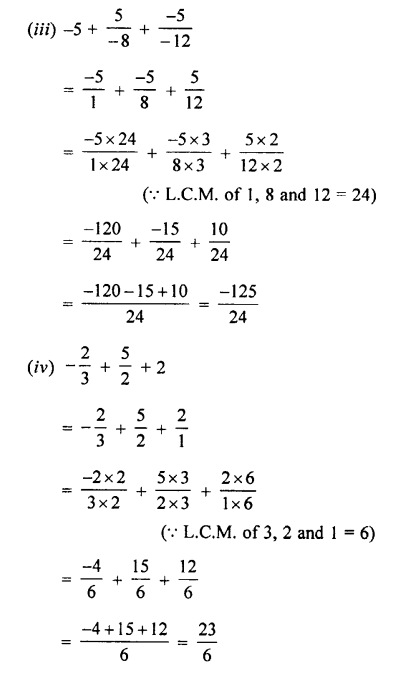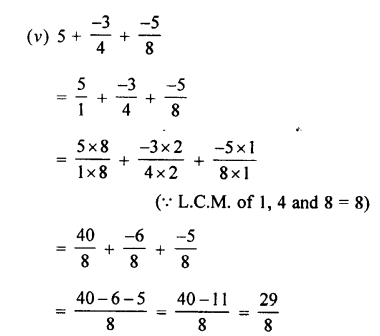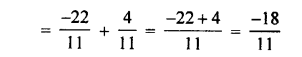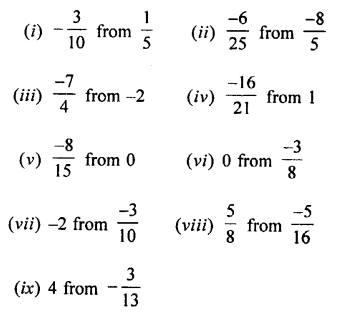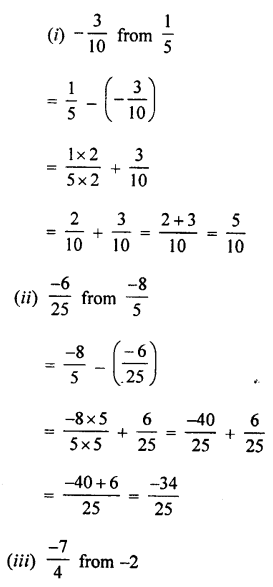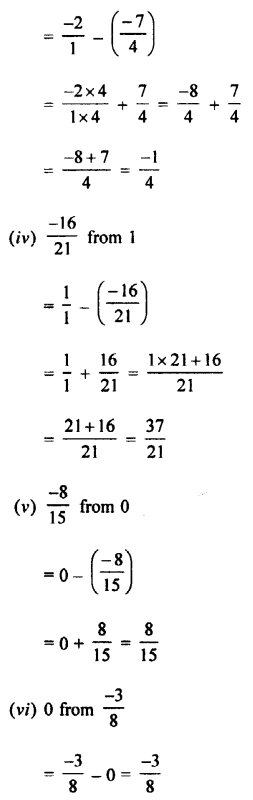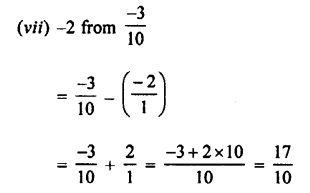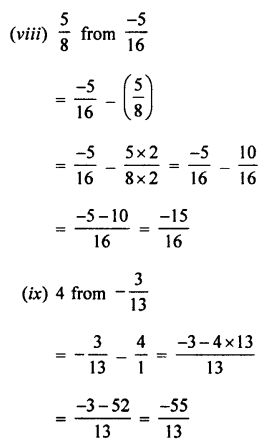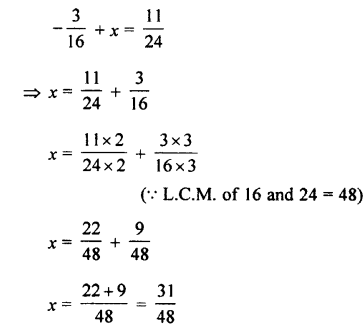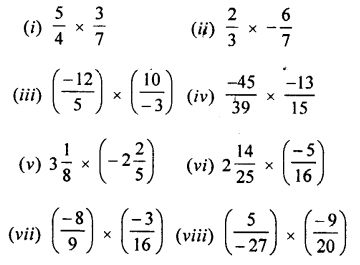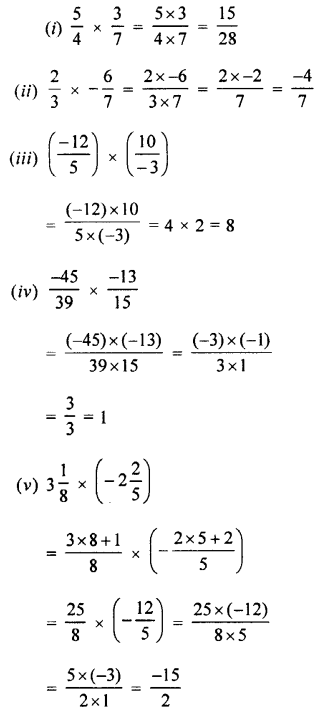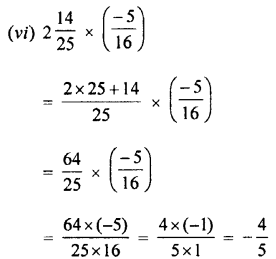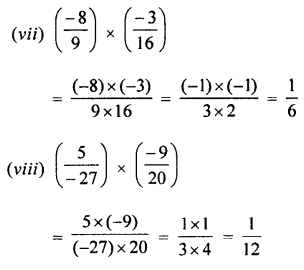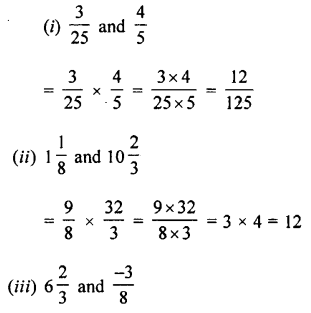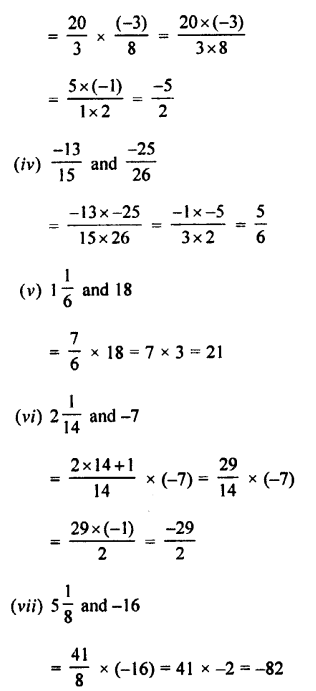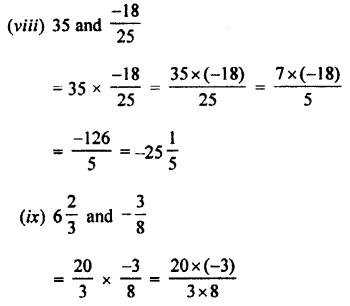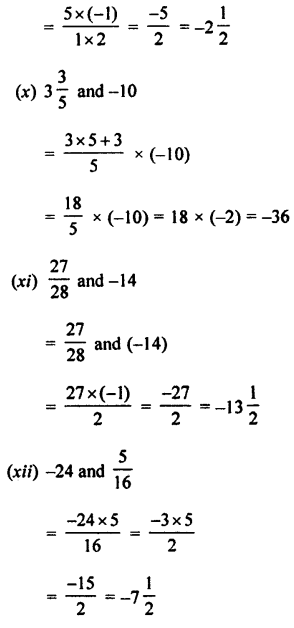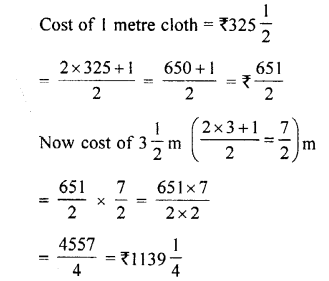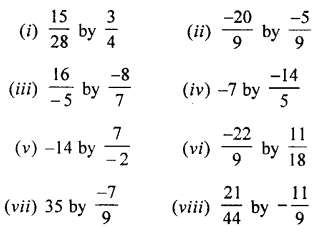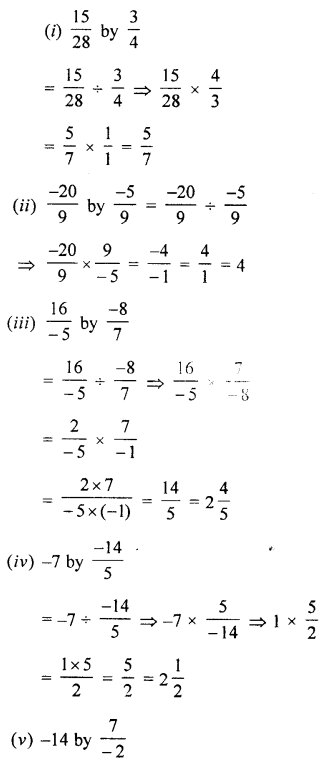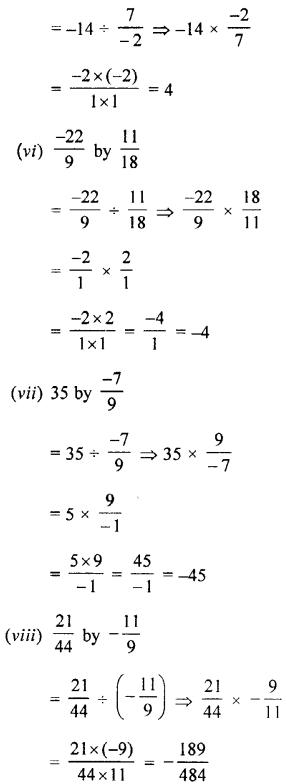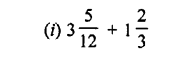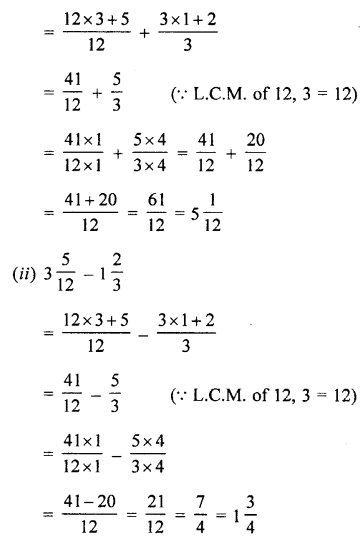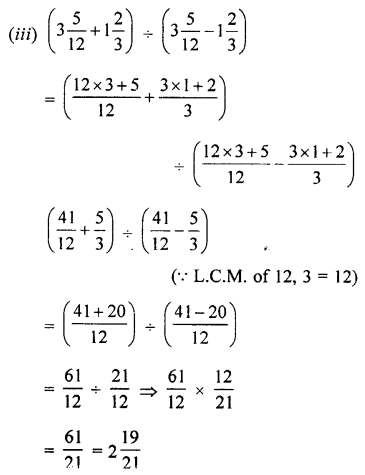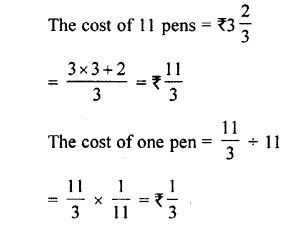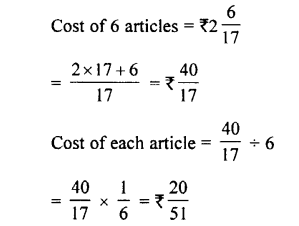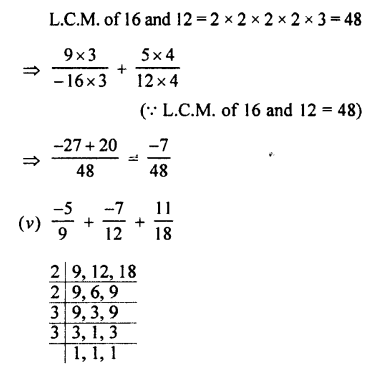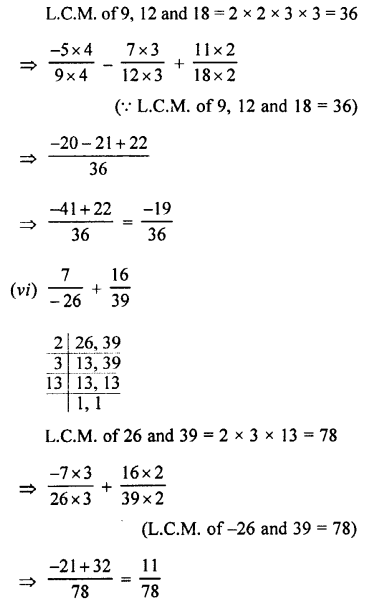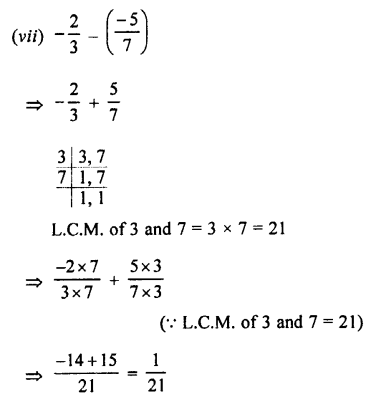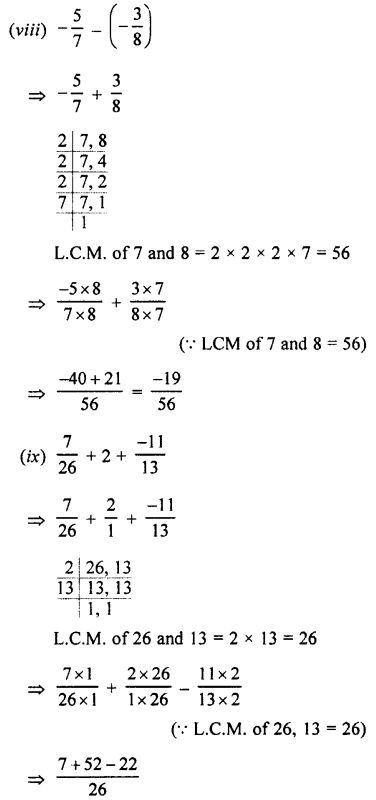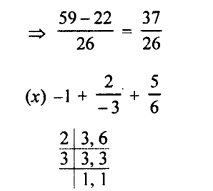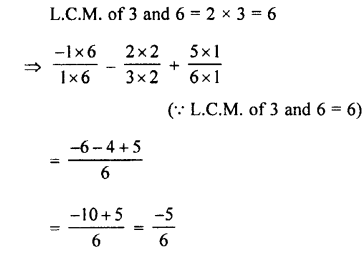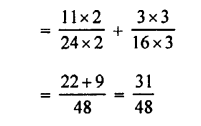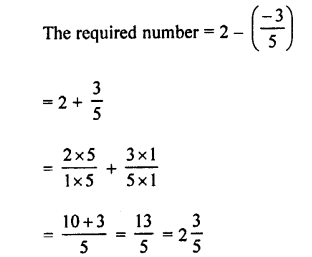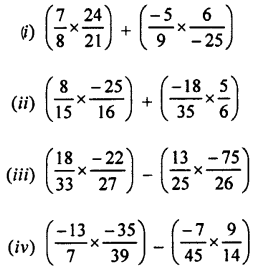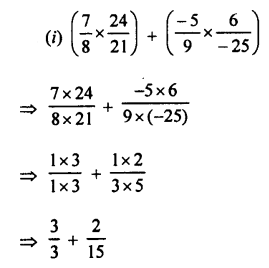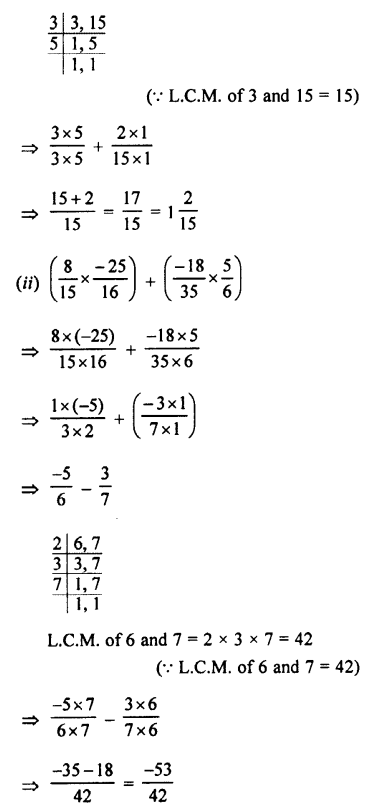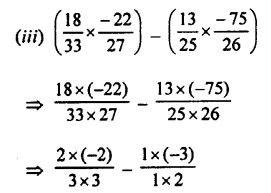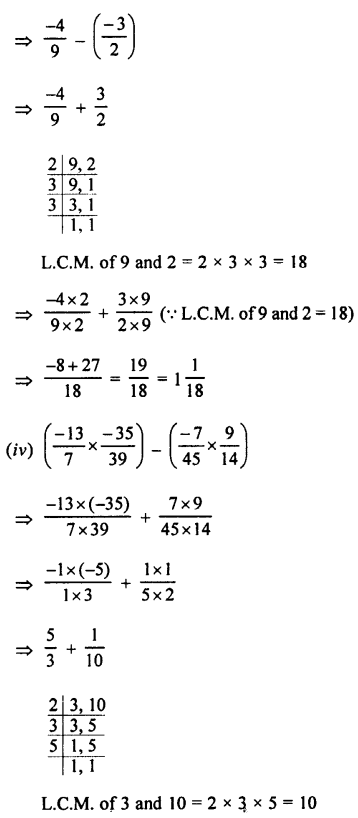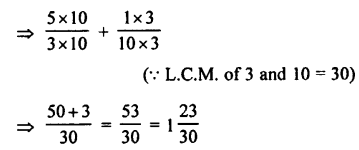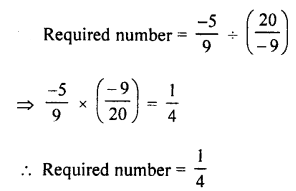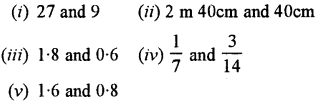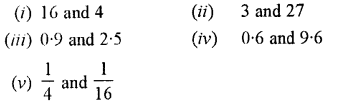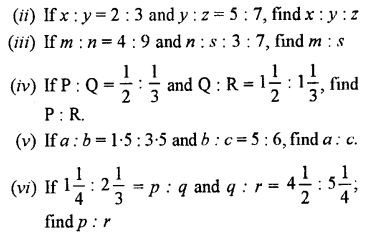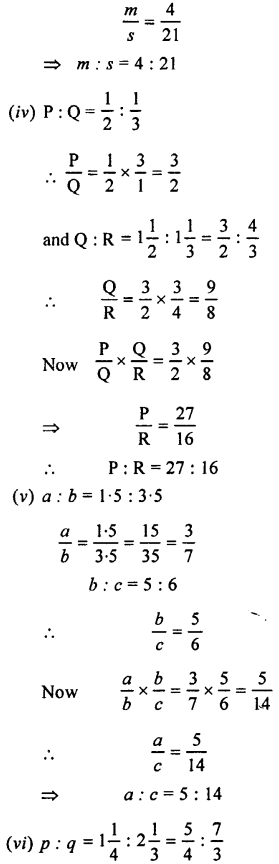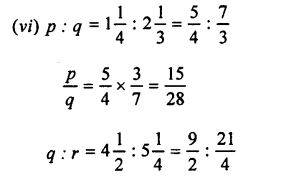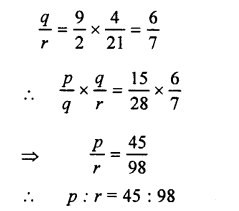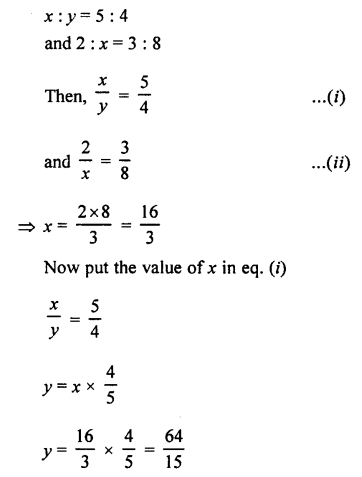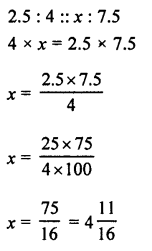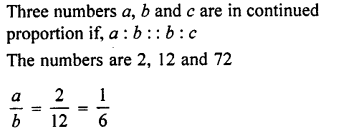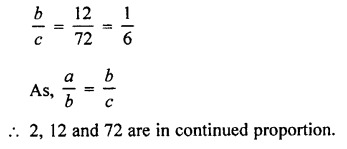Selina Concise Mathematics Class 7 ICSE Solutions Chapter 4 Decimal Fractions (Decimals)

Selina Publishers Concise Mathematics Class 7 ICSE Solutions Chapter 4 Decimal Fractions(Decimals)

ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions

APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 7 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 7 with Free PDF download option. Selina Publishers Concise Mathematics for Class 7 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.

Selina Class 7 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics

POINTS TO REMEMBER

1. Decimal fraction (or a decimal number)
   A decimal fraction is a fraction whose denominator is 10 or a higher power of 10.
   In order to express a given decimal fraction in shorter form, the denominator is not written but its absence is shown by a dot which is called a decimal point inserted in a proper place.
   Note :
   (i) When there is no number is the left of the decimal point, generally, a zero is written.
   (ii) Generally, a decimal fraction has two parts, the first part which is on the right ox the decimal point is called decimal part and the part on the left side of the decimal point, is called integeral part.
   (iii) The decimal part is always less than 1.
2. Reading Decimal Numbers
   The integral part is read according to its value and the decimal part is read by naming each digit, in order, separately
3. Converting a decimal number into a vulgar fraction :
   Remove the decimal point from the decimal number and write in its denominator with as many zeros as the number of digits are in the decimal parts to the right of 1.
   In the decimal number, the name of each place is given as under is the place value chart:

   Thousands	Hundreds	Tens	Units	•	Tenths	Hundredths	Thousandth
   				Decimal point			and so on

4. Converting a given fraction in to a decimal fraction :
   (a) When the denominator in given fraction is 10. 100, 1000 etc., then count from extreme right to left, mark decimal point after as many digits of the numerator as there are zeroes in the denominator.
   (b) When the denominator of the given number is other then 10 or higher power of 10, then divide in an ordinary way and mark the decimal point in the quotient just after the division of unit digit is completed. After this, any number of zeroes can be borrowed to.complete the division.
   Note : The number of figures that follow the decimal part is called the number of decimal places.
5. Addition and Subtraction of decimal numbers.
   (a) Addition : Write the given decimal numbers in such a way, that the decimal points of all the numbers fall in the same vertical line. Digits with the same place value are placed one below the other units are written below units, tens below tens and so on.
   Addition is started from the right side, as done in the usual addition (empty places may be filled up by zeroes). In the result (total), the decimal point is placed under decimal points of the numbers added.
   (b) Subtraction : In subtraction also, the numbers are written in such a way that their decimals are in ihe same vertical line. Digits with the same place value are placed one below the other (empty places may be filled by zeroes).
   Subtraction is started from the right side, as in the case of normal subtraction. In the result, decimal point is placed just under the other decimal points.
6. Multiplication of decimal numbers :
   (1) Multiplication by 10,100, 1000 etc. shift the decimal point, in the multiplicand, to the right by as many digits as there are zeroes in the multiplier.
   (2) Multiplication by a whole number : Multiply in an ordinary way, without considering the decimal point. In the product, the decimal point should be fixed by counting as many digits from the right as there are decimal places in the multiplicand.
   Thus, (i) 0.3 x 6 = 1.8 (ii) 0.26 x 18 = 4.68 and so on.
   (3) Multiplication of a decimal number by another decimal number :
   Multiply the two numbers in a normal way, ignoring their decimals. In the product, decimal point is fixed counting from right, the digits equal to the sum of decimal places in the multiplicand and the multiplier.
   Thus, 32.5 x ().()7 = 2.275
   Since, the multiplicand (32.5) has one decimal place and multiplier (0.07) has two decimal places, their product will have 1+2 = 3 decimal places.
7. Division of decimal numbers :
   (1) Division by 10, 100, 1000 etc : Shift the decimal points to the left as many digits as there are
   zeroes in the divisor. .
   (2) Division by a whole number : Divide in the normal manner, ignoring the decimal, and mark tire decimal point; in the quotient, while just crossing over the decimal point in the dividend.
8. Recurring Decimals :
   On performing a division, sometimes we find that the same remainder is left, no matter how long we continue the division process. For this reason, the same digit appeares again and again in the quotient. This fact is shown by puting a dot as a bar over the repeating digits.
9. Rounding off of decimal numbers :
   (i) If the answer required is correct to two decimal places, we retain digits upto three decimal places.
   (ii) If the digit in the third decimal place is five or more than five, then the digit in the second decimal place is increased by one and, if the digit in the third decimal place is less than five, then the digit in the second decimal place is not altered.
   (iii)The third digit which was retained is now omitted.
   Thus, for getting 8.4813 correct to two decimal places.
   Write the given number upto three decimal places i.e. 8.481.
   Since, the digit in the third decimal place is 1 which is less than 5.
   ∴The digit in the second decimal place is not altered.
   And, so 8.4813 = 8.48, correct to two decimal places.
   In the same way, to get 3.946824 correct to nearest thousandths i.e., correct to three decimal places, first write it as 3.9468.
   Then according to the rule, the digit in the third place changes from 6 to 7.
   3.9468 = 3.947, correct to three decimal places.

Decimal Fractions Exercise 4A – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Convert the following into fractions in their lowest terms :
(i) 3.75
(ii) 0.5
(iii) 2.04
(iv) 0.65
(v) 2.405
(vi) 0.085
(vii) 8.025

Answer:

Question 2.
Convert into decimal fractions

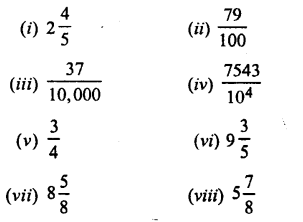
Answer:

Question 3.
Write the number of decimal places in :
(i) 0.4762
(ii) 7.00349
(iii) 8235.403
(iv) 35.4
(v) 2.608
(vi) 0.000879

Answer:
(i) In 0.4762, there are four places.
(ii) In 7.00349, there are five places.
(iii) In 8235.403, there are three places.
(iv) In 35.4, there is one place.
(v) In 2.608, there are three places.
(vi) In 0.000879, there are six places.

Question 4.
Write the following decimals as word statements :
(i) 0.4,0.9,0.1
(ii) 1.9, 4.4, 7.5
(iii) 0.02, 0.56, 13.06
(iv) 0.005,0.207, 111.519
(v) 0.8, 0.08, 0.008, 0.0008
(vi)256.1, 10.22, 0.634

Answer:
(i) 0.4 = zero point four, 0.9 = zero point nine, 0.1 = zero point one.
(ii) 1 .9 = one point nine, 4.4 = four point four, 7.5 = seven point five.
(iii) 0.02 = zero point zero two, 0.56 = zero point five six, 13.06 = thirteen point zero six.
(iv) 0.005 = zero point zero zero five, 0.207 = zero point two zero seven, 111.519 = one hundred eleven point five one nine.
(v) 0.8 = zero point eight, 0.08 = zero point zero eight, 0.008 = zero point zero zero eight, 0.0008 = zero point zero zero zero eight
(vi) 256.1 = Two hundred fifty six point one, 10.22 = Ten point two two, 0.634 = zero point six three four.

Question 5.
Convert the given fractions into like fractions:
(i) 0.5,3.62,43.987 and 232.0037
(ii) 215.78, 33.0006, 530.3 and 0.03569

Answer:
(i) 0.5, 3.62, 43.987 and 232.0037
In these decimals, the greatest places of decimal is 4
∴0.5 = 0.5000
3.62 = 3.6200
43.987 = 43.9870
232.0037 = 232.0037

(ii) 215.78, 33.0006, 530.3 and 0.03569
In these decimals, the greatest places of decimal is 5
∴215.78 = 215.78000
33.0006 = 33.00060
530.3 = 530.30000
0.03569 = 0.03569

Decimal Fractions Exercise 4B – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Add:
(i) 0.5 and 0.37 (ii) 3.8 and 8.7
(iii) 0.02, 0.008 and 0.309
(iv) 0. 4136, 0. 3195 and 0.52
(v) 9.25, 3.4 and 6.666
(vi) 3.007, 0.587 and 18.341
(vii) 0.2, 0.02 and 2.0002
(viii) 6. 08, 60.8, 0.608 and 0.0608
(ix) 29.03, 0.0003, 0.3 and 7.2
(x) 3.4, 2.025, 9.36 and 3.6221

Answer:

Question 2.
Subtract the first! number from the second :
(i) 5.4, 9.8
(ii) 0.16, 4.3
(iii) 0.82, 8.6
(v) 2.237, 9.425
(vi) 41 .03, 59.46
(vii) 3.92. 26.86
(viii) 4.73, 8.5
(ix) 12.63, 36.2
(x) 0.845, 3.71

Answer:

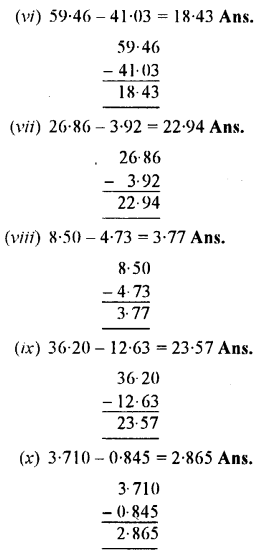
Question 3.
Simplify :
(i) 28.796 -13.42 – 2.555
(ii) 93.354 – 62.82 – 13.045
(iii) 36 – 18.59 – 3.2
(iv) 86 + 16.95 – 3.0042
(v) 32.8 – 13 – 10.725 +3.517
(vi) 4000 – 30.51 – 753.101 – 69.43
(vii) 0.1835 + 163.2005 – 25.9 – 100
(viii) 38.00 – 30 + 200.200 – 0.230
(ix) 555.555 + 55.555 – 5.55 – 0.555

Answer:

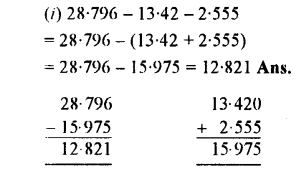
Question 4.
Find the difference between 6.85 and 0.685.
Answer:

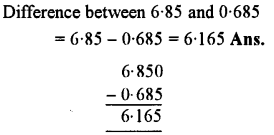
Question 5.
Take out the sum of 19.38 and 56.025 then subtract it from 200. 111.
Answer:

Question 6.
Add 13.95 and 1.003 ; and from the result, subtract the sum of 2.794 and 6.2.
Answer:

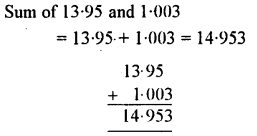
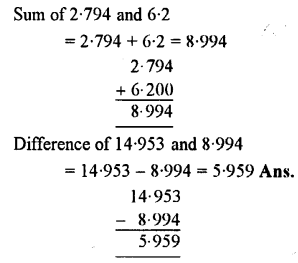
Question 7.
What should be added to 39.587 to give 80.375 ?

Answer:

Question 8.
What should be subtracted from 100 to give 19.29?
Answer:

Question 9.
What is the excess of 584.29 over 213.95 ?
Answer:

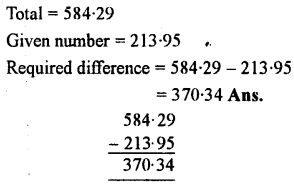
Question 10.
Evaluate:
(i) (5.4 – 0.8) + (2.97 -1.462)
(ii) (6.25 + 0.36) -(17.2 – 8.97)
(iii) 9.004 + (3 -2.462)
(iv) 879.4 – (87.94 – 8 .794)

Answer:

Question 11.
What is the excess of 75 over 48.29?
Answer:

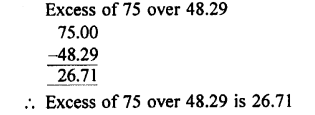
Question 12.
If A = 237.98 and B = 83.47.
Find :
(i) A – B
(ii) B – A.
Answer:

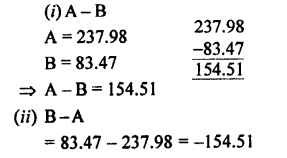
Question 13.
The cost of one kg of sugar increases from ?28.47 to T32.65. Find the increase in cost.

Answer:

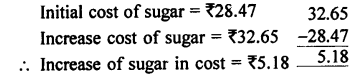
Decimal Fractions Exercise 4C – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Multiply:
(i) 0.87 by 10
(ii) 2.948 by 100
(iii) 6.4 by 1000
(iv) 5.8 by 4
(v) 16.32 by 28
(vi) 5. 037 by 8
(vi) 4.6 by 2.1
(viii) 0.568 by 6.4

Answer:

Question 2.
Multiply each number by 10, 100, 1000 :
(i) 0.5
(ii) 0.112
(iii) 4.8
(iv) 0.0359
(v) 16.27
(vi) 234.8

Answer:
(i) 0.5 x 10 = 5,0.5 x 100 = 50,
0.5 x 1000 = 500
(ii) 0.112 x 10= 1.12,0.112 x 100
= 11.2, 0.112 x 1000= 112
(iii) 4.8 x 10 = 48, 4.8 x 100 = 480,
4.8 x 1000 = 4800
(iv) 0.0359 x 10 = 0.359,0.0359 x 100 = 3.59, 0.0359 x 1000 = 35-9
(v) 16.27 x 10 = 162.7, 16.27 x 100 = 1627, 16.27 x 1000= 16270
(vi) 234.8 x 10 = 2348, 234.8 x 100 = 23480, 234.8 x 1000 = 234800

Question 3.
Evaluate:
(i) 5.897 x 2.3
(ii) 0.894 x 87
(iii) 0.01 x 0.001
(iv) 0.84 x 2.2 x 4
(v) 4.75 x 0.08 x 3
(vi) 2.4 x 3.5 x 4.8
(vii) 0.8 x 1.2 x 0.25
(viii) 0.3 x 0.03 x 0.003
(ix) 12.003 x (0.2)5

Answer:

Question 4.
Divide :
(i) 54.9 by 10
(ii) 7.8 by 100
(iii) 324.76 by 1000
(iv) 12.8 by 4
(v) 27.918 by 9
(vi) 4.672 by 8
(vii) 4.32 by 1.2
(viii) 7.644 by 1.4
(ix) 4.8432 by 0.08

Answer:

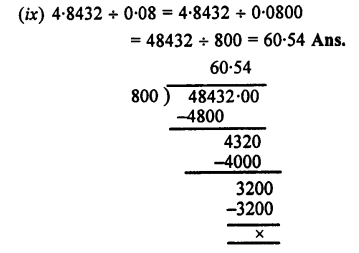
Question 5.
Divide each of the given numbers by 10, 100, 1000 and 10000
(i) 2.1
(ii) 8.64
(iii) 5-01
(iv) 0.0906
(v) 0.125
(vi) 111.11
(vii) 0.848 x 3
(viii)4.906 x (0.2) ²
(ix) (1.2)² x(0.9)²

Answer:

(i) 2.1 ÷ 10 = 0.21, 2.1 ÷ 100 = 0.021,
2.1 ÷ 1000 = 0.0021
and 2.1 ÷10000 = 0.00021

(ii) 8.64 ÷ 10 = 0-864, 8.64 ÷ 100 = 0-0864,
8.64 ÷ 1000 = 0-00864
and 8.64 ÷ 10000 = 0.000864

(iii)5.01 ÷ 10 = 0.501,
5.01 ÷ 100 = 0.0501,
5.01 ÷1000 = 0.00501,
5.01 ÷ 10000 = 0.000501

(iv) 0.0906 ÷ 10 = 0.00906,
0.0906 ÷ 100 = 0.000906,
0.0906 ÷ 1000 = 0.0090906,
0.0906 ÷ 10000 = 0.00000906

(v) 0.125
Now 0.125 + 10 = 0.0125,
0.125 ÷ 100 = 0-00125,
0.125 ÷1000 = 0.000125,
0.125 ÷ 10000 = 0.0000125

(vi) 111.11÷ 10= 11.111,
111.11÷ 100 = 1.1111,
111.11 ÷ 1000 = 0.11111,
111.11 ÷ 10000 = 0.011111

(vii) 0.848 x 3 = 2.544 ,
Now 2.544 ÷ 10 = 0.2544,
2.544 ÷ 100 = 0-02544,
2-544 ÷ 1000 = 0-002544,
2-544 ÷ 10000 = 0-0002544

(viii) 4.906 x (0.2)² = 4.906 x 0.2 x 0.2
= 4.906 x 0.04 = 0.19624
Now 0.19624 + 10 = 0.019624,
0.19624 + 100 = 0.0019624,
0.19624 + 1000 = 0.00019624,
0.19624 + 10000 = 0.000019624

(ix) (1.2)² x (0.9)² = 1.2 x 1.2 x 0.9 x 0.9 = 1.44 x 0.81 = 1.1664
Now 1 .1664 + 10 = 0.11664,
1.1664 ÷ 100 = 0.011664,
1.1664 ÷ 1000 = 0.0011664,
1.1664 ÷ 10000 = 0.00011664

Question 6.
Evaluate :
(i) 9.75 + 5
(ii) 4.4064 + 4
(iii) 27.69 + 30
(iv) 19.25 + 25
(v) 20.64+ 16
(vi) 3.204 + 9
(vii) 0.125 + 25
(viii) 0.14616 + 72
(ix) 0.6227+ 1300
(x) 257.894+ 0-169
(xi) 6.3 + (0.3)²

Answer:

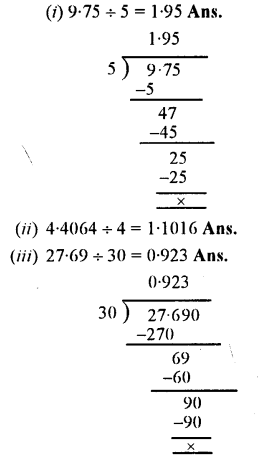
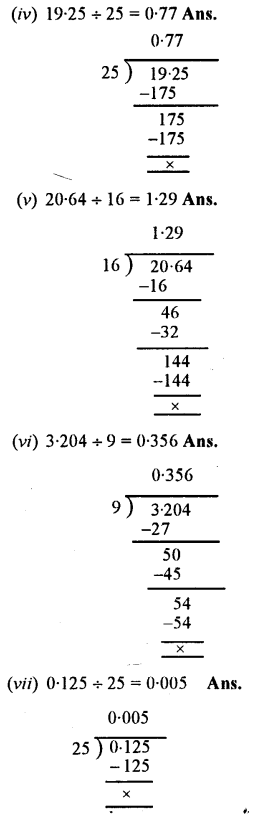
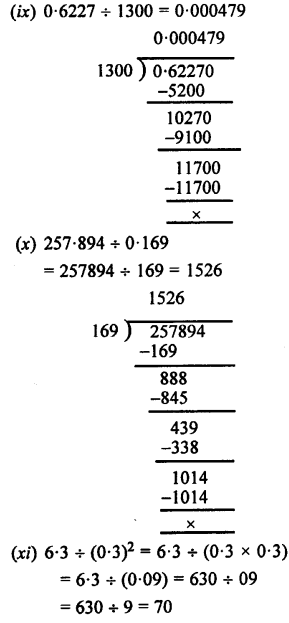
Question 7.
Evaluate:
(i) 4.3 x 0.52 x 0.3
(ii) 3.2 x 2.5 x 0.7
(iii) 0.8 x 1.5 x 0.6
(iv) 0.3 x 0.3 x 0.3
(v) 1.2 x 1.2 x 0.4
(vi) 0.4 x 0.04 x 0.004
(vii) 0.5 x 0.6 x 0.7
(Viii) 0.5 x 0.06 x 0.007

Answer:

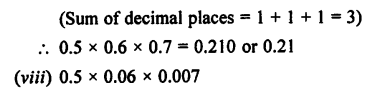
Question 8.
Evaluate:
(i) (0.9)²
(ii) (0.6)² x 0.5
(iii) 0.3 x (0.5)²
(iv) (0.4)³
(v) (0.2)³ x 5
(vi) (0.2)³ x 0.05

Answer:

(i) (0.9)²
⇒ 0.9 x 0.9 = 0.81
(Sum of decimal places 1 + 1=2)

(ii) (0.6)² x 0.5
⇒ 0.6 x 0.6 x 0.5
⇒ 0.36 x 0.5 = 0.180 or 0.18
(Sum of decimal places = 1 + 1 + 1 = 3)

(iii) 0.3 x (0.5)²
⇒ 0.3 x 0.5 x 0.5
⇒ 0.3 x 0.25 = 0.075
(Sum of decimal places 1 + 1 + 1 = 3)
(iv) (0.4)³
⇒ 0.4 x 0.4 x 0.4
⇒ 0.16 x 0.4 = 0.064
(Sum of decimal places 1 + 1 + 1 = 3)

(v) (0.2)³ x 5
⇒ 0.2 x 0.2 x 0.2 x 5
⇒ 0.08 x 5 = 0.40 or 0.4
(Sum of decimal places 1 + 1 + 1 = 3)

(vi) (0.2)³ x 0.05
⇒ 0.2 x 0.2 x 0.2 x 0.05
⇒ 0.008 x 0.05 = 0.00040
(Sum of decimal places = 5)

 Question 9.
Find the cost of 36.75 kg wheat at the rate of ₹12.80 per kg.
Answer:

Question 10.
The cost of a pen is ₹56.15. Find the cost of 16 such pens.
Answer:

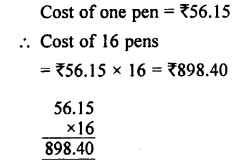
Question 11.
Evaluate:
(i) 0.0072 ÷ 0.06
(ii) 0.621 ÷ 0.3
(iii) 0.0532 ÷ 0.005
(iv) 0.01162 ÷ 0.14
(v) (7.5 x 40.4) ÷ 25
(vi) 2.1 ÷ (0.1 x 0.1)

Answer:

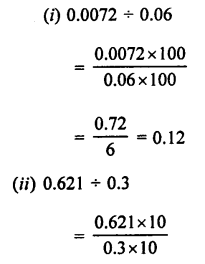
Question 12.
Fifteen indentical articles weigh 31.50 kg. Find the weight of each article.
Answer:
Weight of 15 articles = 31.50 kg
∴ Weight of one article
= 31.50- 15 = 2.1 kg

Question 13.
The product of two numbers is 211.2. If one of these two numbers is 16.5, find the other number.
Answer:

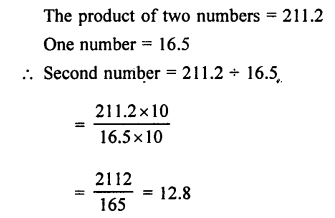
Question 14.
One dozen identical articles cost ₹45.96. Find the cost of each article.
Answer:
∴ Weight of one dozen articles = ₹45.96
One dozen = 12
∴ Cost of one article = 45.96 + 12 = ₹3.83

Decimal Fractions Exercise 4D – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Find whether the given division forms a terminating decimal or a non-terminating decimal:
(i) 3 ÷ 8
(ii)8 ÷ 3
(iii) 6÷ 5
(iv) 5 ÷ 6
(v) 12.5 ÷ 4
(vi) 23 ÷ 0.7
(vii) 42 ÷ 9
(viii) 0.56÷ 0.11

Answer:

Question 2.
Express as recurring decimals :

Answer:

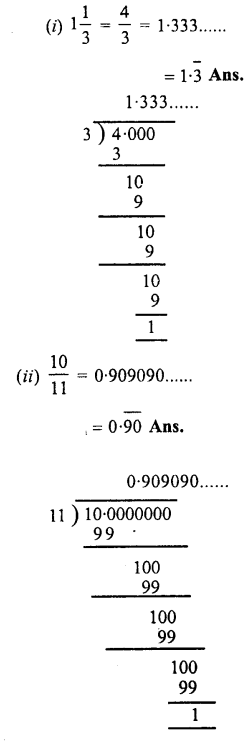
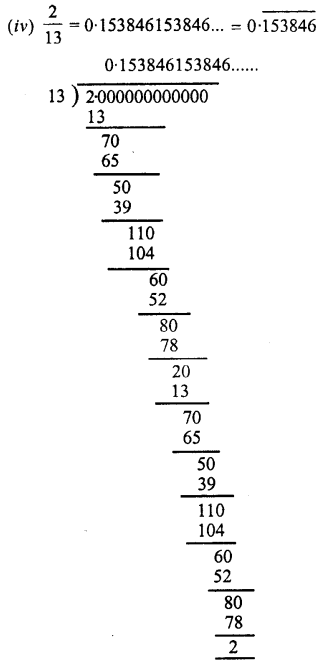
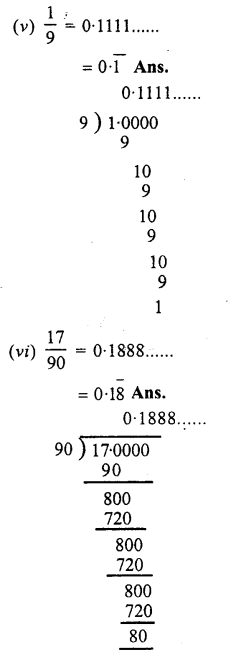
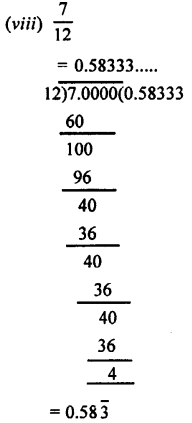
Question 3.
Convert into vulgar fraction :
(i) 0.\(\bar { 3 }\)
(ii) 0.\(\bar { 8 }\)
(iii) 4.\(\bar { 4 }\)
(iv) 23.\(\bar { 7 }\)

Answer:

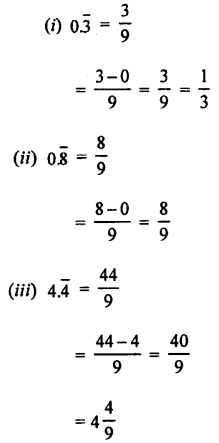
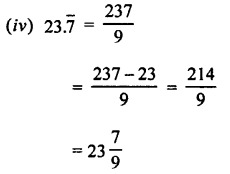
Question 4.
Convert into vulgar fraction :
(i) 0.\(\bar { 35 }\)
(ii) 2.\(\bar { 23 }\)
(iii) 1.\(\bar { 28 }\)
(iv) 5.\(\bar { 234 }\)

Answer:

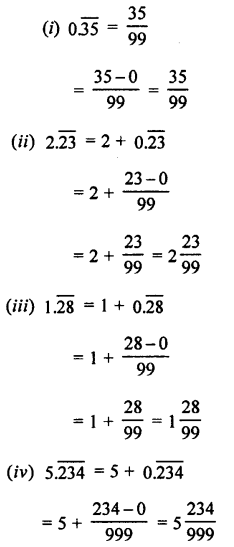
Question 5.
Convert into vulgar fraction :
(i) 0 0.3\(\bar { 7 }\)
(ii) 0.2\(\bar { 45 }\)
(iii) 0.68\(\bar { 5 }\)
(iv) 0.4\(\bar { 42 }\)

Answer:

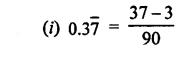
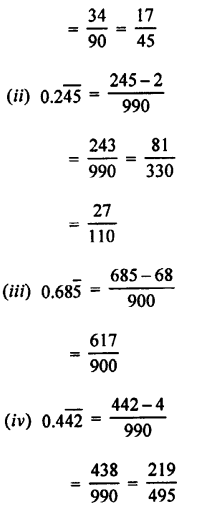
Decimal Fractions Exercise 4E – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
Round off:
(i) 0 .07, 0.112, 3.59, 9.489 to the nearest tenths.
(ii) 0.627, 100.479, 0 065 and 0.024 to the nearest hundredths.
(iii) 4.83,0.86,451 .943 and 9.08 to the nearest whole number.

Answer:
(i) 0.07 = 0.1,
0.112 = 0.1
3 . 59 = 3.6, 9.489 = 9.5
(ii) 0.627 = 0.63,
100.479 = 100.48
0.065 = 0.07,
0.024 = 0.02
(iii) 4.83 = 5,
0.86= 1,
451.943 = 452
9.08 = 9

Question 2.
Simplify, and write your answers correct to the nearest hundredths :
(i) 18 .35 x 1.2
(ii) 62.89 x 0.02

Answer:

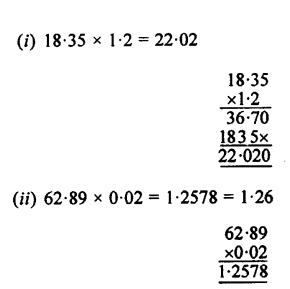
Question 3.
Write the number of significant figures (digits) in:
(i) 35.06
(ii) 0.35
(iii) 7.0068
(iv) 19 .0
(v) 0.0062
(vi) 0 4.2 x 0.6
(vii) 0.08 x 25
(viii) 3.6 ÷ 0.12 .

Answer:
(i) 35.06 : In this significant figures i.e. digits are 4
(ii) In 0.35, significant figures are 2
(iii) In 7.0068, significant figures are 5
(iv) In 19.0, significant figures are 3
(v) In 0.0062, significant figures are 2
(vi) In 4.2 x 0.6 = 2.52, significant figure are 3
(vii) In 008 x 25 = 2.00 = 2 significant figure is 1
(viii) In 3.6 ÷0 .12 or 360 ÷ 12 = 30, significant figure are 2.

Question 4.
Write :
(i) 35.869,0 008426,4.952 and 382.7, correct lo three significant figures.
(ii) 60.974. 2.8753, 0.001789 and 400.04, correct to four significant figures.
(iii) 14.29462, 19.2, 46356.82 and 69, correct to five significant figures.

Answer:
(i) Correct to three significant figures are
35.869 → 35.9
0.008426 →0.00843
4. 952→ 4.95
382.7 →383
(ii) Correct to four significant figures
60.974 →60.97
2. 8753 → 2.875
0.001789 → 0.001789
400.04 → 400.0
(iii) Correct to five significant figures
14.29462→ 14.295
19.2 → 19.200
46356.82 →46357
69 → 69.000

Decimal Fractions Exercise 4F – Selina Concise Mathematics Class 7 ICSE Solutions

Question 1.
The weight of an object is 3 .06 kg. Find the total weight of 48 similar objects.

Answer:

Question 2.
Find die cost of 17.5 m cloth at the rate of Rs. 112.50 per metre.

Answer:

Question 3.
One kilogramme of oil costs Rs. 73.40. Find the cost of 9.75 kilogramme of the oil.

Answer:

Question 4.
Total weight of 8 identical objects is 51.2 kg. Find the weight of each object.
Answer:
Weight of 8 objects = 51-2 kg
∴ Weight of 1 object = 51 -2 + 8 kg = 6-4 kg Ans.

Question 5.
18.5 m of cloth costs Rs. 666. Find the cost of 3.8 m cloth.

Answer:
Cost of 18.5 m cloth = Rs. 666
Cost of 1 m cloth = Rs. 666 ÷18.5 and cost of 3.8 m cloth
= Rs. (666 ÷18.5) x 3-8 = Rs. (6660 ÷ 185) x 3.8 = Rs. 36 x 3.8 = Rs. 136.80

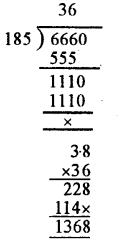
Question 6.
Find die value of:
(i) 0.5 of Rs. 7.60 + 1.62 of Rs. 30
(ii) 2.3 of 7.3 kg + 0.9 of 0.48 kg
(iii) 6.25 of 8.4 – 4.7 of 3.24
(iv) 0.98 of 235 – 0 .09 of 3.2

Answer:

Question 7.
Evaluate:
(i) 5.6 – 1 .5 of 3.4
(ii) 4.8 ÷ 0.04 of 5
(iii) 0.72 of 80 + 0.2
(iv) 0.72 ÷ 80 of 0.2
(v) 6.45 + (3.9 – 1.75)
(vi) 0.12 of(0.104 – 0.02)+ 0.36 x 0.5

Answer: