NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.4 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 6 Triangles Class 10 NCERT Solutions Ex 6.4.
- Triangles Class 10 Ex 6.1
- Triangles Class 10 Ex 6.2
- Triangles Class 10 Ex 6.3
- Triangles Class 10 Ex 6.5
- Triangles Class 10 Ex 6.6
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Chapter Name | Triangles |
| Exercise | Ex 6.4 |
| Number of Questions Solved | 9 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.4
NCERT Solutions for Class 10 Maths
Page No: 143
Question 1. Let ΔABC ~ ΔDEF and their areas be, respectively, 64 cm2 and 121 cm2. If EF = 15.4 cm, find BC.
Solution:

Question 2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Solution:
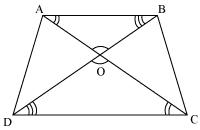
Since AB || CD
∠OAB = ∠OCD (Alternate interior angles)
∠OBA = ∠ODC (Alternate interior angles)
∠AOB = ∠COD (Vertically opposite angles)
Therefore ∆AOB ~ ∆COD (By AAA rule)

Question 3. In the fig 6.53, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that area ![]()
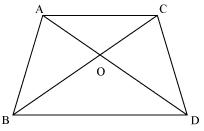
Solution:
We know that area of a triangle = 1/2 × Base × height
Since ∆ABC and ∆DBC are one same base,
Therefore ratio between their areas will be as ratio of their heights.
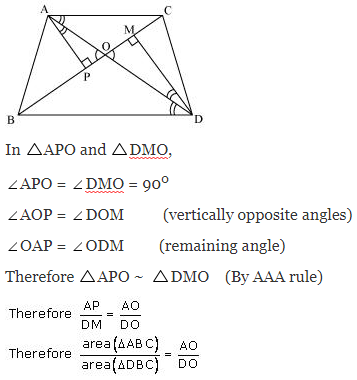
Let us draw two perpendiculars AP and DM on line BC.
Question 4. If the areas of two similar triangles are equal, prove that they are congruent.
Solution:
Let us assume two similar triangles as ∆ABC ~ ∆PQR

Question 5. D, E and F are respectively the mid-points of sides AB, BC and CA of ΔABC. Find the ratio of the area of ΔDEF and ΔABC.
Solution:
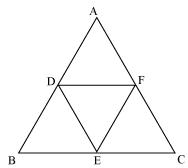
Since D and E are mid points of ∆ABC

Question 6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:
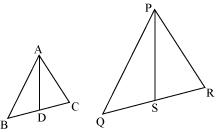
Let us assume two similar triangles as ∆ABC ~ ∆PQR. Let AD and PS be the medians of these triangles.
![]()
∠A = ∠P, ∠B = ∠Q, ∠C = ∠R
Since, AD and PS are medians

Question 7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:
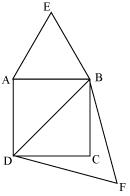
Let ABCD be a square of side a.
Therefore its diagonal = √2a
Two desired equilateral triangles are formed as ∆ABE and ∆DBF
Side of an equilateral triangle ∆ABE described on one of its side = a
Side of an equilateral triangle ∆DBF described on one of its diagonal
We know that equilateral triangles are having all its angles as 60º and all its sides of same length. So, all equilateral triangles are similar to each other. So, ratio between areas of these triangles will be equal to the square of the ratio between sides of these triangles.
![]()
8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the area of triangles ABC and BDE is
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
Solution:
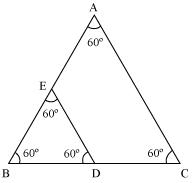
We know that equilateral triangles are having all its angles as 60º and all its sides of same length. So, all equilateral triangles are similar to each other. So, ratio between areas of these triangles will be equal to the square of the ratio between sides of these triangles.
Let side of ∆ABC = x
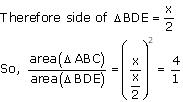
Hence, (c)
Question 9. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
Solution:
If, two triangles are similar to each other, ratio between areas of these triangles will be equal to the square of the ratio between sides of these triangles.
Given that sides are in the ratio 4:9.
So, ratio between areas of these triangles \(=\left( \frac { 4 }{ 9 } \right) ^{ 2 }=\frac { 16 }{ 81 } \)
Hence, (d).
We hope the NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.4 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.4, drop a comment below and we will get back to you at the earliest.