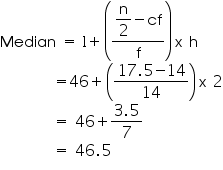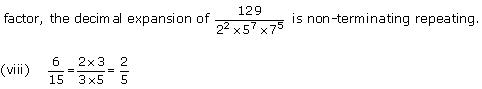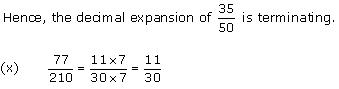NCERT Solutions for Class 10 Maths Archives

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1

September 18, 2021September 18, 2021 by Raju

Are you looking for the best Maths NCERT Solutions Chapter 3 Ex 3.1 Class 10? Then, grab them from our page and ace up your preparation for CBSE Class 10 Exams.

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 3 Pair of Linear Equations in Two Variables Class 10 NCERT Solutions Ex 3.1.

NCERT Solutions for Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables are provided here with simple step-by-step explanations. These solutions for Pair Of Linear Equations In Two Variables are extremely popular among class 1 0 students for Math Pair Of Linear Equations In Two Variables Solutions come handy for quickly completing your homework and preparing for exams.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 3
Chapter Name	Pair of Linear Equations in Two Variables
Exercise	Ex 3.1
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1

Page No: 44

Question 1. Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” (Isn’t this interesting?) Represent this situation algebraically and graphically.

Solution:
Let the present age of Aftab and his daughter be x and y respectively.
Seven years ago,
Age of Aftab = x – 7
Age of his daughter = y – 7
According to the given condition,
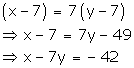
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables 1

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables 1

Three years hence,
Age of Aftab = x + 3
Age of his daughter = y + 3
According to the given condition,

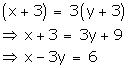
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables 2

Thus, the given conditions can be algebraically represented as:
x – 7y = -42
x – 3y = 6
x – 7y = -42 ⇒ × = -42 + 7y
Three solutions of this equation can be written in a table as follows:

x	-7	0	7
y	5	6	7

× -3y = 6 ⇒ × = 6 + 3y
Three solutions of this equation can be written in a table as follows:

x	6	3	0
y	0	-1	-2

The graphical representation is as follows:
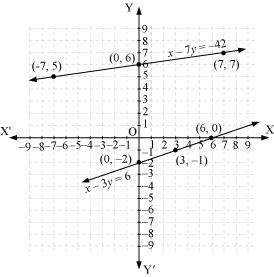
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables 3

Concept Insight: In order to represent a given situation mathematically, first see what we need to find out in the problem. Here, Aftab and his daughter’s present age needs to be found so, so the ages will be represented by variables x and y. The problem talks about their ages seven years ago and three years from now. Here, the words ‘seven years ago’ means we have to subtract 7 from their present ages, and ‘three years from now’ or ‘three years hence’ means we have to add 3 to their present ages. Remember in order to represent the algebraic equations graphically the solution set of equations must be taken as whole numbers only for the accuracy. Graph of the two linear equations will be represented by a straight line.

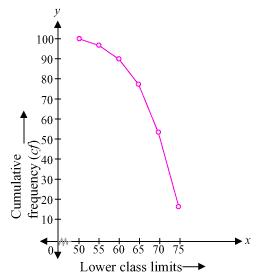
Question 2. The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and 3 more balls of the same kind for Rs 1300. Represent this situation algebraically and geometrically.

Solution:
Let the cost of a bat and a ball be Rs x and Rs y respectively.
The given conditions can be algebraically represented as:
3x + 6y = 3900
x + 2y = 1300

Three solutions of this equation can be written in a table as follows:

x	300	100	-100
y	500	600	700

x + 2y = 1300 ⇒ x = 1300 – 2y
Three solutions of this equation can be written in a table as follows:

x	300	100	-100
y	500	600	700

The graphical representation is as follows:

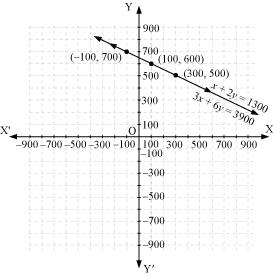
Concept Insight:Cost of bats and balls needs to be found so the cost of a ball and bat will be taken as the variables. Applying the conditions of total cost of bats and balls algebraic equations will be obtained. Then, in order to represent the obtained equations graphically take atleast three ordered pairs on both the equations in order to avoid any computational errors.

Question 3. The cost of 2 kg of apples and 1kg of grapes on a day was found to be Rs 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs 300. Represent the situation algebraically and geometrically.

Solution:
Let the cost of 1 kg of apples and 1 kg grapes be Rs. x and Rs. y.
The given condtions can be algebraically represented as:
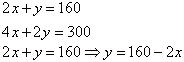
NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables 6
Three solutions of this equation can be written in a table as follows:

x	50	60	70
y	60	40	20

Three solutions of this equation can be written in a table as follows:

x	70	80	75
y	10	-10	0

The graphical representation is as follows:

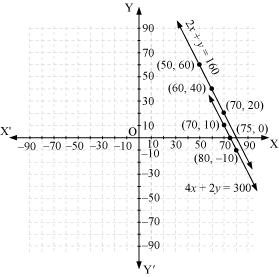
Concept Insight: cost of apples and grapes needs to be found so the cost of 1 kg apples and 1 kg grapes will be taken as the variables. From the given conditions of collective cost of apples and grapes, a pair of linear equations in two variables will be obtained. Then, in order to represent the obtained equations graphically, take the values of variables as whole numbers only. Since these values are large so take the suitable scale like 1 cm = 20.

NCERT Solutions For Class 10 Maths – AplusTopperhttps://t.co/q7hSKh3xmf #NCERTSolutionsForClass10Maths #NCERTSolutions #AplusTopper
— ObulReddy cbse (@ObulReddyCBSE) August 3, 2018

We hope the NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 10 Maths

July 30, 2021July 30, 2021 by Veerendra

NCERT Solutions for Class 10 Maths

NCERT Solutions for Class 10 Maths: As a student, it becomes difficult to solve some of the questions given in the textbook. There are solved examples at the start of the chapter that can you help understand the method to solve the question. But many times the practice questions can be very tiresome. There have been many cases where students have found it very difficult to solve the practice questions. One particular subject that has this problem is maths. Thus, we are providing you with NCERT solutions for class 10 Maths. This article will help you with all the chapters and their solutions so that you can understand them better and prepare well for the exams.

Teachers at APlusTopper.com solved NCERT Solutions for Class 10 Maths. Class 10 Maths NCERT Solutions are of great help in completing homework and clearing your doubts. All these from NCERT book For class 10 Maths have been solved keeping in mind the guidelines issued by the CBSE.

NCERT Solutions for Class 10 Maths

Class 10 is very important for students as this is the first time students will be appearing for a board exam. This also makes up for a whole new experience for the students. Thus, students become conscious and try and solve every question given in the textbook. So, a thorough knowledge of all the chapters in the textbook becomes a priority for everyone. This NCERT solution provided for class 10 maths can help you with this. It will also help you prepare the subject in very less time. We will try to go in detail for each and every chapter. Many of the topics for class 10 areas an extension to class 9. Thus, you don’t need to worry too much about the content. Rather just practice all the questions given in the textbook.

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers

NCERT Solutions for Class 10 Maths Chapter 2 Polynomials

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

NCERT Solutions for Class 10 Maths Chapter 4 Quadratic Equations

NCERT Solutions for Class 10 Maths Chapter 5 Aritthmetic Progressions

NCERT Solutions for Class 10 Maths Chapter 6 Triangles

NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry

NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Tringonmetry

NCERT Solutions for Class 10 Maths Chapter 9 Some Applications of Trigonometry

Some Applications of Trigonometry Class 10 Ex 9.1

NCERT Solutions for Class 10 Maths Chapter 10 Circles

NCERT Solutions for Class 10 Maths Chapter 11 Constructions

NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles

NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes

NCERT Solutions for Class 10 Maths Chapter 14 Statistics

NCERT Solutions for Class 10 Maths Chapter 15 Probability

Maths NCERT Solutions class 10 has also been done in accordance with the marking scheme usually followed by the CBSE Board. AplusToper.com sincerely hope that NCERT Class 10 Maths Solutions will be an effective tool in the hands of the students preparing for their CBSE Board Exams.

Class 10 Maths Real Numbers Solutions

Most of this ncert maths chapter follows the content that you have learned in class 9. The important properties for this chapter are covered in section 1.2 and 1.3. These properties are the fundamental theorem of arithmetic and Euclid’s division algorithm. Besides this, you will relearn the irrational numbers in section 1.4. Also, decimal expressions of rational numbers are included in section 1.5. There are a plethora of applications that are associated with Euclid’s division algorithm. Mostly this algorithm deals with the divisibility of the integers. Also, it deals with the divisibility of the integers. This chapter 1 in NCERT will be helpful for calculating the HCF of two positive integers.

Class 10 Maths Chapter 2 Polynomials Solutions

There are a total of four exercises in polynomials. The last exercise of the four is optional. Every exercise given in this chapter is solved using different methods. You need to find the number of zeroes in p(x) polynomial in the first exercise. While there are two questions in the second exercise. As mentioned above, you need to find a relationship between the coefficient and zeroes in the first exercise. And in the second you have to find a quadratic polynomial. There are a total of five questions in the third exercise. In this, you need to divide polynomials and thereby obtain the number of zeroes in the polynomials. The optional exercise which is the last one also has five questions in it.

Class 10 Maths Chapter 3 Linear Equation in Two Variables Solutions

The basics of this topic were discussed in class 9. While in class 10, this topic goes into more complex scenarios. There are a total of seven exercises in this chapter for students to practice. Some of the important topics that are covered in this chapter are a pair of linear equations in 2 variables, graphical representations, solving a pair of linear equations using algebraic methods, and elimination method. Also, some of the topics in this chapter are substitution method, cross-multiplication method and graphical method for the solution of linear equations.

Class 10 Maths Chapter 4 Quadratic Equations Solutions

In this chapter, you will study quadratic equations in depth. Furthermore, you will study to find the roots of quadratic equations. There are also some of the daily life applications of quadratic equations in this chapter. A total of 4 exercises are there in this chapter. There are two questions in the first exercise where you need to find whether the equations are quadratic or not. In the second you will be given daily life examples that need to be converted into quadratic equations. Also, in the second exercise, you are asked to find the roots of quadratic equations using factorization. The main topics in this chapter are solutions by factorization and solutions of a quadratic equation using the square.

Class 10 Maths Chapter 5 Arithmetic Progression Solutions

This chapter has some daily life examples and then it gradually moves towards the complexities of the chapter. There are four exercises described in the chapter. These exercises are divided further into various questions where you need to find a term. In this chapter, you will learn how to find the nth term. Alongside you will also find the sum of n consecutive terms.

Class 10 Maths Chapter 6 Triangles Solutions

This is one of the biggest chapters in CBSE Syllabus. This is because it has six exercises on it. There are different questions in each exercise that are based on the properties of the triangle. It consists of 9 theorems in total. Thus, this is one of the important chapters in maths for class 10.

Class 10 Maths Chapter 7 Coordinate Geometry Solutions

The questions in this chapter are mostly based on finding the distances between two points. There are coordinates provided along with the triangle. The area of the triangle is found using these three points. This chapter has a total of four exercises in it.

Class 10 Maths Chapter 8 Trigonometry Solutions

This chapter is mainly on finding the trigonometric ratios for a side of the right angled triangle. These ratios are called trigonometric ratios. There are a total of 4 exercises in this chapter. The main topics covered in this chapter are trigonometric ratios, trigonometric identities, trigonometric ratios for complementary angles, and for specific angles.

Class 10 Maths Chapter 9 Applications of Trigonometry Solutions

There is only one exercise in this chapter and the questions are mostly related to the practical applications of trigonometry. You will also study interesting ways to use trigonometry in real life.

Class 10 Maths Chapter 10 Circles Solutions

There are only two exercises in a circle. First one has the basic questions related to circles. While in the second one you need to find various ways to prove the given equations.

Class 10 Maths Chapter 11 Constructions Solutions

In this chapter, you have found various constructions like constructions of tangents to a circle, division of line segment, etc. It has two exercises and the questions are related to them only.

Class 10 Maths Chapter 12 Areas of a Circle Solutions

In this chapter, you need to find the areas of a circle. Furthermore, you are also required to find the areas of ‘special’ parts of a circle. This chapter has three exercises.

Class 10 Maths Chapter 13 Surface Area and Volume Solutions

This chapter deals with problems of finding surface areas and volumes of various cubes, cylinder, and cuboid. There are a total of five exercises in this for students to practice.

Class 10 Maths Chapter 14 Statistics Solutions

This chapter mainly deals with finding the mean, median, and mode. The data given can be grouped or ungrouped. For your practice, there are a total of 4 exercises. There are also questions related to cumulative frequency in this chapter. Furthermore, this chapter covers topics like cumulative frequency distribution and drawing cumulative frequency curves.

Class 10 Maths Chapter 15 Probability Solutions

The chapter deals mainly with finding the probability of daily situations. This is mostly related to dices and coins.

We have tried to give you an overview of what NCERT chapters have. There are many exercises in the book for you to practice. You can follow the website for NCERT class 10 maths solutions and other updates. Hope given NCERT Solutions for Class 10 Maths helpful to finish your Home Work. If you find these solutions helpful, Please share with your friends.

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2

November 27, 2020September 4, 2020 by Dattu

In this article, we have provided step by step Chapter 5 Ex 5.2 Class 10 Maths NCERT Solutions.

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2 are part of
NCERT Solutions for Class 10 Maths. Here are we have given Chapter 5 Arithmetic Progressions Class 10 NCERT Solutions Ex 5.2.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 5
Chapter Name	Arithmetic Progressions
Exercise	Ex 5.2
Number of Questions Solved	20
Category	NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2

You can also Read Latest NCERT Solutions for Class 10 Maths Chapter-wise to help you to revise the complete Syllabus and score more marks in your examinations.

Page No: 105

Question 1. Fill in the blanks in the following table, given that a is the first term, d the common difference and a_n the n^th term of the A.P.
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 67

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 6

Question 2. Choose the correct choice in the following and justify
(i) 30^th term of the A.P: 10, 7, 4, …, is
(A) 97 (B) 77 (C) −77 (D.) −87

(ii) 11^thterm of the A.P. -3, -1/2, ,2 …. is
(A) 28 (B) 22 (C) – 38 (D) -48×1/2

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 7

Question 3. In the following APs find the missing term in the boxes.
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 8

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 9

Question 4. Which term of the A.P. 3, 8, 13, 18, … is 78?

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 10

Question 5. Find the number of terms in each of the following A.P.

Solution :
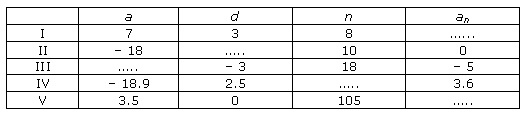
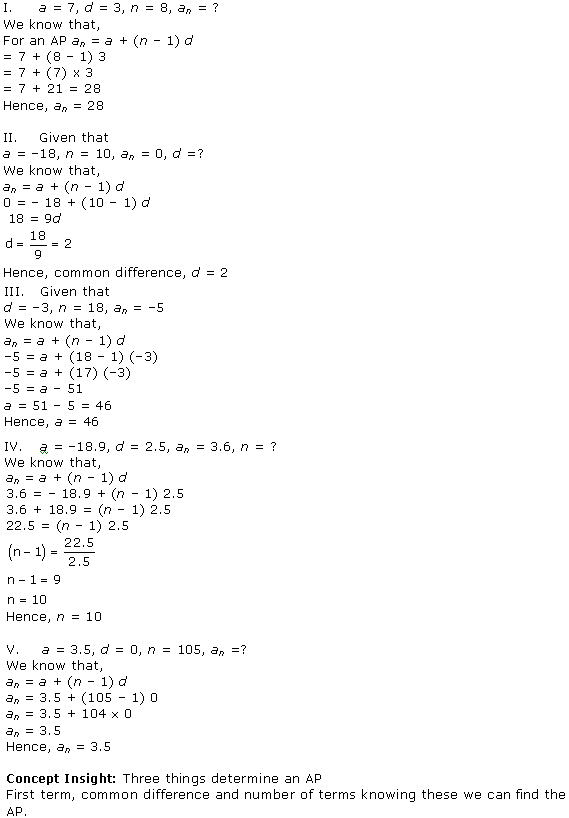
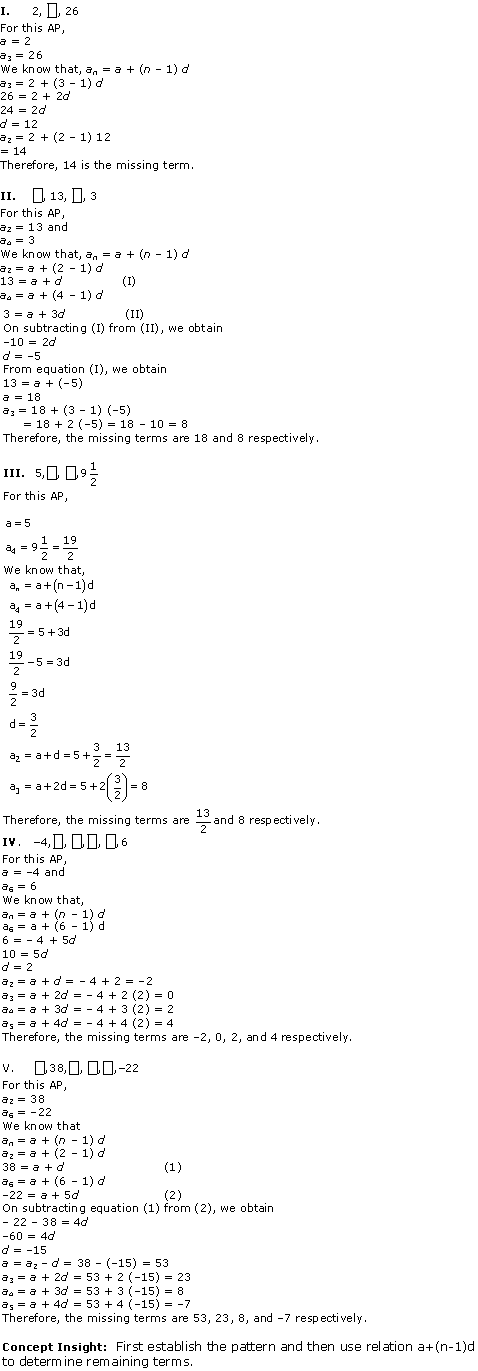
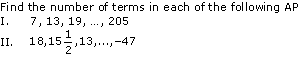
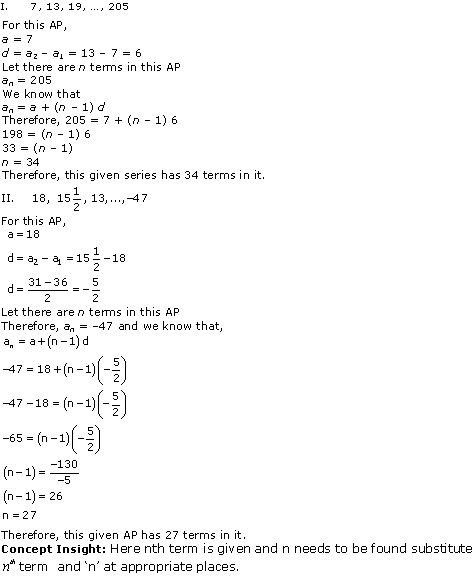
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 12

Question 6. Check whether -150 is a term of the A.P. 11, 8, 5, 2, …

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 13

Question 7. Find the 31^st term of an A.P. whose 11^th term is 38 and the 16^thterm is 73.

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 14

Question 8. An A.P. consists of 50 terms of which 3^rd term is 12 and the last term is 106. Find the 29^th term.

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 15

Question 9. If the 3^rd and the 9^th terms of an A.P. are 4 and − 8 respectively. Which term of this A.P. is zero.

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 16

Question 10. If 17^th term of an A.P. exceeds its 10^th term by 7. Find the common difference.

Solution :
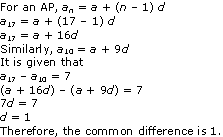
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 17

Question 11. Which term of the A.P. 3, 15, 27, 39, … will be 132 more than its 54^th term?

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 18

Question 12. Two APs have the same common difference. The difference between their 100^th term is 100, what is the difference between their 1000^th terms?

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 19

Question 13. How many three digit numbers are divisible by 7?

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 20

Question 14. How many multiples of 4 lie between 10 and 250?

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 21

Question 15. For what value of n, are the n^th terms of two APs 63, 65, 67, and 3, 10, 17, … equal?

Solution :
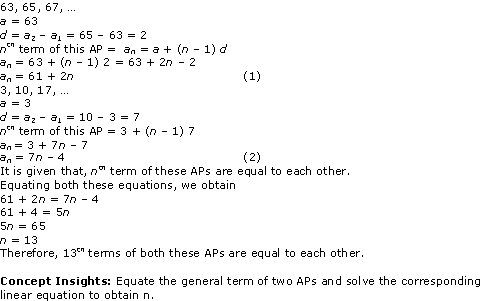
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 22

Question 16. Determine the A.P. whose third term is 16 and the 7^th term exceeds the 5^th term by 12.

Solution :
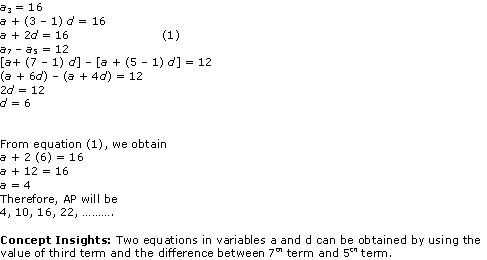
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 23

Page No: 107

Question 17. Find the 20^th term from the last term of the A.P. 3, 8, 13, …, 253.

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 24

Question 18. The sum of 4^th and 8^th terms of an A.P. is 24 and the sum of the 6^th and 10^th terms is 44. Find the first three terms of the A.P.

Solution :
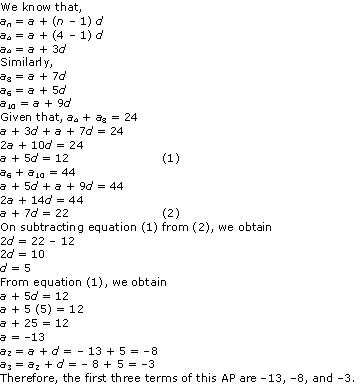
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 25

Question 19. Subba Rao started work in 1995 at an annual salary of Rs 5000 and received an increment of Rs 200 each year. In which year did his income reach Rs 7000?

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 26

Question 20. Ramkali saved Rs 5 in the first week of a year and then increased her weekly saving by Rs 1.75. If in the n^th week, her week, her weekly savings become Rs 20.75, find n.

Solution :
NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions 27

We hope the NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions Ex 5.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.4

November 27, 2020July 11, 2020 by Dattu

Get the comprehensive Chapter 14 Ex 14.4 Class 10 Maths NCERT Solutions from here and score good marks in CBSE Class 10 Board Examinations.

NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.4 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 14 Statistics Class 10 NCERT Solutions Ex 14.4.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 14
Chapter Name	Statistics
Exercise	Ex 14.4
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.4

NCERT Solutions for Class 10 Maths

Question 1.
The following distribution gives the daily income of 50 workers of a factory.

Daily income (in Rs)	100 – 120	120 – 140	140 – 160	160 – 180	180 – 200
Number of workers	12	14	8	6	10

Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.

Solution:

We can find frequency distribution table of less than type as following –

Daily income (in Rs)(upper class limits)	Cumulative frequency
Less than 120	12
Less than 140	12 + 14 = 26
Less than 160	26 + 8 = 34
Less than 180	34 + 6 = 40
Less than 200	40 + 10 = 50

Now taking upper class limits of class intervals on x-axis and their respective frequencies on y-axis we can draw its ogive as following –

NCERT Solutions for Class 10 Maths Chapter 14 Statistics Excercise 14.4 1s

Question 2.
During the medical check-up of 35 students of a class, their weights were recorded as follows:

Weight (in kg)	Number of students
Less than 38	0
Less than 40	3
Less than 42	5
Less than 44	9
Less than 46	14
Less than 48	28
Less than 50	32
Less than 52	35

Draw a less than type ogive for the given data. Hence obtain the median weight from the graph verify the result by using the formula.

Solution:
The given cumulative frequency distributions of less than type is –

Weight (in kg) upper class limits	Number of students (cumulative frequency)
Less than 38	0
Less than 40	3
Less than 42	5
Less than 44	9
Less than 46	14
Less than 48	28
Less than 50	32
Less than 52	35

Now taking upper class limits on x-axis and their respective cumulative frequency on y-axis we may draw its ogive as following

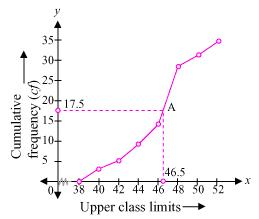
NCERT Solutions for Class 10 Maths Chapter 14 Statistics Excercise 14.4 2s

Now mark the point A whose ordinate is 17.5 its x-coordinate is 46.5. So median of this data is 46.5.
We may observe that difference between two consecutive upper class limits is 2. Now we may obtain class marks with their respective frequencies as below

Weight (in kg)	Frequency (f)	Cumulative frequency
Less than 38	0	0
38 – 40	3 – 0 = 3	3
40 – 42	5 – 3 = 2	5
42 – 44	9 – 5 = 4	9
44 – 46	14 – 9 = 5	14
46 – 48	28 – 14 = 14	28
48 – 50	32 – 28 = 4	32
50 – 52	35 – 32 = 3	35
Total (n)	35

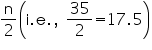Now the cumulative frequency just greater than NCERT Solutions for Class 10 Maths Chapter 14 Statistics Excercise 14.4 2s1 is 28 belonging to class interval 46 – 48
Median class = 46 – 48
Lower class limit (l) of median class = 46
Frequency (f) of median class = 14
Cumulative frequency (cf) of class preceding median class = 14
Class size (h) = 2
NCERT Solutions for Class 10 Maths Chapter 14 Statistics Excercise 14.4 2s2
So median of this data is 46.5
Hence, value of median is verified.

Question 3.
The following table gives production yield per hectare of wheat of 100 farms of a village.

Production yield (in kg/ha)	50 – 55	55 – 60	60 – 65	65 – 70	70 – 75	75 – 80
Number of farms	2	8	12	24	38	16

Change the distribution to a more than type distribution and draw ogive.

Solution:
We can obtain cumulative frequency distribution of more than type as following –

Production yield (lower class limits)	Cumulative frequency
more than or equal to 50	100
more than or equal to 55	100 – 2 = 98
more than or equal to 60	98 – 8 = 90
more than or equal to 65	90 – 12 = 78
more than or equal to 70	78 – 24 = 54
more than or equal to 75	54 – 38 = 16

Now taking lower class limits on x-axis and their respective cumulative frequencies on y-axis we can obtain its ogive as following.
NCERT Solutions for Class 10 Maths Chapter 14 Statistics Excercise 14.4 3s

We hope the NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.4 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.4

November 27, 2020July 11, 2020 by Dattu

NCERT Maths Solutions for Ex 1.4 Class 10 Real Numbers is the perfect guide to boost up your preparation during CBSE 10th Class Maths Examination.

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.4 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 1 Real Numbers Class 10 NCERT Solutions Ex 1.4.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 1
Chapter Name	Real Numbers
Exercise	Ex 1.4
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.4

Page No: 17

Question 1
Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i) 13/3125
(ii) 17/8
(iii) 64/455
(iv) 15/1600
(v) 29/343
(vi) 23/2³× 5²(vii) 129/2²× 5⁷× 7⁵(viii) 6/15
(ix) 35/50
(x) 77/210

Solution:

3125 = 5^₅
The denominator is of the form 5^m.
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers 17(i)
8 = 2³
The denominator is of the form 2^m.

455 = 5 x 7 x 13
Since the denominator is not in the form 2^_m x 5^_n, and it also contains 7 and 13 as its factors, its decimal expansion will be non-terminating repeating.

1600 = 2^₆ × 5^₂
The denominator is of the form 2^_m x 5^_n.

343 = 7^₃
Since the denominator is not in the form 2^_m x 5^_n, and it has 7 as its factor,
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers 23
The denominator is of the form 2^_m x 5^_n. Hence, the decimal expansion of is terminating.

(vii)
Since the denominator is not of the form 2^m 5ⁿ, and it also has 7 as its
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers 26
The denominator is of the form 5^_n.
10 = 2 x 5
The denominator is of the form 2^_m x 5^_n.

30 = 2 x 3 x 5
Since the denominator is not of the form 2^m × 5ⁿ, and it also has 3 as its factors,

Concept Insight: The concept used in this problem is that The decimal expansion of rational number p/q where p and q are coprime numbers, terminates if and only if the prime factorization of q is of the form 2ⁿ5^m, where n and m are non negative integers. Do not forget that 0 is also a non negative integer so n or m can take value 0.
Generally, mistake is committed in identifying terminating decimals when either of the two prime numbers 2 or 5 is appearing in the prime factorization.

Page No: 18

Question 2
Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.

Solution:

NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers 29

Concept Insight:
This is based on performing the long division and expressing the rational number in the decimal form learned in lower classes.

Question 3
The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form p, q you say about the prime factors of q?
(i) 43.123456789
(ii) 0.120120012000120000…
(iii) 43.123456789

Solution:
(i) 43.123456789
Since this number has a terminating decimal expansion, it is a rational number of the form p\q and q is of the form 2^m x 5ⁿ,
i.e., the prime factors of q will be either 2 or 5 or both.

(ii) 0.120120012000120000…
The decimal expansion is neither terminating nor recurring. Therefore, the given number is an irrational number.

(iii) 43.123456789
Since the decimal expansion is non-terminating recurring, the given number is a rational number of the form p/q and q is not of the form 2^_m x 5^_n i.e., the prime factors of q will also have a factor other than 2 or 5.

Concept Insight: The concept used in this problem is that, If the decimal expansion of rational number p\q, [where p and q are coprime numbers] terminates, then prime factorization of q is of the form 2ⁿ5^m, where n and m are non negative integers.

We hope the NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.4 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers Ex 1.4, drop a comment below and we will get back to you at the earliest.