NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.3 are part of NCERT Solutions for Class 10 Maths. Here are we have given Chapter 6 Triangles Class 10 NCERT Solutions Ex 6.3.
- Triangles Class 10 Ex 6.1
- Triangles Class 10 Ex 6.2
- Triangles Class 10 Ex 6.4
- Triangles Class 10 Ex 6.5
- Triangles Class 10 Ex 6.6
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 6 |
| Chapter Name | Triangles |
| Exercise | Ex 6.3 |
| Number of Questions Solved | 16 |
| Category | NCERT Solutions |
NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.3
NCERT Solutions for Class 10 Maths
Page No: 138
Question 1. State which pairs of triangles in Figure are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:
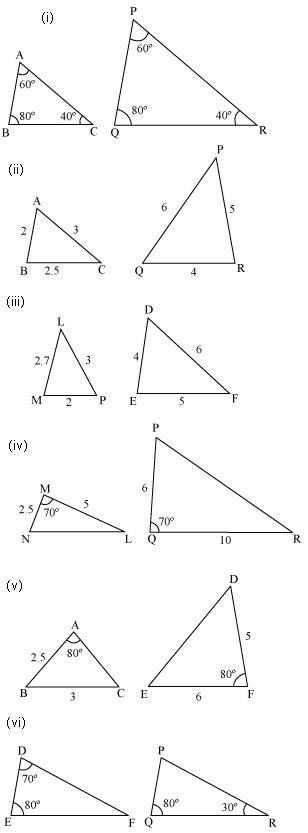
Solution:
(i) ∠A = ∠P = 600
∠B = ∠Q = 800
∠C = ∠R = 400
Therefore ∆ABC ~ ∆PQR [by AAA rule]

(iii) Triangles are not similar as the corresponding sides are not proportional.
(iv) Triangles are not similar as the corresponding sides are not proportional.
(v) Triangles are not similar as the corresponding sides are not proportional.
(vi) In ∆DEF
∠D + ∠E + ∠F = 1800
(Sum of measures of angles of a triangle is 1800)
700 + 800 + ∠F = 1800
∠F = 300
Similarly in ∠PQR
∠P + ∠Q + ∠R = 1800
(Sum of measures of angles of a triangle is 1800)
∠P + 800 +300 = 1800
∠P = 700
Now In ∆DEF and ∆PQR
∠D = ∠P = 700
∠E = ∠Q = 800
∠F = ∠R = 300
Therefore ∆DEF ~ ∆PQR [by AAA rule]
Page No: 139
Question 2. In the fig 6.35, ΔODC ∝ ¼ ΔOBA, ∠ BOC = 125° and ∠ CDO = 70°. Find ∠ DOC, ∠ DCO and ∠ OAB.
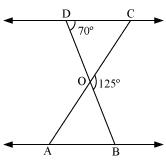
Solution:
Since DOB is a straight line
Therefore ∠DOC + ∠COB = 1800
Therefore ∠DOC = 1800 – 1250
= 550
In ∠DOC,
∠DCO + ∠CDO + ∠DOC = 1800
∠DCO + 700 + 550 = 1800
∠DCO = 550
Since ∆ODC ~ ∆OBA,
Therefore ∠OCD = ∠OAB [corresponding angles equal in similar triangles]
Therefore ∠ OAB = 550
Question 3. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that \(\frac { AO }{ OC } =\frac { OB }{ OD } \)
Solution:
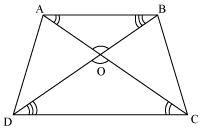
In ∆DOC and ∆BOA
AB || CD
Therefore ∠CDO = ∠ABO [Alternate interior angles]
∠DCO = ∠BAO [Alternate interior angles]
∠DOC = ∠BOA [Vertically opposite angles]
Therefore ∆DOC ~ ∆BOA [AAA rule)
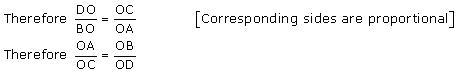
Page No: 140
Question 4. In the figure, QR/QS = QT/PR and ∠1 = ∠2. Show that ΔPQS ~ ΔTQR.
![]()
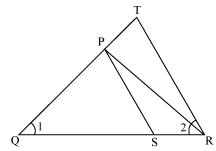
Solution:
In ∆PQR
∠PQR = ∠PRQ
Therefore PQ = PR (i)
Given,

Question 5. S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ~ ΔRTS.
Solution:
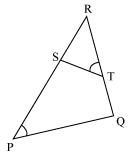
In ∆RPQ and ∆RST
∠RTS = ∠QPS [given]
∠R = ∠R [common angle]
∠RST = ∠RQP [ Remaining angles]
Therefore ∆RPQ ~ ∆RTS [by AAA rule]
Question 6. In the figure, if ΔABE ≅ ΔACD, show that ΔADE ~ ΔABC.
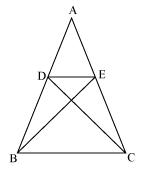
Solution:
Since ∆ABE ~ ∆ACD
Therefore
AB = AC ——(1)
AD = AE—— (2)
Now, in ∆ADE and ∆ABC,
Dividing equation (2) by (1)
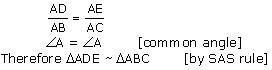
Question 7. In the figure, altitudes AD and CE of ΔABC intersect each other at the point P. Show that:
(i) ΔAEP ~ ΔCDP (ii) ΔABD ~ ΔCBE (iii) ΔAEP ~ ΔADB (iv) ΔPDC ~ ΔBEC
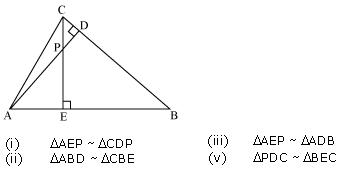
Solution:
(i)
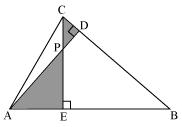
In ∆AEP and ∆CDP
Since ∠CDP = ∠AEP = 900
∠CPD = ∠APE (vertically opposite angles)
∠PCD = ∠PAE (remaining angle)
Therefore by AAA rule,
∆AEP ~ ∆CDP
(ii)
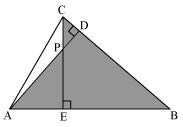
In ∆ABD and ∆CBE
∠ADB = ∠CEB = 900
∠ABD = ∠CBE (common angle)
∠DAB = ∠ECB (remaining angle)
Therefore by AAA rule
∆ABD ~ ∆CBE
(iii)
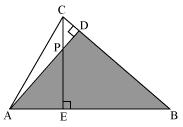
In ∆AEP and ∆ADB
∠AEP = ∠ADB = 900
∠PAE = ∠DAB (common angle)
∠APE = ∠ABD (remaining angle)
Therefore by AAA rule
∆AEP ~ ∆ADB
(iv)
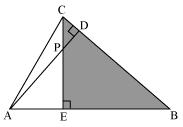
In ∆PDC and ∆BEC
∠PDC = ∠BEC = 900
∠PCD = ∠BCE (common angle)
∠CPD = ∠CBE
Therefore by AAA rule
∆PDC ~ ∆BEC
Question 8. E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE ~ ΔCFB.
Solution:
∆ABE and ∆CFB
∠A = ∠C (opposite angles of a parallelogram)
∠AEB = ∠CBF (Alternate interior angles AE || BC)
∠ABE = ∠CFB (remaining angle)
Therefore ∆ABE ~ ∆CFB (by AAA rule)
Question 9. In figure, ABC and AMP are two right triangles, right angled at B and M respectively, prove that:
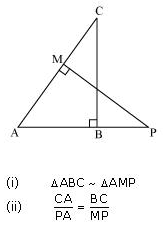
Solution:
In ∆ABC and ∆AMP
∠ABC = ∠AMP = 900
∠A = ∠A (common angle)
∠ACB = ∠APM (remaining angle)
Therefore ∆ABC ~ ∆AMP (by AAA rule)
Therefore \(\frac { CA }{ PA } =\frac { BC }{ MP } \) (Corresponding sides are proportional)
Question 10. CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively. If ΔABC ~ ΔFEG, Show that:
(i) CD/GH = AC/FG
(ii) ΔDCB ~ ΔHGE
(iii) ΔDCA ~ ΔHGF
Solution:
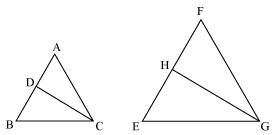
Since ∆ABC ~ ∆FEG
Therefore ∠A = ∠F
∠B = ∠E
As, ∠ACB = ∠FGE
Therefore ∠ACD = ∠FGH (angle bisector)
And ∠DCB = ∠HGE (angle bisector)
Therefore ∆ACD ~ ∆FGH (by AAA rule)
And ∆DCB ~ ∆HGE (by AAA rule)
For ∆ ACD and ∆FGH
\(\frac { CD }{ GH } =\frac { AC }{ FG } \)
Page No: 141
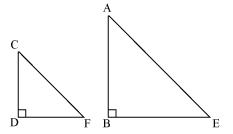
Question 11. In the following figure, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that ΔABD ~ ΔECF.
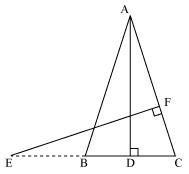
Solution:
In ∆ABD and ∆ECF,
Given that AB = AC (isosceles triangles)
So, ∠ABD = ∠ECF
∠ADB = ∠EFC = 900
∠BAD = ∠CEF
Therefore ∆ABD ~ ∆ECF (by AAA rule)
Question 12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR (see Fig 6.41). Show that ΔABC ~ ΔPQR.
Solution:
Median divides opposite side.
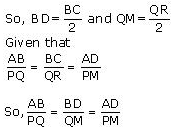
Therefore ∆ABD ~ ∆PQM (by SSS rule)
Therefore ∠ABD = ∠PQM (corresponding angles of similar triangles)
Therefore ∆ABC ~ ∆PQR (by SAS rule)
Question 13. D is a point on the side BC of a triangle ABC such that ∠ADC = ∠BAC. Show that CA2 = CB.CD
Solution:
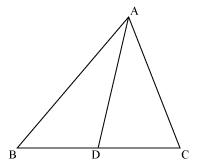
In ∆ADC and ∆BAC
Given that ∠ADC = ∠BAC
∠ACD = ∠BCA (common angle)
∠CAD = ∠CBA (remaining angle)
Hence, ∆ADC ~ ∆BAC [by AAA rule]
So, corresponding sides of similar triangles will be proportional to each other
\(\frac { CA }{ CB } =\frac { CD }{ CA } \)
Hence CA2 = CB × CD
Question 14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC ~ ΔPQR.
Solution:

Question 15. A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
Solution:
Let AB be a tower
CD be a pole
Shadow of AB is BE
Shadow of CD is DF
The light rays from sun will fall on tower and pole at same angle and at the same time.
So, ∠DCF = ∠BAE
And ∠DFC = ∠BEA
∠CDF = ∠ABE (tower and pole are vertical to ground)
Therefore ∆ABE ~ ∆CDF
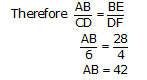
So, height of tower will be 42 meters.
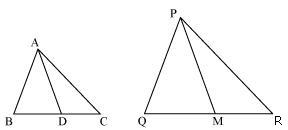
Question 16. If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR prove that AB/PQ = AD/PM.
Solution:

Since ∆ABC ~ ∆PQR
So, their respective sides will be in proportion
![]()
Also, ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R (2)
Since, AD and PM are medians so they will divide their opposite sides in equal halves.
![]()
From equation (1) and (3)

So, we had observed that two respective sides are in same proportion in both triangles and also angle included between them is respectively equal
Hence, ∆ABD ~ ∆PQM (by SAS rule)
![]()
We hope the NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.3 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex 6.3, drop a comment below and we will get back to you at the earliest.