What is Mean and What are its Advantages and Disadvantages
How to Find the Mean
If x1, x2, x3,…..,xn are n values of a variable X, then the arithmetic mean or simply the mean of these values is denoted by and is defined as
\(\overline X\) = \(\frac{{{x_1} + {x_2} + {x_3}…. + {x_n}}}{n}\) = \(\frac{1}{n}\left( {\sum\limits_{i = 1}^n {{x_i}} } \right)\)

Here the symbol \(\sum\limits_{i\, = \,1}^n {{x_i}}\) denotes the sum x1, x2, x3, ….., xn.
- If is the mean of n observations x1, x2, x3,…..,xn, then the mean of the observations x1 + a, x2 + a,…,xn + a is + a i.e. if each observation is increased by ‘a’, then the mean is also increased by ‘a’.
- If is the mean of x1, x2, x3,…..,xn then the mean of ax1, ax2,…axn is , where a is any number different from zero i.e. if each observation is multiplied by a non-zero number a, then the mean is also multiplied by ‘a’.
- If is the mean of n observations x1, x2, x3,…..,xn, then the mean of \(\frac { { x }_{ 1 } }{ a } ,\frac { { x }_{ 2 } }{ a } ,\frac { { x }_{ 3 } }{ a } ,….,\frac { { x }_{ 4 } }{ a } is\frac { \bar { X } }{ a } \), where a is any non-zero number.
- If is the mean of n observations x1, x2,…..,xn, then the mean of x1–a, x2 – a,…, xn – a is \(\overline X\) – a, where a is any real number.
Read More:
- How are Bar Graphs and Histograms Related
- Bar Graph in Statistics
- Median of Grouped Frequency Distribution
- Mode in Statistics
- Pie Charts
- Frequency Polygon
Arithmetic mean of raw data (when frequency is not given) :
The arithmetic mean of a raw data is obtained by adding all the values of the variables and dividing the sum by total number of values that are added.
Arithmetic mean \((\bar x) = \frac{{{x_1} + {x_2} + … + {x_n}}}{n} = \frac{1}{n}\sum\limits_{i\, = \,1}^n {{x_i}}\)
The symbol \(\sum\limits_{i\, = \,1}^n {{x_i}}\) denotes the sum x1 + x2 +…+ xn.
Advantages
- Arithmetic mean is simple to understand and easy to calculate.
- It is rigidly defined.
- It is suitable for further algebraic treatment.
- It is least affected fluctuation of sampling.
- It takes into account all the values in the series.
Disadvantages
- It is highly affected by the presence of a few abnormally high or abnormally low scores.
- In absence of a single item, its value becomes inaccurate.
- It can not be determined by inspection.
Mean Example Problems with Solutions
Example 1: If the mean of n observations ax1, ax2, ax3…axn is a, show that
\((a{x_1} – a\bar X)\) + \((a{x_2} – a\bar X)\) +…+ \((a{x_n} – a\bar X)\) = 0
Solution: We have
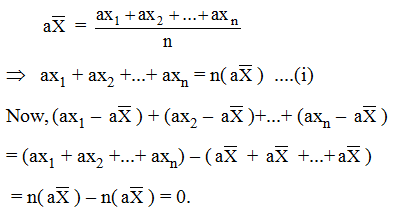
Example 2: The mean of 40 observations was 160. It was detected on rechecking that the value of 165 was wrongly copied as 125 for computation of mean. Find the correct mean.
Solution:

Example 3: The mean of 10 numbers is 20. If 5 is subtracted from every number, what will be the new mean?
Solution: Let x1, x2,…,x10 be 10 numbers with their mean equal to 20. Then,
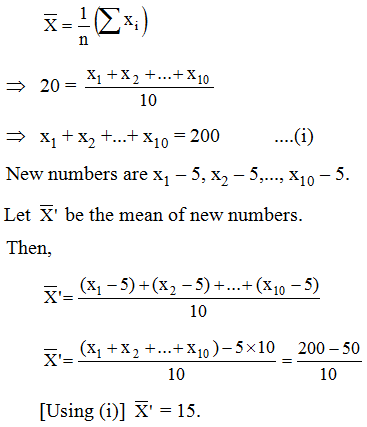
Example 4: Neeta and her four friends secured 65, 78, 82, 94 and 71 marks in a test of mathematics. Find the average (arithmetic mean) of their marks.
Solution: Arithmetic mean or average
= \(\frac{{65 + 78 + 82 + 94 + 71}}{5}\)
= \(\frac { 390 }{ 5 }\) = 78
Hence, arithmetic mean = 78
Example 5: The mean of 5, 7, p, 11, 15, 17, and 20 is 12, find p.
Solution: Mean = \(\frac{{5 + 7 + p + 11 + 15 + 17 + 20}}{7}\)
⇒ 12 = \(\frac{{75 + p}}{7}\)
⇒ p + 75 = 12 × 7
⇒ p = 9
Example 6: If the mean of 5 observations is 15 and that of another 10 observations is 20, find the mean of all 15 observations
Solution: Let first five observations be x1, x2, x3,…..,x5

Note :
If a variate X takes values x1, x2, x3,…..,xn with corresponding frequencies f1, f2, f3,…..,fn respectively, then arithmetic mean of these values is
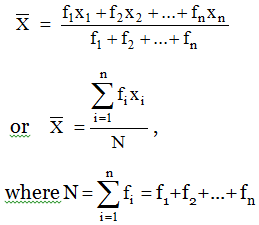
Example 7: Find the mean of the following distribution :
x : 4 6 9 10 15
f : 5 10 10 7 8
Solution: Calculation of Arithmetic Mean
| xi | fi | fixi |
| 4 | 5 | 20 |
| 6 | 10 | 60 |
| 9 | 10 | 90 |
| 10 | 7 | 70 |
| 15 | 8 | 120 |
| N = Σfi = 40 | Σfixi = 360 |
∴ Mean = \(\bar X = \frac{{\Sigma {f_i}{x_i}}}{{\Sigma {f_i}}} = \frac{{360}}{{40}}\) = 9.
Example 8: Find the mean of the following distribution :
x | 10 | 30 | 50 | 70 | 89 |
| f | 7 | 8 | 10 | 15 | 10 |
Solution: Calculation of Mean
| xi | fi | fixi |
| 10 | 7 | 70 |
| 30 | 8 | 240 |
| 50 | 10 | 500 |
| 70 | 15 | 1050 |
| 89 | 10 | 890 |
| N = Σfi = 50 | Σfixi = 2750 |
∴ Mean = \(\bar X = \frac{{\Sigma {f_i}{x_i}}}{{\Sigma {f_i}}} = \frac{{2750}}{{50}}\) = 55.
Example 9: Find the value of p, if the mean of following distribution is 7.5.
x | 3 | 5 | 7 | 9 | 11 | 13 |
| y | 6 | 8 | 15 | P | 8 | 4 |
Solution:
| xi | fi | fixi |
| 3 | 6 | 18 |
| 5 | 8 | 40 |
| 7 | 15 | 105 |
| 9 | p | 9p |
| 11 | 8 | 88 |
| 13 | 4 | 52 |
| N = Σfi = 41 + p | Σfixi = 303 + 9p |
We have, Σfi = 41 + p, Σfixi = 303 + 9p
∴ Mean = \(\frac{{\Sigma {f_i}{x_i}}}{{\Sigma {f_i}}}\) ⇒ 7.5 = \(\frac{{303 + 9p}}{{41 + p}}\)
⇒ 7.5 × (41 + p) = 303 + 9p
⇒ 307.5 + 7.5p = 303 + 9p
⇒ 9p – 7.5p = 307.5 – 303
⇒ 1.5p = 4.5
⇒ p = 3
Example 10: Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46.
Number of accidents (x) | 0 | 1 | 2 | 3 | 4 | 5 | Total |
| Frequency (f) | 46 | ? | ? | 25 | 10 | 5 | 200 |
Solution: Let the missing frequencies be f1 and f2
| xi | fi | fixi |
| 0 | 46 | 0 |
| 1 | f1 | f1 |
| 2 | f2 | 75 |
| 3 | 25 | 2f2 |
| 4 | 10 | 40 |
| 5 | 5 | 25 |
| N = 86 + f1 + f2 | Σfixi = 140 + f1 + 2f2 |
We have N = 200
∴ 200 = 86 + f1 + f2 ⇒ f1 + f2 = 114 ….(i)
Also,
Mean = 1.46
⇒ 1.46 = \(\frac{{\Sigma {f_i}{x_i}}}{N}\) ⇒ 1.46 = \(\frac{{140 + {f_2} + 2{f_2}}}{{200}}\)
⇒ 292 = 140 + f1 + 2f2
⇒ f1 + 2f2 = 152 ….(ii)
Solving (i) and (ii) we get f1 = 76 and f2 = 38.
Example 11: If the mean of the following data be 9.2, find the value of p.
| x | 4 | 6 | 7 | p + 4 | 12 | 12 |
| f | 5 | 6 | 4 | 10 | 8 | 7 |
Solution:
| x | f | f×x |
| 4 | 5 | 20 |
| 6 | 6 | 36 |
| 7 | 4 | 28 |
| p+4 | 10 | 10p + 40 |
| 12 | 8 | 96 |
| 14 | 7 | 98 |
| Total | 40 | 318 + 10p |
Now,
Mean = \(\bar x = \frac{{\Sigma f\, \times x}}{{\Sigma f}}\) = \(\frac{{318 + 10 \times p}}{{40}}\)
∴ 9.2 = \(\frac{{318 + 10 \times p}}{{40}}\)
⇒ 318 + 10.p = 368 ⇒ 10p = 50 ⇒ p = 5
Example 12: The marks of 30 students are given below, find the mean marks.
| Marks | Number of Students |
| 10 | 4 |
| 11 | 3 |
| 12 | 8 |
| 13 | 6 |
| 14 | 7 |
| 15 | 2 |
Solution:
| x | f | f×x |
| 10 | 4 | 40 |
| 11 | 3 | 33 |
| 12 | 8 | 96 |
| 13 | 6 | 78 |
| 14 | 7 | 98 |
| 15 | 2 | 30 |
| Σf = 30 | Σfx = 375 |
Mean = \(\frac{{\Sigma fx}}{{\Sigma f}}\) = \(\frac { 375 }{ 30 } \)
= 12.5
Example 13: The mean of n observations x1, x2,…,xn is \(\bar { X } \). If (a – b) is added to each of the observations, show that the mean of the new set of observations is \(\bar { X } \) + (a – b).
Solution: We have,
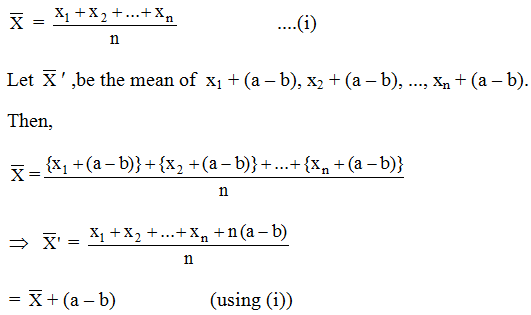
Example 14: Find the sum of the deviations of the variate values 3, 4, 6, 8, 14 from their mean.
Solution: Recall that the deviations of the values x1, x2, x3, …, xn about A are x1 – A, x2 – A, x3 – A,…, xn – A.
Let \(\bar { X } \) be the mean of the values 3, 4, 6, 8, 14. Then,
\(\bar { X } \) = \(\frac{{3 + 4 + 6 + 8 + 14}}{5} = \frac{{35}}{5}\) = 7
Now, sum of the deviations of the values 3, 4, 6, 8, 14 from their mean = 7 is given by
= (3 – 7) + (4 – 7) + (6 – 7) + (8 – 7) + (14 – 7) = – 4 – 3 – 1 + 1+ 7 = 0.
Example 15: The mean of 16 numbers is 8. If 2 is added to every number, what will be the new mean ?
Solution: Let x1,x2,x3,…,x16 be 16 numbers with their mean equal to 8. Then,
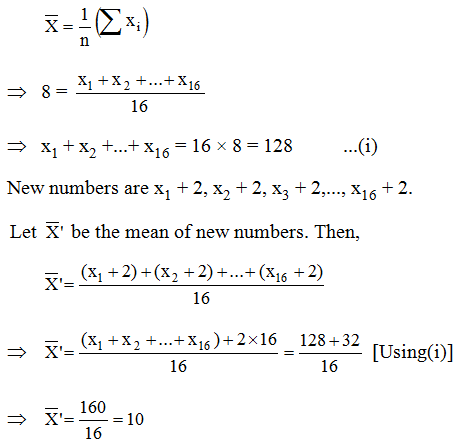
Example 16: If x1, x2,…,xn are n values of a variable X such that
\(\sum\limits_{i\, = \,1}^n {({x_i} – 2)}\) = 110 and \(\sum\limits_{i\, = \,1}^n {({x_i} – 5)}\) = 20.
Find the value of n and the mean.
Solution: We have,
\(\sum\limits_{i\, = \,1}^n {({x_i} – 2)}\) = 110 and \(\sum\limits_{i\, = \,1}^n {({x_i} – 5)}\) = 20
⇒ (x1 – 2) + (x2 – 2) +…+ (xn – 2) = 110
and (x1 – 5) + (x2 – 5) +…+ (xn – 5) = 20
⇒ (x1 + x2 +…+ xn) – 2n = 110 and (x1 + x2 +…+ xn) –5n = 20
⇒ \(\sum\limits_{i\,\, = \,\,1}^n {{x_i}} – 2n\) = 110 and \(\sum\limits_{i\,\, = \,\,1}^n {{x_i}} – 5n\) = 20
⇒ S – 2n = 110 and S – 5n = 20
Thus, we have
S – 2n = 110 ….(i)
and S – 5n = 20 ….(ii)
Subtracting (ii) from (i), we get
3n = 90 ⇒ n = 30
Putting n = 30 in (i), we get
S – 60 = 110 ⇒ S = 170
⇒ \(\sum\limits_{i\,\, = \,\,1}^n {{x_i} = 170}\)
∴ Mean = \(\frac{1}{n}\left( {\sum\limits_{i\,\, = \,\,1}^n {{x_i}} } \right) = \frac{{170}}{{30}} = \frac{{17}}{3}\)
Hence, n = 30 and mean .
Example 17: The sum of the deviations of a set of n values x1,x2,…,xn measured from 50 is–10 and the sum of deviations of the values from 46 is 70. Find the values of n and the mean.
Solution: We have,
\(\sum\limits_{i\,\, = \,\,1}^n {({x_i} – 50) = – 10}\) and \(\sum\limits_{i\,\, = \,\,1}^n {({x_i} – 46) = 17}\)
⇒ \(\sum\limits_{i\,\, = \,\,1}^n {{x_i} – 50n = – 10}\) ….(i)
and \(\sum\limits_{i\,\, = \,\,1}^n {{x_i} – 46n = 70}\) ….(ii)
Subtracting (ii) from (i), we get
–4n = – 80 ⇒ n = 20
Putting n = 20 in (i), we get
\(\sum\limits_{i\,\, = \,\,1}^n {{x_i} = 50 \times 20}\) = –10 ⇒ \(\sum\limits_{i\,\, = \,\,1}^n {{x_i} = 990}\)
∴ Mean = \(\frac{1}{n}\left( {\sum\limits_{i\, = \,\,1}^n {{x_i}} } \right) = \frac{{990}}{{20}} = 49.5\)
Hence, n = 20 and mean = 49.5
Example 18: The marks obtained by 10 students in physics out of 40 are 24, 27, 29, 34, 32, 19, 26, 35, 18, 21. Compute the mean of the marks.
Solution: Mean of the marks is given by
\(\bar x = \frac{{24 + 27 + 29 + 34 + 32 + 19 + 26 + 35 + 18 + 21}}{{10}}\)
= \(\frac{265}{10}\) = 26.50
Example 19: The mean of 20 observations was found to be 47. But later it was discovered that one observation 66 was wrongly taken as 86. Find the correct mean.
Solution: Here, n = 20, = 47
We have, \({\rm{\bar x}} = \frac{{\sum\limits_{{\rm{i}} = {\rm{1}}}^{\rm{n}} {{{\rm{x}}_{\rm{i}}}} }}{n}\)
∴ 47 = \(\frac{{\sum\limits_{{\rm{i}} = {\rm{1}}}^{\rm{n}} {{{\rm{x}}_{\rm{i}}}} }}{{20}}\)
\(\sum\limits_{{\rm{i}} = {\rm{1}}}^{\rm{n}} {{{\rm{x}}_{\rm{i}}}}\) = 47 × 20 = 940.
But the score 66 was wrongly taken as 86.
∴ Correct value of \(\sum\limits_{{\rm{i}} = {\rm{1}}}^{\rm{n}} {{{\rm{x}}_{\rm{i}}}}\) = 940 + 66 – 86 = 920
∴ Correct mean = = 46
Example 20: If denote the mean of x1, x2, …, xn, show that
\(\sum\limits_{i = 1}^n { = ({x_i} – \bar x)}\)
Solution: \(\bar x = \frac{{{x_1} + {x_2} + … + {x_n}}}{n}\)
= x1 + x2 +… + xn = n\(\bar x\) (i)
= S(x1 – \(\bar x\) ) = (x1 – \(\bar x\)) + (x2 – \(\bar x\)) +….. + (xn – x1)
= (x1 + x2+ … + xn) – n\(\bar x\) = n\(\bar x\) – n\(\bar x\)
= 0 (from (i))
Example 21: If the heights of 5 persons are 144 cm, 153 cm, 150 cm, 158 cm and 155 cm respectively, then find the mean height.
Solution: Mean Height = \(\frac{{144 + 153 + 150 + 158 + 155}}{5}\)
= \(\frac{760}{5}\) = 152 cm.
Example 22: Find the arithmetic mean of the following frequency distribution :
x : 4 7 10 13 16 19
f : 7 10 15 20 25 30
Solution: The given frequency distribution is –
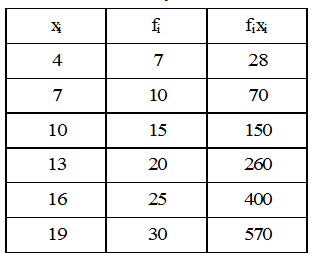
Σfi = 107
Σfixi = 1478
\(\bar x\) = \(\frac{{\sum {{f_i}\,\,{x_i}} }}{{\sum {{f_i}} }}\) = \(\frac{{1478}}{{107}}\) = 13.81
Example 23: The mean income of a group of persons is Rs.400. Another group of persons has mean income Rs.480. If the mean income of all the persons in the two groups together is Rs.430, then find the ratio of the number of persons in the groups.
Solution: \(\bar x\) = \(\frac{{{n_1}{{\bar x}_1} + {n_2}{{\bar x}_2}}}{{{n_1} + {n_2}}}\)
\({\bar x_1}\) = 400, \({\bar x_2}\) = 480, \({\bar x_3}\) = 430
∴ 430 = \(\frac{{{n_1}(400) + \,{n_2}(480)}}{{{n_1} + {n_2}}}\)
⇒ 30n1 = 50n2
⇒ \(\frac{{{n_1}}}{{{n_2}}} = \frac{5}{3}\)
Example 24: Mean of 25 observations was found to be 78.4. But later on it was found that 96 was misread 69. Find the correct mean.
Solution: Mean \(\bar x\) = \(\frac{{\sum x }}{n}\)
or Σx = n
Σx = 25 × 78.4 = 1960
But this Σx is incorrect as 96 was misread as 69.
∴ correct Σx = 1960 + (96 – 69) = 1987
∴ correct mean = = 79.47