Math Labs with Activity – Verify that the Quadrilateral Formed by Joining the Midpoints

Math Labs with Activity – Verify that the Quadrilateral Formed by Joining the Midpoints

OBJECTIVE

To verify that the quadrilateral formed by joining the midpoints of the sides of a quadrilateral is a parallelogram

Materials Required

1. A sheet of white paper
2. A sheet of glazed paper
3. A geometry box
4. A pair of scissors

Procedure
Step 1: Draw any quadrilateral ABCD on the white paper. Fold the paper so that point A falls on the point B. Make a crease and unfold the paper. Mark the point P where the line of fold cuts the side AB. Then, P is the midpoint of side AB of the quadrilateral. Similarly, find the midpoints Q, R and S of the sides BC, CD and DA respectively.
Step 2: Join the points P, Q, R and S to form the quadrilateral PQRS as shown in Figure 23.1.

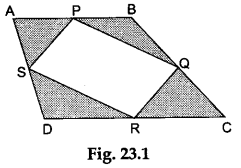
Step 3: Make an exact copy of the quadrilateral PQRS on the glazed paper. Draw a diagonal by joining the points S and Q as shown in Figure 23.2.

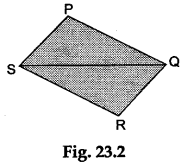
Step 4: Cut ΔPQS. Rotate and place it over the ΔSQR as shown in Figure 23.3.

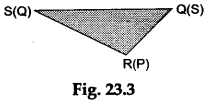
Observations
ΔPQS exactly covers ΔSQR.
Therefore, ΔPQS is congruent to ΔSQR and so, PQ = SR and PS = QR, i. e., two pairs of opposite sides are equal.
Hence, PQRS is a parallelogram.

Result
The quadrilateral formed by joining the midpoints of the sides of a quadrilateral is a parallelogram.

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills