Math Labs with Activity – Verify the Properties of a Trapezium

by

Math Labs with Activity – Verify the Properties of a Trapezium

OBJECTIVE

To verify the properties of a trapezium

Materials Required

  1. Two sheets of white paper
  2. A geometry box
  3. A pair of scissors
  4. A tube of glue

Theory
By geometry, we know that in a trapezium ABCD, if AB || DC and E and F are the midpoints of the sides AD and BC respectively then

  1. EE || AB, and
  2. EF = ½(AB+DC).

Procedure
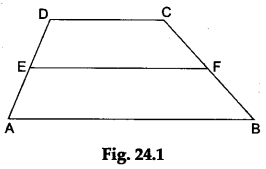
Step 1: Construct a trapezium ABCD (in which AB || DC)
on a sheet of white paper. Mark the midpoints E and F of the non-parallel sides AD and BC respectively (the midpoints of the sides can be obtained by the method of paper folding). Join EE (see Figure 24.1).
Math Labs with Activity - Verify the Properties of a Trapezium 1
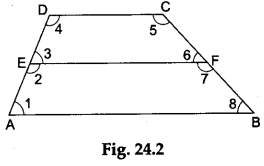
Step 2: Mark the angles in the diagram as shown in Figure 24.2.
Math Labs with Activity - Verify the Properties of a Trapezium 2
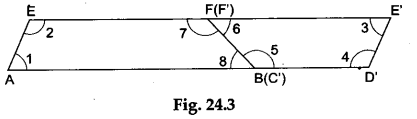
Step 3: Paste the two quadrilaterals ABFE and EFCD as shown in Figure 24.3.
Math Labs with Activity - Verify the Properties of a Trapezium 3

Observations and Calculations

  1. In Figure 24.2, for the trapezium ABCD we have AB || DC.
    ∴ ∠5 + ∠8 = 180° (consecutive interior angles) and so, in Figure 24.3, ∠5 and ∠8 form a linear pair, i.e., AD’ is a straight line.
    Also, in Figure 24.2 we have ∠6 + ∠7 = 180° (since ∠6 and ∠7 form a linear pair) and so, in Figure 24.3, ∠6 and ∠7 form a linear pair, i.e., EE’ is a straight line.
    Hence, AD’E’E is a quadrilateral.
  2. In Figure 24.2, for the trapezium ABCD we have AB || DC.
    ∠1 + ∠4 = 180° (consecutive interior angles) and so, in Figure 24.3, AE || E’D’ (since ∠1 and ∠4 are consecutive interior angles).
  3. In Figure 24.2, we have AE = ED (∴ E is the midpoint of AD) in Figure 24.3, we have AE=E’D’ (since E’D’=ED).
    Thus, we have AE || E’D’ and AE =E’D’.
    Hence, the quadrilateral AD’E’E is a parallelogram (a pair of opposite sides being equal and parallel).
  4. AD’E’E being a parallelogram, we have
    (i) EE’ || AD’ and (ii) EE’ = AD’.
    Now, EE’ || AD’ => EF || AB (see Figure 24.3)
    and EE’=AD’ => EF+E’F’ =AB+C’D’ => 2EF=AB+CD
    (∴ E’F’=EF and C’D’=CD) => EF = ½(AB+DC).

Result
It is verified that in a trapezium ABCD, if AB || DC, E is the midpoint of side AD and F is the midpoint of side BC then

  1. EF || AB
  2. EF = ½ (AB+DC)

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills

Leave a Comment