Math Labs with Activity – Verify the Midpoint Theorem

Math Labs with Activity – Verify the Midpoint Theorem

OBJECTIVE

To verify the midpoint theorem.

Materials Required

1. A piece of cardboard
2. Two sheets of white paper
3. A geometry box
4. A black marker pen

Theory
Midpoint theorem: The line segment joining the midpoints of any two sides of a triangle is parallel to the third side.

Procedure
Step 1: Paste one sheet of white paper on the cardboard.
Draw a ΔABC on this paper.
Step 2: Mark the midpoints D and E of the sides AB and AC respectively (the midpoints of the sides can be obtained by the method of paper folding). Join D and E. Blacken ΔADE with the marker pen.
Step 3: Cut another triangle CEE from the other sheet of white paper so that ΔCEE is congruent to ΔADR Blacken ΔCEE with the marker pen. Place ΔCEF on the previous paper as shown in Figure 22.1.

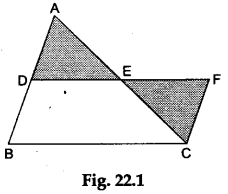
Observations

1. 1. Since ΔCEF is congruent to ΔADE, therefore DE = £F.
   2. Measure DE and BC. We find that DE = ½ BC.
   3. From (i) and (ii), we derive that DF = BC.
2. 1. Since ΔCEF is congruent to ΔADE, therefore AD = FC.
   2. Since D is the midpoint of AB, we have AD = DB.
   3. From (i) and (ii), we get FC = DB.
3. From the above observations, it is clear that DFCB is a parallelogram.
   Hence, DE || BC.

Result
The midpoint theorem is verified.

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills