Find The HCF And LCM using Prime Factorisation Method
Relation between two numbers and their HCF and LCM
Consider two numbers 18 and 24.
Prime factorisation of 18 = 2 × 3 × 3
Prime factorisation of 24 = 2 × 2 × 2 × 3
So, HCF = 2 × 3 = 6
LCM = 2 × 2 × 2 × 3 × 3 = 72
Product of HCF and LCM = 6 × 72 = 432
Product of given numbers = 18 × 24 = 432
The product of LCM and HCF of two natural numbers is equal to the product of the given natural numbers.
∴ Product of given numbers = HCF × LCM of given numbers
For any two positive integers:
Their LCM. × their HCF. = Product of the number
(i) LCM = \(\frac{\text{Product of the numbers}}{\text{HCF}}\)
(ii) HCF = \(\frac{\text{Product of the numbers}}{\text{LCM}}\)
(iii) One number = \(\frac{\text{H}\text{.C}\text{.F}\text{. }\!\!\times\!\!\text{ L}\text{.C}\text{.M}\text{.}}{\text{Other number}}\)
Finding HCF And LCM using Prime Factorisation Method Example Problems With Solutions
Find the L.C.M. and H.C.F. of the following pairs of integers by applying the Fundamental theorem of Arithmetic method i.e., using the prime factorisation method.
Example 1: 26 and 91
Sol. Since, 26 = 2 × 13 and, 91 = 7 × 13

L.C.M. = Product of each prime factor with highest powers. = 2 × 13 × 7 = 182.
i.e., L.C.M. (26, 91) = 182.
H.C.F. = Product of common prime factors with lowest powers. = 13.
i.e., H.C.F (26, 91) = 13.
Product of given two numbers = 26 × 91 = 2366
and, product of their L.C.M. and H.C.F. = 182 × 13 = 2366
Product of L.C.M and H.C.F of two given numbers = Product of the given numbers
Example 2: 1296 and 2520
Sol. Since, 1296 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3 = 24 × 34
and, 2520 = 2 × 2 × 2 × 3 × 3 × 5 × 7 = 23 × 32 × 5 × 7

L.C.M. = Product of each prime factor with highest powers
= 24 × 34 × 5 × 7 = 45,360
i.e., L.C.M. (1296, 2520) = 45,360
H.C.F. = Product of common prime factors with lowest powers = 23 × 32 = 8 × 9 = 72
i.e., H.C.F. (1296, 2520) = 72.
Product of given two numbers = 1296 × 2520 = 3265920
and, product of their L.C.M. and H.C.F. = 45360 × 72 = 3265920
L.C.M. (1296, 2520) × H.C.F. (1296, 2520)
= 1296 × 2520 = 3265920
Example 3: 17 and 25
Sol. Since, 17 = 17
and, 25 = 5 × 5 = 52
L.C.M. = 17 × 52 = 17 × 25 = 425
and, H.C.F. = Product of common prime factors with lowest powers = 1, as given numbers do not have any common prime factor.
The given numbers 17 and 25 do not have any common prime factor. Such numbers are called co-prime numbers and their H.C.F. is always equal to 1 (one), whereas their L.C.M. is equal to the product of the numbers.
But in case of two co-prime numbers also, the product of the numbers is always equal to the product of their L.C.M. and their H.C.F.
As, in case of co-prime numbers 17 and 25;
H.C.F. = 1; L.C.M. = 17 × 25 = 425;
product of numbers = 17 × 25 = 425
and product of their H.C.F. and L.C.M. = 1 × 425 = 425.
Example 4: Given that H.C.F. (306, 657) = 9, find L.C.M. (306, 657)
Sol. H.C.F. (306, 657) = 9 means H.C.F. of
306 and 657 = 9
Required L.C.M. (306, 657) means required L.C.M. of 306 and 657.
For any two positive integers;
their L.C.M. = \(\frac{\text{Product of the numbers}}{\text{H}\text{.C}\text{.F}\text{.}}\)
i.e., L.C.M. (306, 657) = \(\frac{306\times 657}{9}\) = 22,338.
Example 5: Given that L.C.M. (150, 100) = 300, find H.C.F. (150, 100)
Sol. L.C.M. (150, 100) = 300
⇒ L.C.M. of 150 and 100 = 300
Since, the product of number 150 and 100
= 150 × 100
And, we know :
H.C.F. (150, 100) = \(\frac{\text{Product of 150 and 100}}{L.C.M\text{.(150,100)}}\)
= \(\frac{150\times 100}{300}\) = 50.
Example 6: The H.C.F. and L.C.M. of two numbers are 12 and 240 respectively. If one of these numbers is 48; find the other numbers.
Sol. Since, the product of two numbers
= Their H.C.F. × Their L.C.M.
⇒ One no. × other no. = H.C.F. × L.C.M.
⇒ Other no. = \(\frac{12\times 240}{48}\) = 60.
Example 7: Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 + 5 are composite numbers.
Sol. Since,
7 × 11 × 13 + 13 = 13 × (7 × 11 + 1)
= 13 × 78 = 13 × 13 × 3 × 2;
that is, the given number has more than two factors and it is a composite number.
Similarly, 7 × 6 × 5 × 4 × 3 + 5
= 5 × (7 × 6 × 4 × 3 + 1)
= 5 × 505 = 5 × 5 × 101
∴ The given no. is a composite number.
Maths

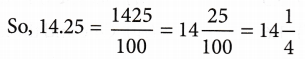

 Example 3: Convert the following into decimals.
Example 3: Convert the following into decimals.