What is a Decimal Value and Place Value of Decimals
Decimal Fractions
Introduction
Riya, Nutan, and Roshan are studying in the same class. In the mathematics examination, marks obtained by Riya and Nutan are 72 and 78 respectively, but the marks obtained by Roshan is 80.5.

Children, do you know the meaning of 80.5 ? It is nothing but \(80\frac{1}{2}\). \(\frac{1}{2}\) can also be written as 0.5.
0. 5 is the decimal representation of fraction \(\frac{1}{2}\). A decimal number is a number that contains a decimal point.
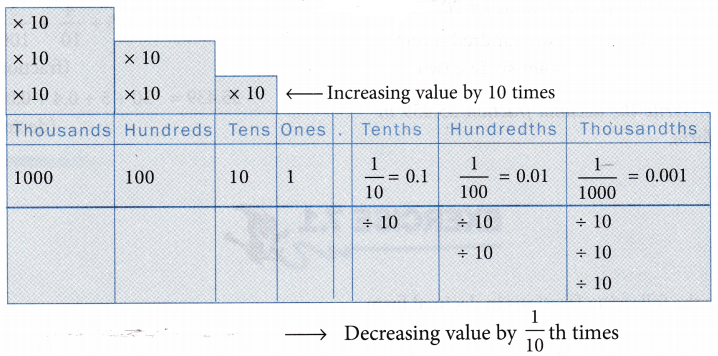
We know that the place value of a digit increases 10 times as it moves one step towards the left or decreases \(\frac{1}{10}\) times as it moves one step towards the right. Watch the place value of digits in the Table.
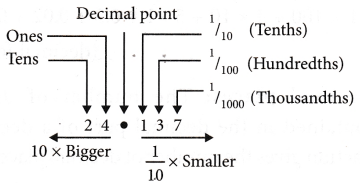
Decimal Fractions
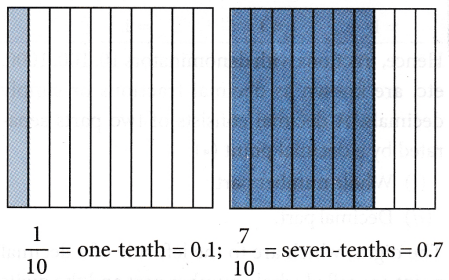
Let us consider a square divided into ten equal parts, then each part of the square will represent one-tenth \((\frac{1}{10})\) of the whole square. The decimal form of one-tenth is 0.1 read as ‘zero decimal one’ or ‘zero point one’; The fractional form of one tenth is \((\frac{1}{10})\)
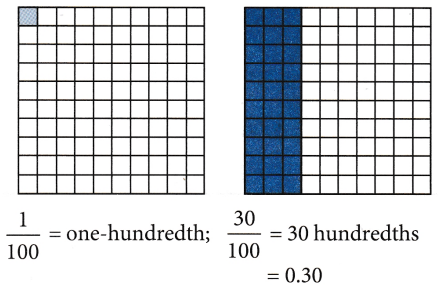
When we divide a square into 100 equal parts, then each part of square represents \((\frac{1}{100})\), which is called
‘one hundredth’ and can be written in the decimal form as 0.01.
Note: The word ‘DECIMAL’ means ‘based on 10’. This word is derived from the latin word decima meaning – a tenth part.
Similarly, if we divide a square into 1000 equal parts, then each part will be represented by \((\frac{1}{1000})\) called ‘one-thousandth’ and written as 0.001 in decimal form.
From the above, it is clear that

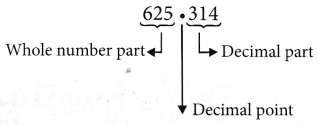
Hence, fractions with denominators 10,100,1000, etc. are known as decimal fractions or simply decimals. A decimal consists of two parts separated by a decimal point (•)
(i) Whole number part
(ii) Decimal part.
The digits, which are to the left side of a decimal point are called whole number part and the digits which are to the right side of a decimal point are called decimal part.
Example
Reading of a decimal fraction
While reading a decimal fraction, the digits on the left of the decimal point are read as whole number and the digits on the right of the decimal point are read as individual digits.
Example: 625.314 can be read as six hundred twenty-five point three one four.
22.768 = twenty-two point seven six eight.
Observe the following:
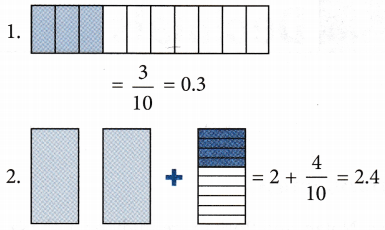
Note:
If there is no whole number part in a decimal number then write 0 on the left of the decimal point.
Example: 0.67, 0.132, 0.5, etc
Writing decimals in place value chart
Table given on the next page shows the value of each place in a decimal fraction.
We can use this place value chart to expand a decimal fraction using decimals or fractions.
Expanded Form
This is a form, in which we add the place value of each digit forming the number.
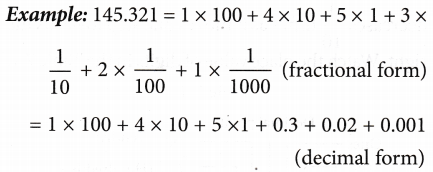
Decimal places: The number of digits contained in the decimal part of a decimal fraction gives the number of decimal places.
Read More About:
- What is the meaning of Place Value and Face Value in Maths?
- What is the Place Value Chart of an Indian and International System?
- How do you Round to the Nearest Ten Thousand
- What is the Definition of an Equivalent Decimal
- Converting To and From Scientific Notation
- What is the Difference between Ascending and Descending Order
- Addition and Subtraction of Decimals
- How do you Multiply and Divide Decimals?
- How do you Convert Fractions into Decimals and Vice Versa
- How do you Convert Unlike Decimals into Like Decimals