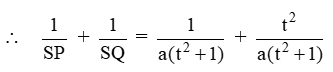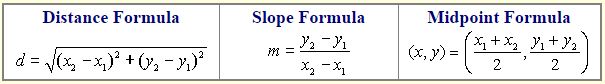ICSE Solutions for Class 10 Mathematics – Coordinate Geometry
ICSE SolutionsSelina ICSE Solutions
Get ICSE Solutions for Class 10 Mathematics Chapter 11 Coordinate Geometry for ICSE Board Examinations on APlusTopper.com. We provide step by step Solutions for ICSE Mathematics Class 10 Solutions Pdf. You can download the Class 10 Maths ICSE Textbook Solutions with Free PDF download option.
Download Formulae Handbook For ICSE Class 9 and 10
Formulae



Formulae Based Questions
Question 1. Find the distance of the following points from origin.
(i) (5, 6) (ii) (a+b, a-b) (iii) (a cos θ, a sin θ).

Question 2. Calculate the distance between A (7, 3) and B on the x-axis, whose abscissa is 11.
Solution: Here B is (11, 0)
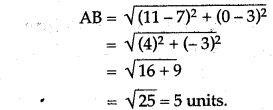
Question 3. KM is a straight line of 13 units If K has the coordinate (2, 5) and M has the coordinates (x, – 7) find the possible value of x.

Question 4. The midpoint of the line segment joining (2a, 4) and (-2, 2b) is (1, 2a+1). Find the value of a and b.
show that the points A(- 1, 2), B(2, 5) and C(- 5, – 2) are collinear.
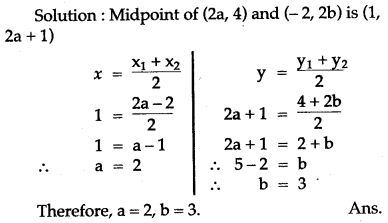
Question 5. Use distance formula to show that the points A(-1, 2), B(2, 5) and C(-5, -2) are collinear.

Determine the Following
Question 1. PQ is straight line of 13 units. If P has coordinate (2, 5) and Q has coordinate (x, – 7) find the possible values of x.
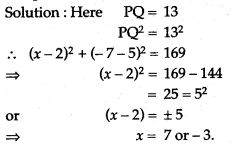
Question 2. Give the relation that must exist between x and y so that (x, y) is equidistant from (6, -1) and (2, 3).

Question 3. The line segment joining A (2, 3) and B (6, – 5) is intersected by the X axis at the point K. Write the ordinate of the point K. Hence find the ratio in which K divides AB.
Solution: A (2, 3) and B (6,- 5)

Question 4. Find the value of x so that the line passing through (3, 4) and (x, 5) makes an angle 135° with positive direction of X-axis.
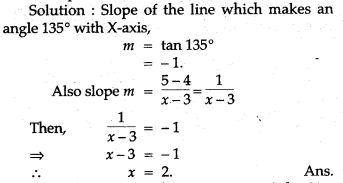
Question 5. Find the value, of k, if the line represented by kx – 5y + 4 = 0 and 4x – 2y + 5 = 0 are perpendicular to each other.

Question 6. Find the equation of a line which is inclined to x axis at an angle of 60° and its y – intercept = 2.
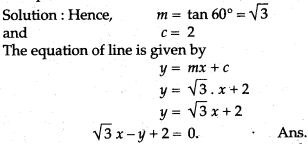
Question 7. Find the equation of a line with slope 1 and cutting off an intercept of 5 units on Y-axis.
Solution: We have
Slope of the line m = 1

Question 8. Find the equations of a line passing through the point (2, 3) and having the x – interecpt of 4 units.

Question 9. The line through A (- 2, 3) and B (4, b) is perpendicular to the line 2a – 4y = 5. Find the value of b.


Question 11. Find the equation of a straight line which cuts an intercept of 5 units on Y-axis and is parallel to the line joining the points (3, – 2) and (1, 4).

Question 12. Find the equation of a line that has Y-intercept 3 units and is perpendicular to the line joining (2, – 3) and (4, 2).

Question 13. Find a general equation of a line which passes through:
(i) (0, -5) and (3, 0) (ii) (2, 3) and (-1, 2).

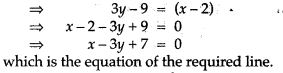
Question 14. Find the equation of the line passing through (0, 4) and parallel to the line 3x + 5y + 15 = 0.

Question 15. Find the equation of a line passing through (3, – 2) and perpendicular to the line.

Question 16. Find the equation of the straight line which has Y-intercept equal to 4/3 and is perpendicular to 3x – 4y + 11 = 0.
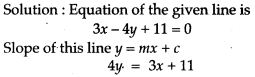

Question 17. Find the equation of the straight line perpendicular to 5x – 2y = 8 and which passes through the mid-point of the line segment joining (2, 3) and (4, 5).

Question 18. A line passing through the points (a, 2a) and (- 2, 3) is perpendicular to the line 4a + 3y + 5 = 0. Find the value of a.
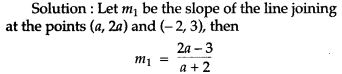

Prove the Following
Question 1. A line is of length 10 units and one end is at the point (2, – 3). If the abscissa of the other end be 10, prove that its ordinate must be 3 or – 9.

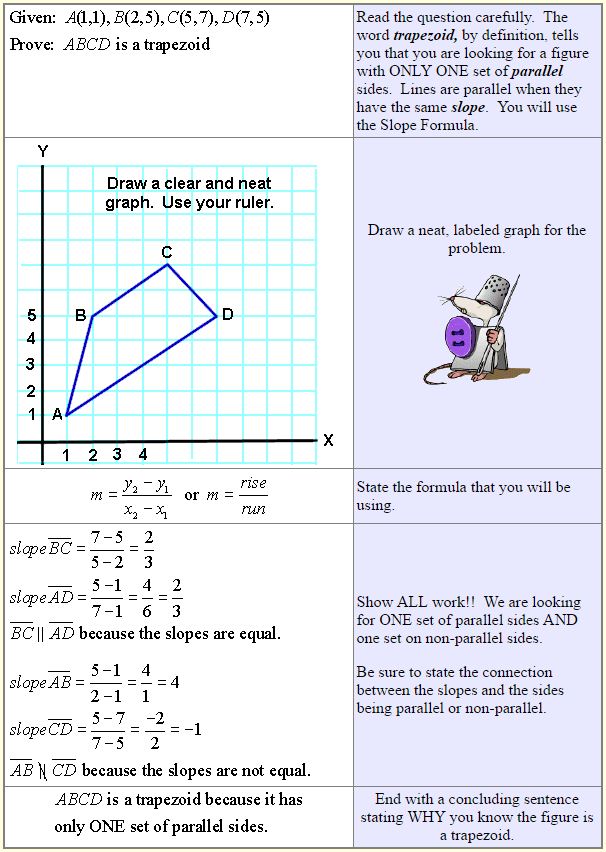
Question 2. Show that the line joining (2, – 3) and (- 5, 1) is:
(i) Parallel to line joining (7, -1) and (0, 3).
(ii) Perpendicular to the line joining (4, 5) and (0, -2).

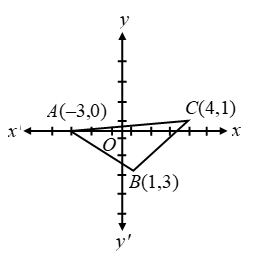
Question 3. With out Pythagoras theorem, show that A(4, 4), B(3, 5) and C(-1, -1) are the vertices of a right angled.

Question 4. Show that the points A(- 2, 5), B(2, – 3) and C(0, 1) are collinear.
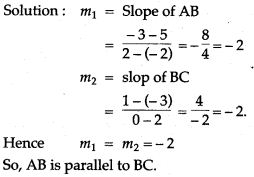
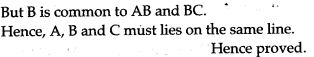
Question 5. By using the distance formula prove that each of the following sets of points are the vertices of a right angled triangle.
(i) (6, 2), (3, -1) and (- 2, 4)
(ii) (-2, 2), (8, -2) and (-4, -3).

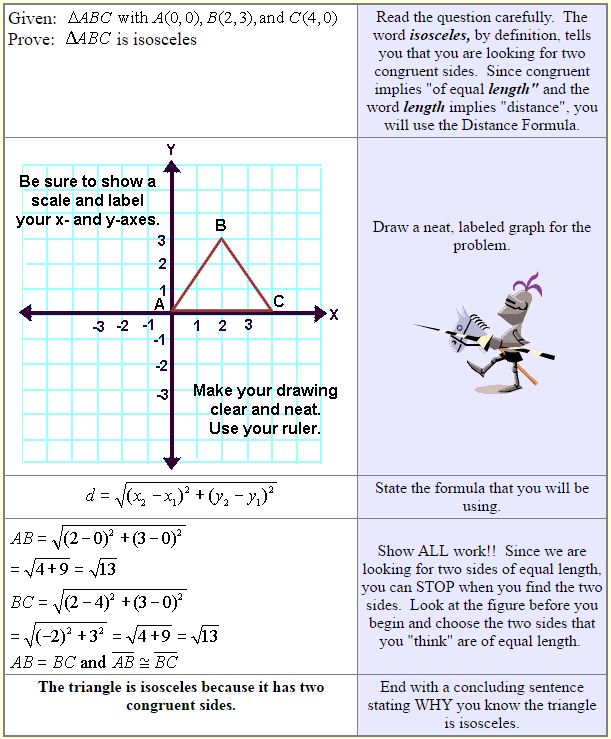
Question 6. Show that each of the triangles whose vertices are given below are isosceles :
(i) (8, 2), (5,-3) and (0,0)
(ii) (0,6), (-5, 3) and (3,1).


Question 7. Show that the quadrilateral with vertices (3, 2), (0, 5), (- 3, 2) and (0, -1) is a square.

![]()


Question 9. If the point (x, y) is at equidistant from the point (a + b, b – a) and (a-b, a + b). Prove that ay = bx.

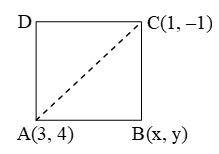
Question 10. Prove that A(4, 3), B(6, 4), C(5, 6) and D(3, 5) are the angular points of a square.



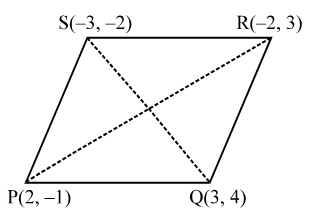
Question 14. Show that the points A(1, 3), B(2, 6), C(5, 7) and D(4, 4) are the vertices of a rhombus.
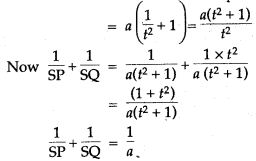

Figure Based Questions

Question 2. Determine the ratio in which the line 3x + y – 9 = 0 divides the line joining (1, 3) and (2, 7).

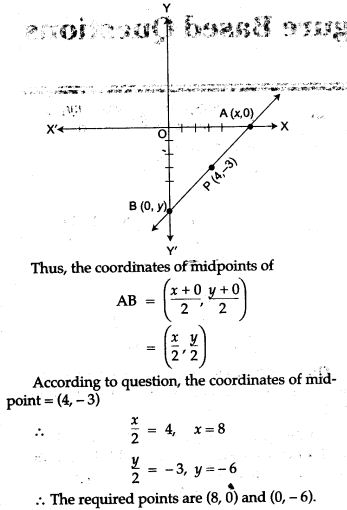
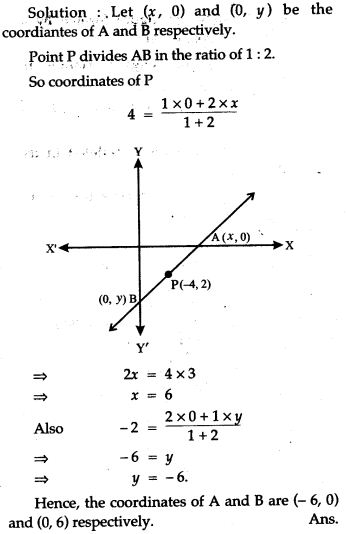
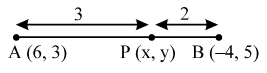
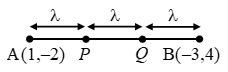
Question 3. The midpoint of the line segment AB shown in the diagram is (4, – 3). Write down the coordinates of A and B.
Solution: Let the coordinates of A and Bare (x, 0) and (0, y).
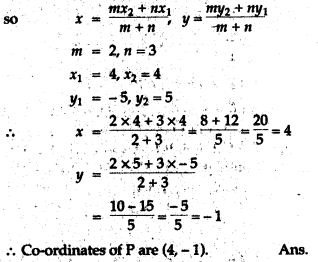
Question 4. The centre ‘O’ of a circle has the coordinates (4, 5) and one point on the circumference is (8, 10). Find the coordinates of the other end of the diameter of the circle through this point.

Hence (0, 0) be the coordinates of the other end.
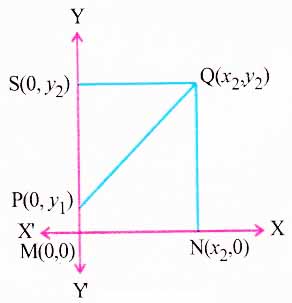
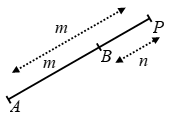
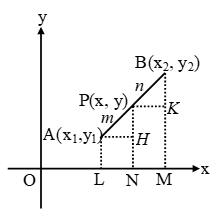
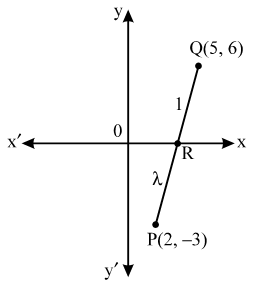
Question 5. In the following figure line APB meets the X-axis at A, Y-axis at B. P is the point (4, -2) and AP : PB = 1 : 2. Write down the coordinates of A and B.
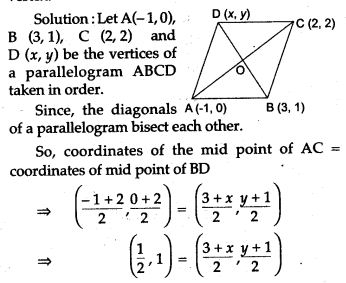
Question 6. The three vertices of a parallelogram taken in order are (-1, 0), (3, 1) and (2, 2) respectively. Find the coordinates of the fourth vertex.
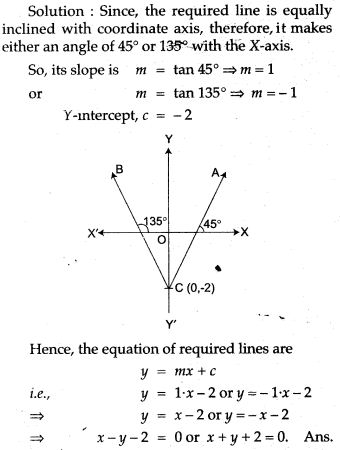
Question 7. Find the equation of a straight line which cuts an intercept – 2 units from Y-axis and being equally inclined to the axis.
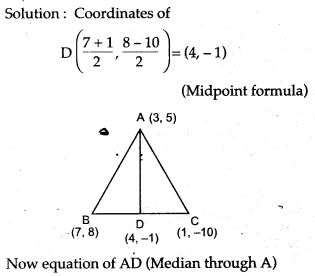
Question 8. In ΔABC, A (3, 5), B (7, 8) and C (1, – 10). Find the equation of the median through A.
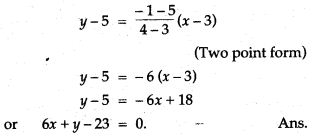
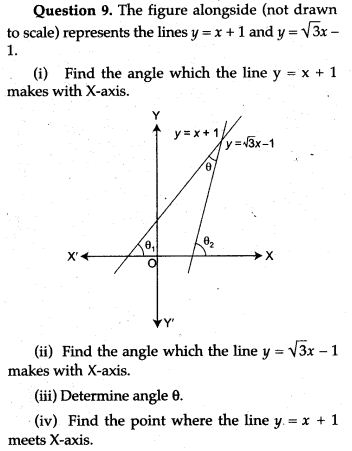

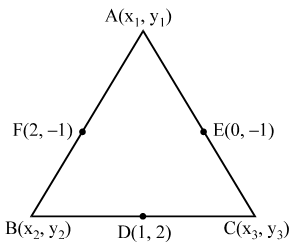
Question 10. In the adjoining figure, write

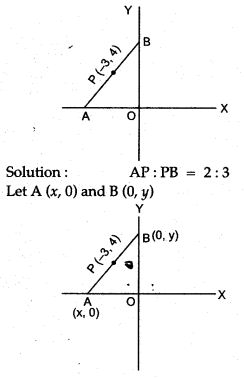
Question 11. In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point P (- 3, 4) on AB divides it in the ratio 2 : 3. Find the coordinates of A and B.

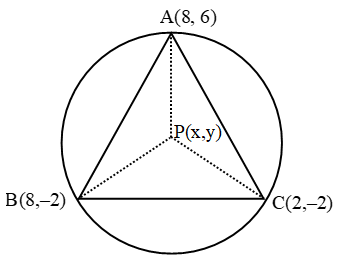
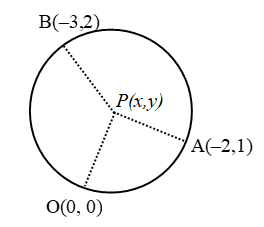
Question 12. Determine the centre of the circle on which the points (1, 7), (7 – 1), and (8, 6) lie. What is the radius of the circle ?
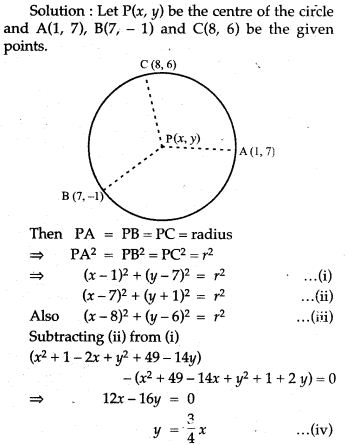

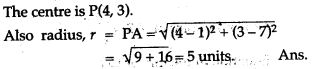
Question 13. Find the image of a point (-1, 2) in the line joining (2, 1) and (- 3, 2).

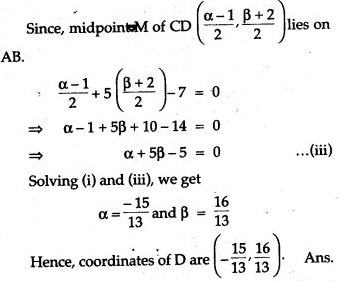
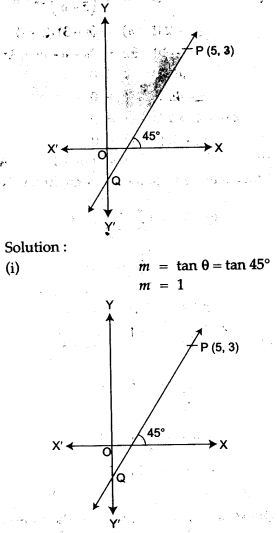
Question 14. The line through P (5, 3) intersects Y axis at Q.
(i) Write the slope of the line.
(ii) Write the equation of the line.
(iii) Find the coordinates of Q.

Question 15. Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line.

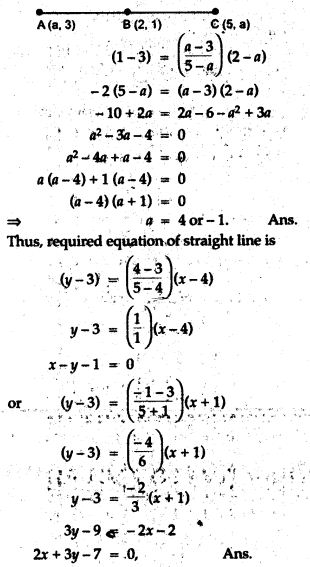
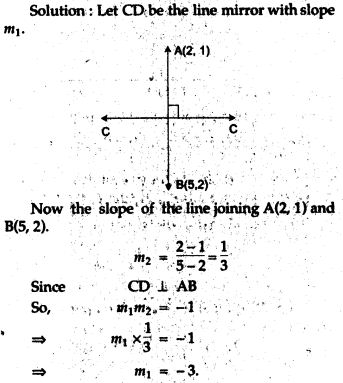
Question 16. If the image of the point (2,1) with respect to the line mirror be (5, 2). Find the equation of the mirror.

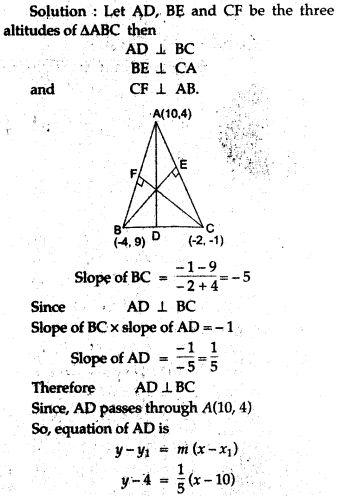
Question 17. The vertices of a triangle are A(10, 4), B(- 4, 9) and C(- 2, -1). Find the
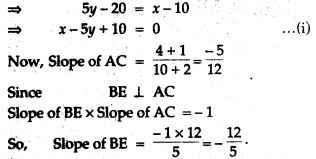

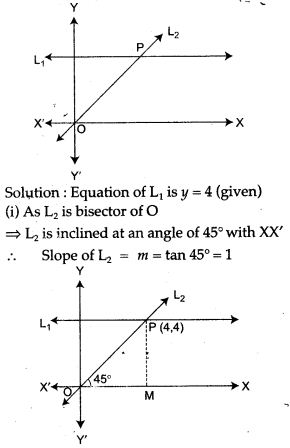
Question 18. Given equation of line L1 is y = 4.
(i) Write the slope of line, if L2 is the bisector of angle O.
(ii) Write the coordinates of point P.
(iii) Find the equation of L2

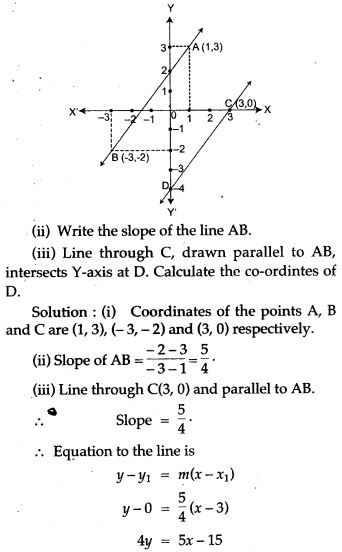
Question 19. From the adjacent figure:
(i) Write the coordinates of the points A, B, and

Graphical Depiction
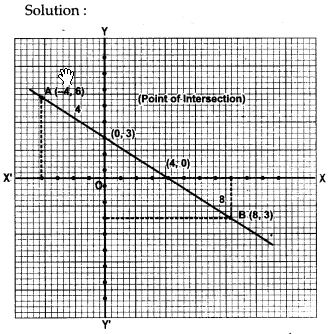
Question 1. Given a line segment AB joining the points A (- 4, 6) and B (8, – 3). Find:
(i) the ratio in which AB is divided by the y- axis.
(ii) find the ordinates of the point of intersection.
(iii) the length of AB.

For More Resources

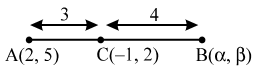
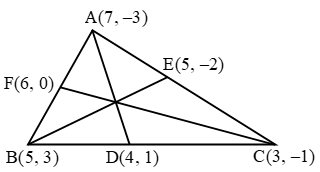
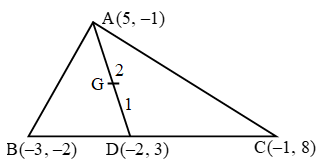
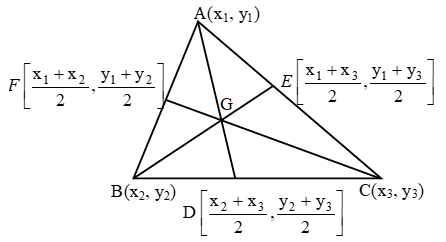

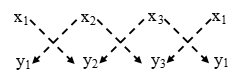 Step III: Compute the sum of the products of numbers at the ends of the lines pointing downwards from left to right and subtract from this sum the sum of the products of numbers at the ends of the lines pointing downward from right to left i.e., compute
Step III: Compute the sum of the products of numbers at the ends of the lines pointing downwards from left to right and subtract from this sum the sum of the products of numbers at the ends of the lines pointing downward from right to left i.e., compute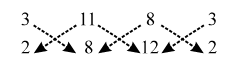 ∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(3 × 8 + 11 ×12 + 8 × 2) – (11 × 2 + 8 × 8 + 3 × 12)|
∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(3 × 8 + 11 ×12 + 8 × 2) – (11 × 2 + 8 × 8 + 3 × 12)|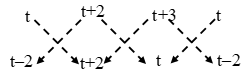 ∴ Area of ∆ABC \(=\frac{1}{2}\left| \{t(t+2)+(t+2)t+(t+3)(t-2)\}-\{(t+2)(t-2)+(t+3)(t+2)+t\times t\} \right|\)
∴ Area of ∆ABC \(=\frac{1}{2}\left| \{t(t+2)+(t+2)t+(t+3)(t-2)\}-\{(t+2)(t-2)+(t+3)(t+2)+t\times t\} \right|\)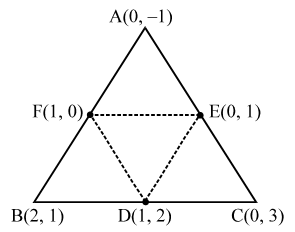 ⇒ Area of ∆DEF = \(\frac { 1 }{ 2 }\) |1 (1 – 0) + 0 (0 – 2) + 1 (2 – 1)|
⇒ Area of ∆DEF = \(\frac { 1 }{ 2 }\) |1 (1 – 0) + 0 (0 – 2) + 1 (2 – 1)|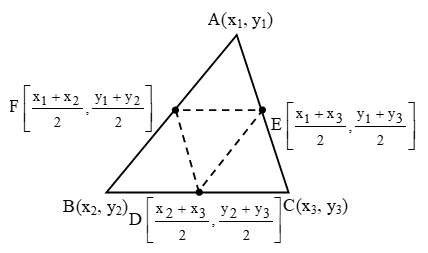 ∆1 = Area of ∆ABC = \(\frac { 1 }{ 2 }\) | x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) |
∆1 = Area of ∆ABC = \(\frac { 1 }{ 2 }\) | x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) |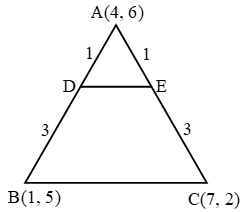 So, the co-ordinates of D and E are
So, the co-ordinates of D and E are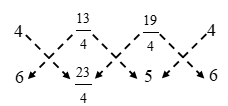
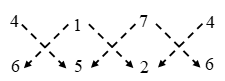 ∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(4 × 5 + 1 × 2 + 7 × 6) – (1 × 6 + 7 × 5 + 4 × 2)|
∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(4 × 5 + 1 × 2 + 7 × 6) – (1 × 6 + 7 × 5 + 4 × 2)|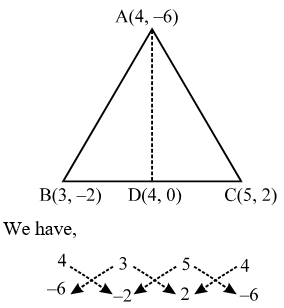 ∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(4 × (– 2) + 3 × 2 + 5 × (– 6)) – (3 × (– 6) + 5 × (–2) + 4 × 2)|
∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(4 × (– 2) + 3 × 2 + 5 × (– 6)) – (3 × (– 6) + 5 × (–2) + 4 × 2)|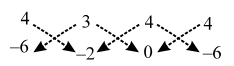 \( \text{ Also of }\Delta \text{ABD = }\left| \{(4\times (-2)+3\times 0+4\times (-6))\}-\{3\times (-6)+4\times (-2)+4\times 0\} \right|\)
\( \text{ Also of }\Delta \text{ABD = }\left| \{(4\times (-2)+3\times 0+4\times (-6))\}-\{3\times (-6)+4\times (-2)+4\times 0\} \right|\)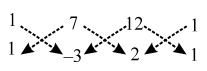 ∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(1× –3 + 7 × 2 + 12 × 1) – (7 × 1 + 12 × (–3) + 1× 2)|
∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(1× –3 + 7 × 2 + 12 × 1) – (7 × 1 + 12 × (–3) + 1× 2)|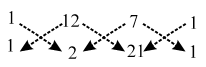 Area of ∆ACD = \(\frac { 1 }{ 2 }\) |(1 ×2 + 12 × 21 + 7 × 1) – (12 × 1 + 7 × 2 + 1 × 21)|
Area of ∆ACD = \(\frac { 1 }{ 2 }\) |(1 ×2 + 12 × 21 + 7 × 1) – (12 × 1 + 7 × 2 + 1 × 21)|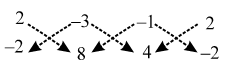 ∴ ∆ = \(\frac { 1 }{ 2 }\) |{2 × 8 + (–3) × 4 + (–1) × (–2)} – {(–3) × (–2) + (–1) × 8 + 2 × 4}|
∴ ∆ = \(\frac { 1 }{ 2 }\) |{2 × 8 + (–3) × 4 + (–1) × (–2)} – {(–3) × (–2) + (–1) × 8 + 2 × 4}|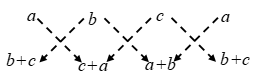 ∴ ∆ = \(\frac { 1 }{ 2 }\) |{a (c + a) + b (a + b) + c (b + c)} – {b (b + c) + c (c + a) + a (a + b)}|
∴ ∆ = \(\frac { 1 }{ 2 }\) |{a (c + a) + b (a + b) + c (b + c)} – {b (b + c) + c (c + a) + a (a + b)}|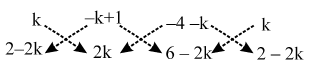 i.e.,
i.e.,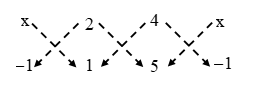 |{x × 1 + 2 × 5 + 4 × (–1)} – {(2 × (–1) + 4 × 1 + x × 5}| = 0
|{x × 1 + 2 × 5 + 4 × (–1)} – {(2 × (–1) + 4 × 1 + x × 5}| = 0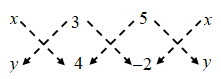 ⇒ \(\frac { 1 }{ 2 }\) |(4x + 3 × (–2) + 5y) – (3y + 20 – 2x)| = 10
⇒ \(\frac { 1 }{ 2 }\) |(4x + 3 × (–2) + 5y) – (3y + 20 – 2x)| = 10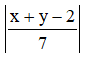 .
.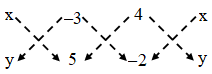 ∴ Area of ∆PBC = \(\frac { 1 }{ 2 }\) |(5x+6+4y)–(–3y+20–2x)|
∴ Area of ∆PBC = \(\frac { 1 }{ 2 }\) |(5x+6+4y)–(–3y+20–2x)|