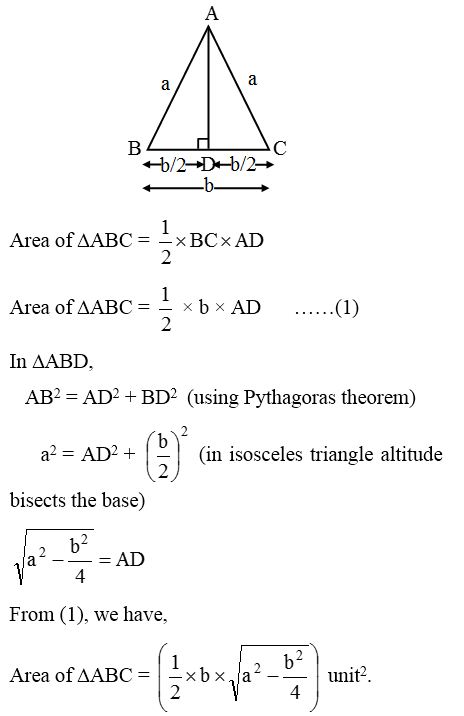
Area Of A Triangle

The area of a triangle, the coordinates of whose vertices are (x1, y1), (x2, y2) and (x3, y3) is
\(\frac { 1 }{ 2 }\) | x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) |
Remark: The area of ∆ABC can also be computed by using the following steps:
Step I: Write the coordinates of the vertices A(x1, y1), B(x2, y2) and C(x3, y3) in three coloums as shown below and augment the coordinates of A(x1, y1) as fourth coloumn.
Step II: Draw broken parallel lines pointing down wards from left to right and right to left.
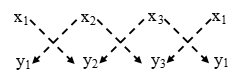 Step III: Compute the sum of the products of numbers at the ends of the lines pointing downwards from left to right and subtract from this sum the sum of the products of numbers at the ends of the lines pointing downward from right to left i.e., compute
Step III: Compute the sum of the products of numbers at the ends of the lines pointing downwards from left to right and subtract from this sum the sum of the products of numbers at the ends of the lines pointing downward from right to left i.e., compute
(x1y2 + x2y3 + x3y1) – (x2y1 + x3y2 + x1y3)
Step IV: Find the absolute of the number obtained in step III and take its half to obtain the area.
Remark: Three points A(x1, y1), B(x2, y2) and C(x3, y3) are collinear iff
Area of ∆ABC = 0 i.e., x1(y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) = 0
Read More:
- Angle Sum Property of a Triangle
- Median and Altitude of a Triangle
- The Angle of An Isosceles Triangle
- Areas of Two Similar Triangles
- To Prove Triangles Are Congruent
- Criteria For Similarity of Triangles
- Construction of an Equilateral Triangle
- Classification of Triangles
Area Of A Triangle With Examples
Type I: On finding the area of a triangle when coordinates of its vertices are given.
Example 1: Find the area of a triangle whose vertices are A(3, 2), B (11, 8) and C(8, 12).
Sol. Let A = (x1, y1) = (3, 2), B = (x2, y2) = (11, 8) and C = (x3, y3) = (8, 12) be the given points. Then,
Area of ∆ABC = \(\frac { 1 }{ 2 }\) | x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) |
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |{3(8 – 12) + 11 (12 – 2) + 8 (2 – 8)}|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(–12 + 110 – 48)| = 25 sq. units
ALTER We have,
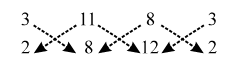 ∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(3 × 8 + 11 ×12 + 8 × 2) – (11 × 2 + 8 × 8 + 3 × 12)|
∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(3 × 8 + 11 ×12 + 8 × 2) – (11 × 2 + 8 × 8 + 3 × 12)|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(24 + 132 + 16) – (22 + 64 + 36)|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) | 172 – 122 | = 25 sq. units
Example 2: Prove that the area of triangle whose vertices are (t, t – 2), (t + 2, t + 2) and (t + 3, t) is independent of t.
Sol. Let A = (x1, y1) = (t, t – 2), B (x2, y2) = (t + 2, t + 2) and C (x3, y3) = (t + 3, t) be the vertices of the given triangle. Then,
Area of ∆ABC = \(\frac { 1 }{ 2 }\) | x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) |
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |{t(t + 2 – t) + (t + 2) (t – t + 2) + (t + 3) (t – 2 – t – 2)}|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |{2t + 2t + 1 – 4t – 12}| = | – 4|
= 4 sq. units
Clearly, area of ∆ABC is independent t.
ALTER We have,
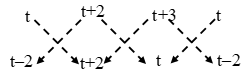 ∴ Area of ∆ABC \(=\frac{1}{2}\left| \{t(t+2)+(t+2)t+(t+3)(t-2)\}-\{(t+2)(t-2)+(t+3)(t+2)+t\times t\} \right|\)
∴ Area of ∆ABC \(=\frac{1}{2}\left| \{t(t+2)+(t+2)t+(t+3)(t-2)\}-\{(t+2)(t-2)+(t+3)(t+2)+t\times t\} \right|\)
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(t2 + 2t + t2 + 2t + t2 + t – 6) – (t2 – 4 + t2 + 5t + 6 + t2)|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) | (3t2 + 5t – 6) – (3t2 + 5t + 2)|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) | (–6 – 2)|
⇒ Area of ∆ABC = 4 sq. units
Hence, Area of ∆ABC is independent of t.
Example 3: Find the area of the triangle formed by joining the mid-point of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of area of the triangle formed to the area of the given triangle.
Sol. Let A (0, –1), B(2, 1) and C(0, 3) be the vertices of ∆ABC. Let D, E, F be the mid-points of sides BC, CA and AB respectively. Then, the coordinates of D, E and F are (1, 2), (0, 1) and (1, 0) respectively.
Now,
Area of ∆ABC = \(\frac { 1 }{ 2 }\) | x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) |
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) | 0(1 – 3) + 2 (3 – (–1)) + 0(0 – 1)|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) | 0 + 8 + 0 | = 4 sq. units
Area of ∆DEF = \(\frac { 1 }{ 2 }\) | x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) |
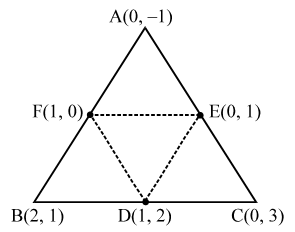 ⇒ Area of ∆DEF = \(\frac { 1 }{ 2 }\) |1 (1 – 0) + 0 (0 – 2) + 1 (2 – 1)|
⇒ Area of ∆DEF = \(\frac { 1 }{ 2 }\) |1 (1 – 0) + 0 (0 – 2) + 1 (2 – 1)|
⇒ Area of ∆DEF = \(\frac { 1 }{ 2 }\) |1 + 1| = 1 sq. units
∴ Area of ∆DEF : Area of ∆ABC = 1 : 4
Example 4: If D, E and F are the mid-points of sides BC, CA and AB respectively of a ∆ABC, then using coordinate geometry prove that
Area of ∆DEF = \(\frac { 1 }{ 4 }\) (Area of ∆ABC)
Sol. Let A(x1, y1), B(x2, y2) and C(x3, y3) be the vertices of ∆ABC. Then, the coordinates of D, E and F are
\(\left( \frac{{{x}_{2}}+{{x}_{3}}}{2},\ \frac{{{y}_{2}}+{{y}_{3}}}{2} \right)\left( \frac{{{x}_{1}}+{{x}_{3}}}{2},\ \frac{{{y}_{1}}+{{y}_{3}}}{2} \right)\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\ \frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\text{ respectively}\text{.}\)
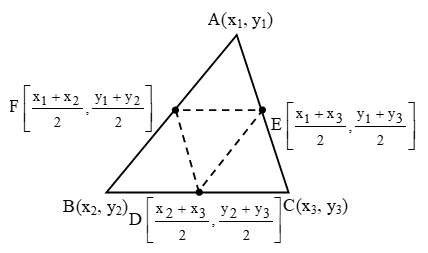 ∆1 = Area of ∆ABC = \(\frac { 1 }{ 2 }\) | x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) |
∆1 = Area of ∆ABC = \(\frac { 1 }{ 2 }\) | x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) |
∆2 = Area of ∆DEF
\(=\frac{1}{2}\left| \left( \frac{{{x}_{2}}+{{x}_{3}}}{2} \right)\left( \frac{{{y}_{1}}+{{y}_{3}}}{2}-\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)+\left( \frac{{{x}_{1}}+{{x}_{3}}}{2} \right) \right.\left( \frac{{{y}_{1}}+{{y}_{2}}}{2}-\frac{{{y}_{2}}+{{y}_{3}}}{2} \right)+\left( \frac{{{x}_{1}}+{{x}_{2}}}{2} \right)\left. \left( \frac{{{y}_{2}}+{{y}_{3}}}{2}-\frac{{{y}_{1}}+{{y}_{3}}}{2} \right) \right|\)
⇒ ∆2 = \(\frac { 1 }{ 8 }\) |(x2 + x3)(y3 – y2) + (x1 + x3)(y1 – y3) + (x1 + x2)(y2 – y1)|
⇒ ∆2 = \(\frac { 1 }{ 8 }\) |x1(y1 – y3 + y2 – y1) + x2 (y3 – y2 + y2 – y1) + x3 (y3 – y2 + y1 – y3)|
⇒ ∆2 = \(\frac { 1 }{ 8 }\) |x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)|
⇒ ∆2 = \(\frac { 1 }{ 4 }\) (Area of ∆ABC) = \(\frac { 1 }{ 4 }\) ∆1
Hence, Area of ∆DEF = \(\frac { 1 }{ 4 }\) (Area of ∆ABC)
Example 5: The vertices of ∆ABC = are A (4, 6), B(1, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively such that \( \frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4} \) . Calculate the area of ∆ADE and compare it with the area of ∆ABC.
Sol. We have,
\( \frac{AD}{AB}=\frac{AE}{AC}=\frac{1}{4} \)
\( \Rightarrow \frac{AB}{AD}=\frac{AC}{AE}=4\)
\( \Rightarrow \frac{AD+DB}{AD}=\frac{AE+EC}{AE}=4 \)
\( \Rightarrow 1+\frac{DB}{AD}=1+\frac{EC}{AE}=4 \)
\( \Rightarrow \frac{DB}{AD}=\frac{EC}{AE}=3\Rightarrow \frac{AD}{DB}=\frac{AE}{EC}=\frac{1}{3} \)
⇒ AD : DB = AE : EC = 1 : 3
⇒ D and E divide AB and AC respectively in the ratio 1 : 3.
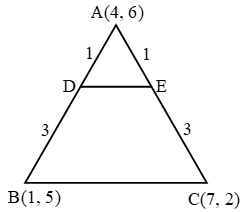 So, the co-ordinates of D and E are
So, the co-ordinates of D and E are
\(\left( \frac{1+12}{1+3},\ \frac{5+18}{1+3} \right)=\left( \frac{13}{4},\ \frac{23}{4} \right)\text{ and }\left( \frac{7+12}{1+3},\ \frac{2+18}{1+3} \right)=\left( \frac{19}{4},\ 5 \right)\text{ respectively}\text{.}\)
We have,
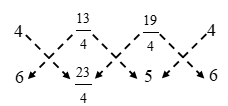
∴ Area of ∆ADE
\( =\frac{1}{2}\left| \left( 4\times \frac{23}{4}+\frac{13}{4}\times 5+\frac{19}{4}\times 6 \right)-\left( \frac{13}{4}\times 6+\frac{19}{4}\times \frac{23}{4}+4\times 5 \right) \right| \)
\( =\frac{1}{2}\left| \left( \frac{92}{4}+\frac{65}{4}+\frac{114}{4} \right)-\left( \frac{78}{4}+\frac{437}{16}+20 \right) \right| \)
\( =\frac{1}{2}\left| \frac{271}{4}-\frac{1069}{16} \right| \)
\( =\frac{1}{2}\times \frac{15}{16}=\frac{15}{32}sq.\text{ }untis. \)
Also, we have
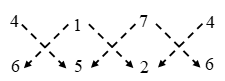 ∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(4 × 5 + 1 × 2 + 7 × 6) – (1 × 6 + 7 × 5 + 4 × 2)|
∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(4 × 5 + 1 × 2 + 7 × 6) – (1 × 6 + 7 × 5 + 4 × 2)|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(20 + 2 + 42) – (6 + 35 + 8)|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |64 – 49| = sq. units
\( \frac{Area\ of\ \Delta ADE}{Area\ of\ \Delta ABC}=\frac{15/32}{15/2}=\frac{1}{16}\)
Hence, Area of ∆ADE : Area of ∆ABC = 1 : 16.
Example 6: If A(4, –6), B(3, –2) and C(5, 2) are the vertices of ∆ABC, then verify the fact that a median of a triangle ABC divides it into two triangle of equal areas.
Sol. Let D be the mid-point of BC. Then, the coordinates of D are (4, 0).
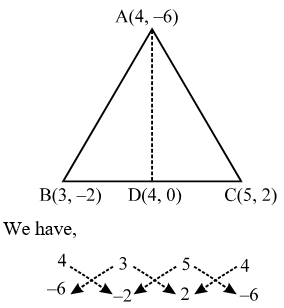 ∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(4 × (– 2) + 3 × 2 + 5 × (– 6)) – (3 × (– 6) + 5 × (–2) + 4 × 2)|
∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(4 × (– 2) + 3 × 2 + 5 × (– 6)) – (3 × (– 6) + 5 × (–2) + 4 × 2)|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |( –8 + 6 – 30) – (–18 – 10 + 8)|
⇒ Area of ∆ABC = \(\frac { 1 }{ 2 }\) | –32 + 20 | = 6 sq. units
Also, We have
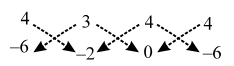 \( \text{ Also of }\Delta \text{ABD = }\left| \{(4\times (-2)+3\times 0+4\times (-6))\}-\{3\times (-6)+4\times (-2)+4\times 0\} \right|\)
\( \text{ Also of }\Delta \text{ABD = }\left| \{(4\times (-2)+3\times 0+4\times (-6))\}-\{3\times (-6)+4\times (-2)+4\times 0\} \right|\)
⇒ Area of ∆ABD = \(\frac { 1 }{ 2 }\) |(–8 + 0 + 26) – (–18 – 8 + 0)|
⇒ Area of ∆ABD = \(\frac { 1 }{ 2 }\) |(–32 + 26)| = 3 sq. units
\(\Rightarrow \frac{Area\ of\ \Delta ABC}{Area\ of\ \Delta ABD}=\frac{6}{3}=\frac{2}{1}\)
⇒ Area of ∆ABC = 2 (Area of ∆ABD)
TypeII: On finding the area of a quadrilateral when coordinates of its vertices are given
Example 7: Find the area of the quadrilateral ABCD whose vertices are respectively A(1, 1), B(7, –3), C(12, 2) and D(7, 21).
Sol. Area of quadrilateral ABCD = | Area of ∆ABC | + | Area of ∆ACD |
We have,
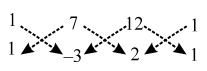 ∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(1× –3 + 7 × 2 + 12 × 1) – (7 × 1 + 12 × (–3) + 1× 2)|
∴ Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(1× –3 + 7 × 2 + 12 × 1) – (7 × 1 + 12 × (–3) + 1× 2)|
Area of ∆ABC = \(\frac { 1 }{ 2 }\) |(–3 + 14 + 12) – (7 – 36 + 2)|
Area of ∆ABC = \(\frac { 1 }{ 2 }\) |23 + 27| = 25 sq. units
Also, we have
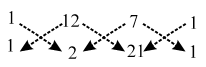 Area of ∆ACD = \(\frac { 1 }{ 2 }\) |(1 ×2 + 12 × 21 + 7 × 1) – (12 × 1 + 7 × 2 + 1 × 21)|
Area of ∆ACD = \(\frac { 1 }{ 2 }\) |(1 ×2 + 12 × 21 + 7 × 1) – (12 × 1 + 7 × 2 + 1 × 21)|
Area of ∆ACD = \(\frac { 1 }{ 2 }\) |(2 + 252 + 7) – (12 + 14 + 21)|
Area of ∆ACD = \(\frac { 1 }{ 2 }\) |261 – 47| = 107 sq. units
Area of quadrilateral ABCD = 25 + 107 = 132 sq. units
Type III: On collinearity of three points
Three points A(x1, y1), B(x2, y2) and C(x3, y3) are collinear if
Area of ∆ABC = 0 i.e., x1(y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2) = 0
Example 8: Prove that the points (2, – 2), (–3, 8) and (–1, 4) are collinear.
Sol. Let ∆ be the area of the triangle formed by the given points.
We have,
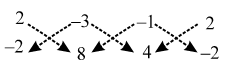 ∴ ∆ = \(\frac { 1 }{ 2 }\) |{2 × 8 + (–3) × 4 + (–1) × (–2)} – {(–3) × (–2) + (–1) × 8 + 2 × 4}|
∴ ∆ = \(\frac { 1 }{ 2 }\) |{2 × 8 + (–3) × 4 + (–1) × (–2)} – {(–3) × (–2) + (–1) × 8 + 2 × 4}|
⇒ ∆ = \(\frac { 1 }{ 2 }\) |(16 – 12 + 2) – (6 – 8 + 8)|
⇒ ∆ = \(\frac { 1 }{ 2 }\) |6 – 6| = 0
Hence, given points are collinear.
Example 9: Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear.
Sol. Let ∆ be the area of the triangle formed by the points (a, b + c), (b, c + a) and (c, a + b).
We have,
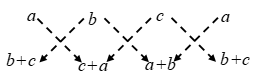 ∴ ∆ = \(\frac { 1 }{ 2 }\) |{a (c + a) + b (a + b) + c (b + c)} – {b (b + c) + c (c + a) + a (a + b)}|
∴ ∆ = \(\frac { 1 }{ 2 }\) |{a (c + a) + b (a + b) + c (b + c)} – {b (b + c) + c (c + a) + a (a + b)}|
⇒ ∆ = \(\frac { 1 }{ 2 }\) |(ac + a2 + ab + b2 + bc + c2) – (b2 + bc + c2 + ca + a2 + ab)|
⇒ ∆ = 0
Hence, the given points are collinear.
Type IV: On Finding the desired result or unknown when three points are collinear
Example 10: For what value of k are the points (k, 2 – 2k), (–k + 1, 2k) and (–4 – k, 6 – 2k) are collinear ?
Sol. Given points will be collinear, if area of the triangle formed by them is zero.
We have,
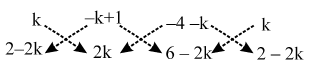 i.e.,
i.e.,
|{2k2 + (–k + 1) (6 – 2k) + (–4 – k) (2 – 2k)} – {(–k + 1) (2 – 2k) + (–4 – k) (2k) + k (6 – 2k)}| = 0
⇒ |(2k2 + 6 –8k + 2k2 + k2 + 6k – 8) – (2 – 4k + k2 – 8k – 2k2 + 6k – 2k2)| = 0
⇒ (6k2 – 2k – 2) – (–2k2 – 6k + 2) = 0
⇒ 8k2 + 4k – 4 = 0
⇒ 2k2 + k – 1 = 0 ⇒ (2k – 1) (k + 1) = 0
⇒ k = 1/2 or, k = – 1
Hence, the given points are collinear for
⇒ k = 1/2 or, k = – 1.
Example 11: For what value of x will the points (x, –1), (2, 1) and (4, 5) lie on a line ?
Sol. Given points will be collinear if the area of the triangle formed by them is zero.
∴ Area of the triangle = 0
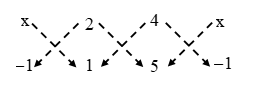 |{x × 1 + 2 × 5 + 4 × (–1)} – {(2 × (–1) + 4 × 1 + x × 5}| = 0
|{x × 1 + 2 × 5 + 4 × (–1)} – {(2 × (–1) + 4 × 1 + x × 5}| = 0
⇒ (x + 10 – 4) – (–2 + 4 + 5x) = 0
⇒ (x + 6) – (5x + 2) = 0
⇒ – 4x + 4 = 0
⇒ x = 1
Hence, the given points lies on a line, if x = 1.
Type V: Mixed problems based upon the concept of area of a triangle
Example 12: If the coordinates of two points A and B are (3, 4) and (5, – 2) respectively. Find the coordniates of any point P, if PA = PB and Area of ∆PAB = 10.
Sol. Let the coordinates of P be (x, y). Then,
PA = PB
⇒ PA2 = PB2
⇒ (x – 3)2 + (y– 4)2 = (x – 5)2 + (y + 2)2
⇒ x – 3y – 1 = 0 ….(1)
Now, Area of ∆PAB = 10
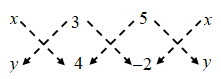 ⇒ \(\frac { 1 }{ 2 }\) |(4x + 3 × (–2) + 5y) – (3y + 20 – 2x)| = 10
⇒ \(\frac { 1 }{ 2 }\) |(4x + 3 × (–2) + 5y) – (3y + 20 – 2x)| = 10
⇒ |(4x + 5y – 6) – (–2x + 3y + 20)| = 20
⇒ |6x + 2y – 26| = ± 20 ⇒ 6x + 2y – 26 = ± 20
⇒ 6x + 2y – 46 = 0 or, 6x + 2y – 6 = 0
⇒ 3x + y – 23 = 0 or, 3x + y – 3 = 0
Solving x – 3y – 1 = 0 and 3x + y – 23 = 0
we get x = 7, y = 2.
Solving x – 3y – 1 = 0 and 3x + y – 3 = 0,
we get x = 1, y = 0.
Thus, the coordinates of P are (7, 2) or (1, 0).
Example 13: The coordinates of A, B, C are (6, 3), (–3, 5) and (4, – 2) respectively and P is any point (x, y). Show that the ratio of the areas of triangle PBC and ABC is 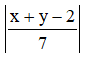 .
.
Sol. We have,
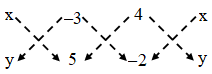 ∴ Area of ∆PBC = \(\frac { 1 }{ 2 }\) |(5x+6+4y)–(–3y+20–2x)|
∴ Area of ∆PBC = \(\frac { 1 }{ 2 }\) |(5x+6+4y)–(–3y+20–2x)|
⇒ Area of ∆PBC = \(\frac { 1 }{ 2 }\) |5x + 6 + 4y + 3y – 20 + 2x|
⇒ Area of ∆PBC = \(\frac { 1 }{ 2 }\) |7x + 7y – 14|
⇒ Area of ∆PBC = \(\frac { 7 }{ 2 }\) |x + y– 2|
⇒ Area of ∆PBC = \(\frac { 7 }{ 2 }\) |6 + 3 – 2| \(\left[ \text{Replacing}\ \text{x}\ \text{by}\ \text{6}\ \text{and}\ \text{y}=\text{3in}\ \text{Area}\ \text{of}\ \text{ }\!\!\Delta\!\!\text{ PBC} \right]\)
⇒ Area of ∆ABC = \(\frac { 49 }{ 2 }\)
\( \frac{Area\ of\ \Delta PBC}{Area\ of\ \Delta ABC}=\frac{\frac{7}{2}|x+y-2|}{\frac{49}{2}} \)
\( =\frac{|x+y-2|}{7}=\left| \frac{x+y-2}{7} \right| \)