How Do You Find The Angle Of An Isosceles Triangle

Theorem: Angles opposite to equal sides of an isosceles triangle are equal.
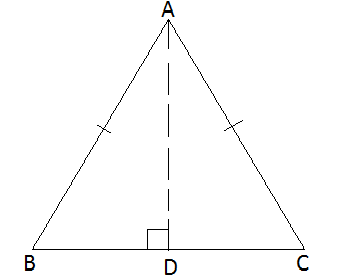
Given: In ∆ABC, AB = AC
To Prove: ∠B = ∠C
Construction: Draw AD, bisector of ∠A
∴ ∠1 = ∠2
Proof: In ∆ADB & ∆ADC
AD = AD (Common)
∠1 = ∠2 (by construction)
AB = AC
By SAS, ∆ADB ≅ ∆ADC
∴ ∠B = ∠C (c.p.c.t.) Proved.
Note: Other result: ∠ADB = ∠ADC (c.p.c.t.)
But ∠ADB + ∠ADC = 180° (linear pair)
∴ ∠ADB = ∠ADC = 90° ⇒ AD ⊥ BC
and BD = DC (c.p.c.t.) ⇒ AD is median
∴ we can say AD is perpendicular bisector of BC or we can say in isosceles ∆, median is angle bisector and perpendicular to base also.
Read More:
- Angle Sum Property of a Triangle
- Median and Altitude of a Triangle
- Areas of Two Similar Triangles
- Area of A Triangle
- To Prove Triangles Are Congruent
- Criteria For Similarity of Triangles
- Construction of an Equilateral Triangle
- Classification of Triangles
Angle Of An Isosceles Triangle Example Problems With Solutions
Example 1: Find ∠BAC of an isosceles triangle in which AB = AC and ∠B = 1/3 of right angle.
Solution:

Example 2: In isosceles triangle DEF, DE = EF and ∠E = 70° then find other two angles.

Solution:

Example 3: ∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see fig.). If AD is extended to intersect BC at P. Show that
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.

Solution:


Example 4: Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆PQR (see figure ). Show that:
(i) ∆ABM ≅ ∆PQN (ii) ∆ABC ≅ ∆PQR

Solution:
