Triangles Archives

How Do You Prove Triangles Are Congruent

December 11, 2020December 11, 2020 by Veerendra

How Do You Prove Triangles Are Congruent

https://www.youtube.com/watch?v=GmS-p1S_t5E

Congruent Figures

Two figures/objects are said to be congruent if they are exactly of the same shape and size. The relationship between two congruent figures is called congruence. We use the symbol ≅ for ‘congruent to’.

Congruence among line segments: Two line segments are congruent if they have the same length.

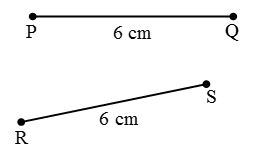
Thus, line segment PQ ≅ line segment RS as PQ = RS = 6 cm.
Congruence of Angles: Two angles are congruent if they have the same measure.

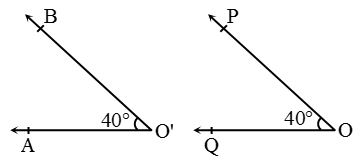
Thus, ∠AO’B ≅ ∠QOP,
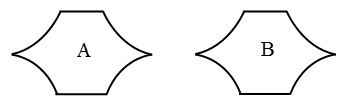
as m ∠AO’B = m ∠QOP = 40°.
Congruence of plane figures: Two plane figures A and B are congruent as they superpose each other. We can write it as figure A ≅ figure B.
Congruence of squares: Two squares are congruent if they have same side length.

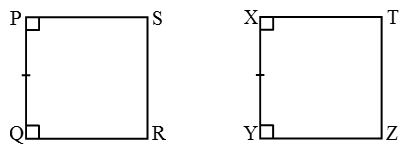
Square PQRS ≅ Square XYZT as PQ = XY.
Congruence of rectangles: Two rectangles are said to be congruent if they have the same length and breadth.

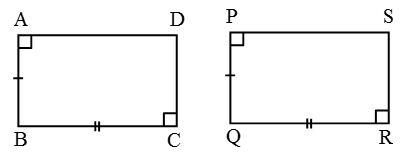
Rectangle ABCD ≅ Rectangle PQRS as
AB = PQ and BC = QR.
Congruence of circles: Two circles are congruent if they have the same radius.

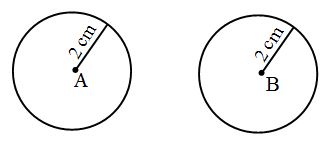
Circle A ≅ Circle B, as radius of A = radius of B = 2 cm.

Congruence of Triangles

Two triangles are congruent if they are copies of each other, and when superposed they cover each other exactly.
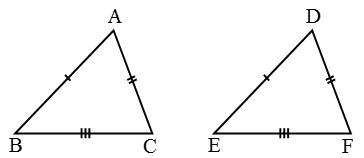How Do You Prove Triangles Are Congruent 7 ∆ABC and ∆DEF have the same size and shape. They are congruent. So we would express this as ∆ABC ∆DEF. This means that, when we place ∆DEF on ∆ABC, D falls on A, E falls on B and F falls on C, also $\overline { DE }$ falls along $\overline { AB } ,\overline { EF }$ falls along $\overline { BC }$ and $\overline { DF }$ falls along $\overline { AC }$.

Corresponding angles are: ∠A and ∠D, ∠B and ∠E, ∠C and ∠F.
Corresponding vertices are: A and D, B and E, C and F.
Corresponding sides are: $\overline { AB }$ and $\overline { DE } ,\overline { BC }$ and $\overline { EF } ,\overline { AC }$ and $\overline { DF }$.

Hence, three sides and three angles are the six matching parts for the congruence of triangles.

Examples:

1. Write the correspondence between the vertices, sides and angles of the triangles XYZ and MLN, if ∆XYZ ≅ ∆MLN.
Solution:
By the order of letters, we find that
X ↔ M, Y ↔ L and Z ↔ N
∴ XY = ML, YZ = LN, XZ = MN
Also ∠X = ∠M, ∠Y = ∠L and ∠Z = ∠N.

2. In following pairs of triangles, find the correspondence between the triangles so that they are congruent.
In ∆PQR: PQ = 4 cm, QR = 5 cm, PR = 6 cm, ∠P = 60°, ∠Q = 80°, ∠R = 40°.
In ∆XYZ: XY = 6 cm, ZY = 5 cm, XZ = 4 cm, ∠X = 60°, ∠Y = 40°, ∠Z = 80°.
Solution:
Let us draw the triangles and write the measures of their corresponding parts along with them.
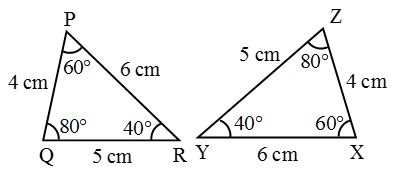
How Do You Prove Triangles Are Congruent 8
From the above figures, we note that
PQ = XZ, QR = YZ, PR = XY
and ∠P = ∠X, ∠Q = ∠Z, ∠R = ∠Y
∴ P ↔ X, Q ↔ Z and R ↔ Y
Hence, ∆PQR ≅ ∆XZY

Read More:

Some more results based on congruent triangles:

If two sides of a triangle are unequal, then the longer side has the greater angle opposite to it.
In a triangle, the greater angle has the longer side opposite to it.
Of all the line segments that can be drawn to a given line, from a point not lying on it, the perpendicular line segment is the shortest.
The sum of any two sides of a triangle is greater than its third side.
The difference between any two sides of a triangle is less than its third side.
Exterior angle is greater than one opposite interior angle.

Congruent Triangles Example Problems With Solutions

Example 1: Find the relation between angles in figure.
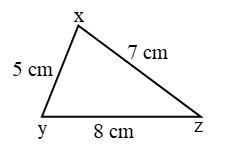
How Do You Prove Triangles Are Congruent 9
Solution: ∵ yz > xz > xy
⇒∠x > ∠y > ∠z.
(∵ Angle opposite to longer side is greater)

Example 2: Find the relation between the sides of triangle in figure.
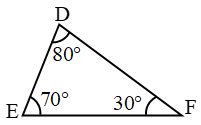
How Do You Prove Triangles Are Congruent 10
Solution: ∵ ∠D > ∠E > ∠F
∴EF > DF > DE
{∵ side opposite to greater angle is longer}

Example 3: Find ∠ACD then what is the relation between (i) ∠ACD, ∠ABC (ii) ∠ACD & ∠A
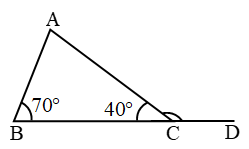
How Do You Prove Triangles Are Congruent 11
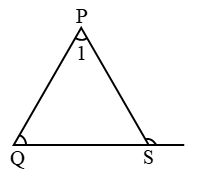
Solution: ∠ACD + 40° = 180° (linear pair)
∠ACD = 140°
also ∠A + ∠B = ∠ACD
(exterior angle = sum of opp. interior angles)
⇒ ∠A + 70° = 140° ⇒ ∠A = 140° – 70°
⇒ ∠A = 70°
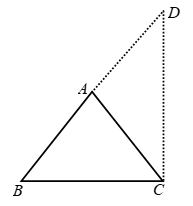
Now ∠ACD > ∠B
∠ACD > ∠A

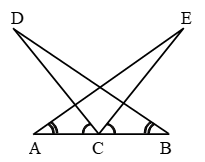
Example 4: In Fig. ∠E > ∠A and ∠C > ∠D. Prove that AD > EC.
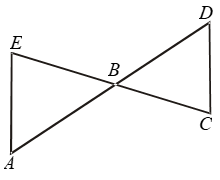
How Do You Prove Triangles Are Congruent 12
Solution: In ∆ABE, it is given that
∠E > ∠A
⇒ AB > BE …. (i)
In ∆BCD, it is given that
∠C > ∠D
⇒ BD > BC …. (ii)
Adding (i) and (ii), we get
AB + BD > BE + BC ⇒AD > EC

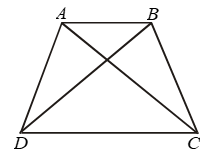
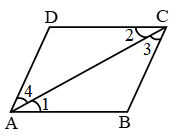
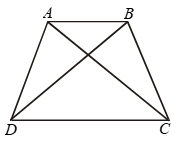
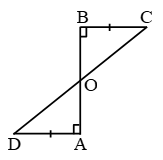
Example 5: AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠A > ∠C.
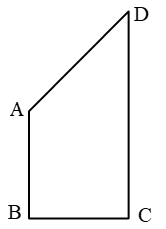
How Do You Prove Triangles Are Congruent 13
Solution: Draw diagonal AC.

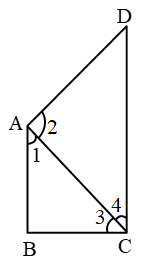
In ∆ABC, AB < BC {∵ AB is smallest}
⇒ ∠3 < ∠1 ……(1)
{angle opp. to longer side is larger}
Also in ∆ADC
AD < CD ∵ CD is longest
⇒ ∠4 < ∠2 …..(2)
adding equation (1) & (2)
∠3 + ∠4 < ∠1 + ∠2
∠C < ∠A
or ∠A > ∠C Proved.

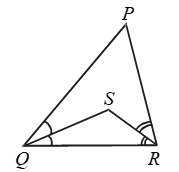
Example 6: In given figure, PR > PQ and PS bisects ∠QPR. Prove that ∠PSR > ∠PSQ.
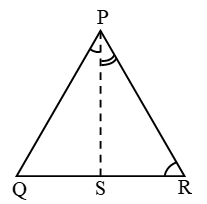
How Do You Prove Triangles Are Congruent 15
Solution: In ∆PQR, PR > PQ
⇒ ∠Q > ∠R ……(1)
{angle opposite to longer side is greater}
and ∠1 = ∠2 (∵ PS is ∠bisector) ….(2)

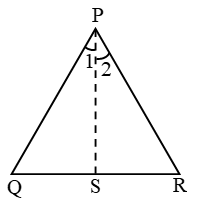
Now for ∆PQS, ∠PSR = ∠Q + ∠1 ….(3)
{exterior angle = sum of opposite interior angle}
How Do You Prove Triangles Are Congruent 17
& for ∆PSR, ∠PSQ = ∠R + ∠2 ….(4)
By equation (1), (2), (3), (4), ∠PSR > ∠PSQ
Proved.

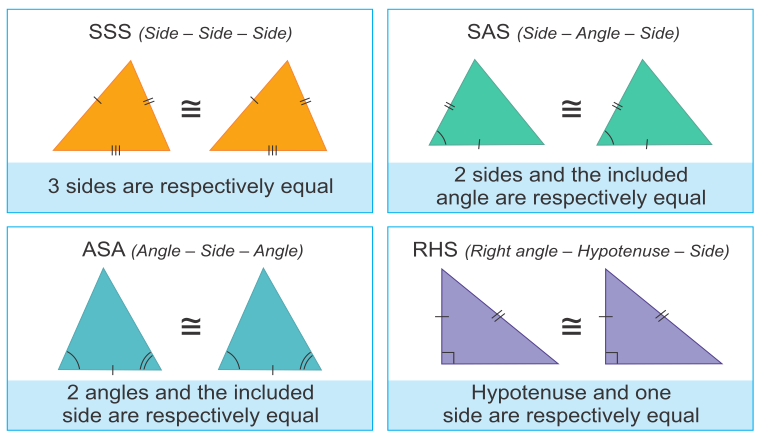
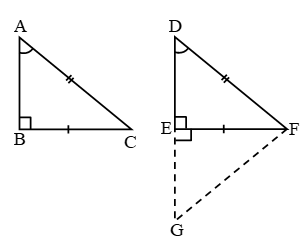
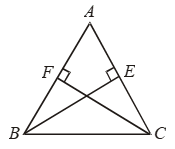
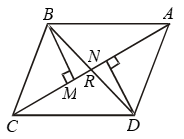
Example 7: AD, BE and CF, the altitudes of ∆ABC are equal. Prove that ∆ABC is an equilateral triangle.
Solution:
In right triangles BCE and BFC, we have
Hyp. BC = Hyp. BC
BE = CF [Given]
So, by RHS criterion of congruence,
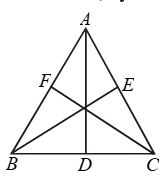
How Do You Prove Triangles Are Congruent 18
ΔBCE ≅ ΔBFC.
⇒ ∠B = ∠C
⇒ AC = AB …. (i)
[∵ Sides opposite to equal angles are equal]
Similarly, ΔABD ≅ ΔABE
⇒ ∠B = ∠A
[∵ Corresponding parts of congruent triangles are equal]
⇒ AC = BC …. (ii)
[∵ Sides opposite to equal angles are equal]
From (i) and (ii), we get
AB = BC = AC
Hence, ΔABC is an equilateral triangle.

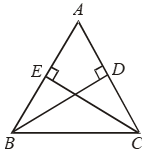
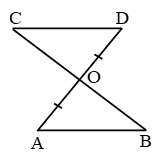
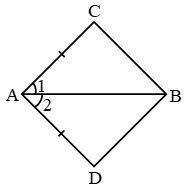
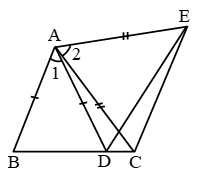
Example 8: In Fig. AD = BC and BD = CA.
How Do You Prove Triangles Are Congruent 19
Prove that ∠ADB = ∠BCA and ∠DAB = ∠CBA.
Solution:
In triangles ABD and ABC, we have
AD = BC [Given]
BD = CA [Given]
and AB = AB [Common]
So, by SSS congruence criterion, we have
ΔABD ≅ ΔCBA ⇒ ∠DAB = ∠ABC
[∵ corresponding parts of congruent triangles are equal]
⇒ ∠DAB = ∠CBA

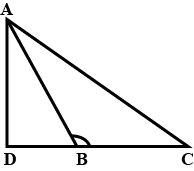
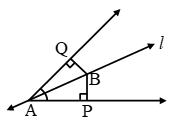
Example 9: In Fig. PQ > PR. QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ > SR.
$D:\Work\Aplustopper\Content\Maths\How Do You Prove Triangles Are Congruent 20.png$
Solution:
In ΔPQR, we have
PQ > PR [Given]
⇒ ∠PRQ > ∠PQR
[∵ Angle opp. to larger side of a triangle is greater]
⇒ $\frac { 1 }{ 2 } $∠PRQ > $\frac { 1 }{ 2 } $∠PQR
[∵ RS and QS are bisectors of ∠PRQ and ∠PQR respectively]
⇒ ∠SRQ > ∠SQR
⇒ SQ > SR
[∵ Side opp. to greater angle is larger]

Example 10: In Fig.
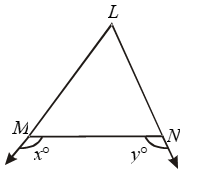
How Do You Prove Triangles Are Congruent 21
if x > y, show that ∠M > ∠N.
Solution:
We have,
∠LMN + xº = 180º …. (i)
[Angles of a linear pair]
⇒ ∠LNM + yº = 180º …. (ii)
[Angles of a linear pair]
∴ ∠LMN + xº = ∠LNM + yº
But x > y. Therefore,
∠LMN < ∠LNM
⇒ ∠LNM > ∠LMN
⇒ LM > LN
[∵ Side opp. to greater angle is larger]

Example 11: In Fig. AB > AC. Show that AB > AD.
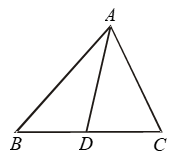
How Do You Prove Triangles Are Congruent 22
Solution:
In ΔABC, we have
AB > AC [Given]
⇒ ∠ACB > ∠ABC …. (i)
[∵ Angle opp. to larger side is greater]
Now, in ΔACD, CD is produced to B, forming an ext ∠ADB.
⇒ ∠ADB > ∠ACD
[∵ Exterior angle of Δ is greater than each of interior opp. angle]
⇒ ∠ADB > ∠ACB … (ii)
[∴ ∠ACD = ∠ACB]
From (i) and (ii), we get
∠ADB > ∠ABC
⇒ ∠ADB > ∠ABD [∵ ∠ABC = ∠ABD]
⇒ AB > AD
[∵ Side opp. to greater angle is larger]

Example 12: Prove that any two sides of a triangle are together greater than twice the median drawn to the third side.
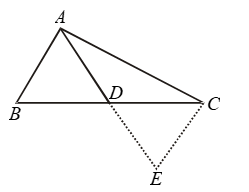
How Do You Prove Triangles Are Congruent 23
Solution:
To prove: AB + AC > 2 AD
Construction: Produce AD to E such that AD = DE. Join EC.
Proof: In Δ’s ADB and EDC, we have
AD = DE [By construction]
BD = DC [∵ D is the mid point of BC]
and, ∠ADB = ∠EDC [Vertically opp. angles]
So, by SAS criterion of congruence
⇒ ΔADB ≅ ΔEDC
⇒ AB = EC [∵ corresponding parts of congruent triangles are equal]
Now in ΔAEC, we have
AC + EC > AE [∵ Sum of any two sides of a Δ is greater than the third]
⇒ AC + AB > 2 AD
[∵ AD =DE ∴ AE = AD + DE = 2AD and EC = AB]

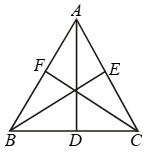
Example 13: In Fig. PQR is a triangle and S is any point in its interior, show that SQ + SR < PQ + PR.
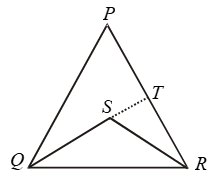
How Do You Prove Triangles Are Congruent 24
Solution:
Given: S is any point in the interior of ΔPQR.
To Prove: SQ + SR < PQ + PR
Construction: Produce QS to meet PR in T.
Proof: In PQT, we have
PQ + PT > QT [∵ Sum of the two sides of a Δ is greater than the third side]
⇒ PQ + PT > QS + ST …. (i)
[∵ QT = QS + ST]
In ΔRST, we have
ST + TR > SR …. (ii)
Adding (i) and (ii), we get
PQ + PT + ST + TR > SQ + ST + SR
⇒ PQ + (PT + TR) > SQ + SR
⇒ PQ + PR > SQ + SR ⇒ SQ + SR < PQ + PR.

Example 14: In ∆PQR S is any point on the side QR. Show that PQ + QR + RP > 2 PS.
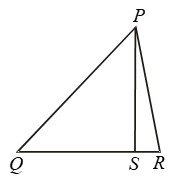
How Do You Prove Triangles Are Congruent 25
Solution:
In ΔPQS, we have
PQ + QS > PS … (i)
[∵ Sum of the two sides of a Δ is greater than the third side]
Similarly, in ΔPRS, we have
RP + RS > PS …. (ii)
Adding (i) and (ii), we get
(PQ + QS) + (RP + RS) > PS + PS
⇒ PQ + (QS + RS) + RP > 2 PS
⇒ PQ + QR + RP > 2 PS
[∵ QS + RS = QR]

Example 15: In Fig. T is a point on side QR of ∆PQR and S is a point such that RT = ST.
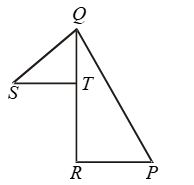
How Do You Prove Triangles Are Congruent 26
Prove that PQ + PR > QS.
Solution:
In ΔPQR, we have
PQ + PR > QR
⇒ PQ + PR > QT + RT [∵ QR = QT + RT]
⇒ PQ + PR > QT + ST …. (i)
[∵ RT = ST (Given)]
In ΔQST, we have
QT + ST > QS …. (ii)
From (i) and (ii), we get
PQ + PR > QS.

Example 16: Find ∠OBA in given figure
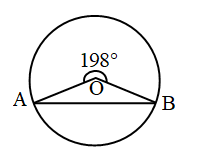
How Do You Prove Triangles Are Congruent 27
Solution:
∵ ∠AOB + 198° = 360°
∠AOB = 360° – 198° = 162°
and OA = OB = radius of circle
∠A = ∠B = x (let)
∴ x + x + 162° = 180° (a.s.p.)
2x + 18°
x = 9°
∴ ∠OBA = 9°.

How Do You Find The Angle Of An Isosceles Triangle

December 9, 2020December 9, 2020 by Veerendra

How Do You Find The Angle Of An Isosceles Triangle

find-angle-of-isosceles-triangle-1
Theorem: Angles opposite to equal sides of an isosceles triangle are equal.
How Do You Find The Angle Of An Isosceles Triangle 1
Given: In ∆ABC, AB = AC
To Prove: ∠B = ∠C
Construction: Draw AD, bisector of ∠A
∴ ∠1 = ∠2
Proof: In ∆ADB & ∆ADC
AD = AD (Common)
∠1 = ∠2 (by construction)
AB = AC
By SAS, ∆ADB ≅ ∆ADC
∴ ∠B = ∠C (c.p.c.t.) Proved.

Note: Other result: ∠ADB = ∠ADC (c.p.c.t.)
But ∠ADB + ∠ADC = 180° (linear pair)
∴ ∠ADB = ∠ADC = 90° ⇒ AD ⊥ BC
and BD = DC (c.p.c.t.) ⇒ AD is median
∴ we can say AD is perpendicular bisector of BC or we can say in isosceles ∆, median is angle bisector and perpendicular to base also.

Read More:

Angle Of An Isosceles Triangle Example Problems With Solutions

Example 1: Find ∠BAC of an isosceles triangle in which AB = AC and ∠B = 1/3 of right angle.
Solution:
Angle-Of-An-Isosceles-Triangle-Example-1

Example 2: In isosceles triangle DEF, DE = EF and ∠E = 70° then find other two angles.
Angle-Of-An-Isosceles-Triangle-Example-1
Solution:

Example 3: ∆ABC and ∆DBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see fig.). If AD is extended to intersect BC at P. Show that
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC.
Angle-Of-An-Isosceles-Triangle-Example-2
Solution:

Example 4: Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ∆PQR (see figure ). Show that:
(i) ∆ABM ≅ ∆PQN (ii) ∆ABC ≅ ∆PQR
Angle-Of-An-Isosceles-Triangle-Example-3
Solution:

Pythagoras Theorem

December 8, 2020December 8, 2020 by Veerendra

Pythagoras Theorem

Theorem 1: In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Given: A right-angled triangle ABC in which B = ∠90º.
To Prove: (Hypotenuse)² = (Base)² + (Perpendicular)².
i.e., AC² = AB² + BC²
Construction: From B draw BD ⊥ AC.
Pythagoras Theorem 1
Proof: In triangle ADB and ABC, we have
∠ADB = ∠ABC [Each equal to 90º]
and, ∠A = ∠A [Common]
So, by AA-similarity criterion, we have
∆ADB ~ ∆ABC
$\Rightarrow \frac{AD}{AB}=\frac{AB}{AC}$ [∵ In similar triangles corresponding sides are proportional]
⇒ AB² = AD × AC ….(i)
In triangles BDC and ABC, we have
∠CDB = ∠ABC [Each equal to 90º]
and, ∠C = ∠C [Common]
So, by AA-similarity criterion, we have
∆BDC ~ ∆ABC
$\Rightarrow \frac{DC}{BC}=\frac{BC}{AC}$ [∵ In similar triangles corresponding sides are proportional]
⇒ BC² = AC × DC ….(ii)
Adding equation (i) and (ii), we get
AB² + BC² = AD × AC + AC × DC
⇒ AB² + BC² = AC (AD + DC)
⇒ AB² + BC² = AC × AC
⇒ AC² = AB² + BC²
Hence, AC² = AB² + BC²
The converse of the above theorem is also true as proved below.

Read also:

Theorem 2: (Converse of Pythagoras Theorem).
In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the side is a right angle.
Given: A triangle ABC such that AC² = AB² + BC²
Pythagoras Theorem 2
Construction: Construct a triangle DEF such that DE = AB, EF = BC and ∠E = 90º,
Proof: In order to prove that B = ∠90º, it is sufficient to show that ∆ABC ~ ∆DEF.
For this we proceed as follows :
Since ∆DEF is a right angled triangle with right angle at E. Therefore, by Pythagoras theorem, we have
DF² = DE² + EF²
⇒ DF² = AB² + BC² [∵ DE = AB and EF = BC (By construction)]
⇒ DF² = AC² [∵ AB² + BC² = AC² (Given)]
⇒ DF = AC ….(i)
Thus, in ∆ABC and ∆DEF, we have
AB = DE, BC = EF [By construction]
and, AC = DF [From equation (i)]
∴ ∆ABC ~ ∆DEF
⇒ ∠B = ∠E = 90º
Hence, ∆ABC is a right triangle right angled at B.

Pythagoras Theorem With Examples

Example 1: Side of a triangle is given, determine it is a right triangle.
(2a – 1) cm, $2\sqrt { 2a } $ cm, and (2a + 1) cm
Sol. Let p = (2a – 1) cm, q = $2\sqrt { 2a } $ cm and r = (2a + 1) cm.
Then, (p² + q²) = (2a – 1)² cm² + (2 )² cm²
= {(4a² + 1– 4a) + 8a}cm²
= (4a² + 4a + 1)cm²
= (2a + 1)² cm² = r².
(p² + q²) = r².
Hence, the given triangle is right angled.

Example 2: A man goes 10 m due east and then 24 m due north. Find the distance from the starting point.
Sol. Let the initial position of the man be O and his final position be B. Since the man goes 10 m due east and then 24 m due north. Therefore, ∆AOB is a right triangle right-angled at A such that OA = 10 m and AB = 24 m.
Pythagoras Theorem 3
By Phythagoras theorem, we have
OB² = OA² + AB²
⇒ OB² = 10² + 24² = 100 + 576 = 676
⇒ OB = $\sqrt { 676 } $ = 26 m
Hence, the man is at a distance of 26 m from the starting point.

Example 3: Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops.
Sol.
Pythagoras Theorem 4
By Phythagoras theorem, we have
AC² = CE² + AE²
⇒ AC² = 15² + 20² = 225 + 400 = 625
⇒ AC = $\sqrt { 625 } $ = 25 m.

Example 4: In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that
AC² = AB² + BC² + 2BC × BD
Sol. Given: An obtuse triangle ABC, obtuse-angled at B and AD is perpendicular to CB produced.
To Prove: AC² = AB² + BC² + 2BC × BD
Proof: Since ∆ADB is a right triangle right angled at D. Therefore, by Pythagoras theorem, we have AB² = AD² + DB² ….(i)
Pythagoras Theorem 5
Again ∆ADC is a right triangle right angled at D.
Therefore, by Phythagoras theorem, we have
AC² = AD² + DC²
⇒ AC² = AD² + (DB + BC)²
⇒ AC² = AD² + DB² + BC² + 2BC • BD
⇒ AC² = AB² + BC² + 2BC • BD [Using (i)]
Hence, AC² = AB² + BC² + 2BC • BD

Example 5: In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that
AC² = AB² + BC² – 2BC × BD
Sol. Given: A ∆ABC in which ∠B is an acute angle and AD ⊥ BC.
To Prove: AC² = AB² + BC² – 2BC × BD.
Proof: Since ∆ADB is a right triangle right-angled at D. So, by Pythagoras theorem, we have
AB² = AD² + BD² ….(i)
Again ∆ADC is a right triangle right angled at D.
Pythagoras Theorem 6
So, by Pythagoras theorem, we have
AC² = AD² + DC²
⇒ AC² = AD² + (BC – BD)²
⇒ AC² = AD² + (BC² + BD² – 2BC • BD)
⇒ AC² = (AD² + BD²) + BC² – 2BC • BD
⇒ AC² = AB² + BC² – 2BC • BD [Using (i)]
Hence, AC² = AB² + BC² – 2BC • BD

Example 6: If ABC is an equilateral triangle of side a, prove that its altitude = $\frac { \sqrt { 3 } }{ 2 } a$.
Sol. ∆ABD is an equilateral triangle.
We are given that AB = BC = CA = a.
AD is the altitude, i.e., AD ⊥ BC.
Now, in right angled triangles ABD and ACD, we have
AB = AC (Given)
and AD = AD (Common side)
∆ABD ≅ ∆ACD (By RHS congruence)
⇒ BD = CD ⇒ BD = DC = $\frac { 1 }{ 2 }BC$ = $\frac { a }{ 2 }$
Pythagoras Theorem 7
From right triangle ABD.
AB² = AD² + BD²
$\Rightarrow {{a}^{2}}=A{{D}^{2}}+{{\left( \frac{a}{2} \right)}^{2}} $
$\Rightarrow A{{D}^{2}}={{a}^{2}}-\frac{{{a}^{2}}}{4}=\frac{3}{4}{{a}^{2}}$
$\Rightarrow AD=\frac{\sqrt{3}}{2}a $

Example 7: ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle.
Sol. Given that ∆ABC is right angled at A.
AC = 5 cm and AB = 12 cm
BC² = AC² + AB² = 25 + 144 = 169
BC = 13 cm
Join OA, OB, OC
Pythagoras Theorem 8
Let the radius of the inscribed circle be r
Area of ∆ABC = Area of ∆OAB + Area of ∆OBC + Area of ∆OCA
⇒ 1/2 × AB × AC
$=\frac{1}{2}\left( 12\text{ }\times \text{ }r \right)\text{ }+\frac{1}{2}\left( 13\text{ }\times \text{ }r \right)\text{ }+\frac{1}{2}\left( 5\text{ }\times \text{ }r \right)$
⇒ 12 × 5 = r × {12 + 13 + 5}
⇒ 60 = r × 30 ⇒ r = 2 cm

Example 7: ABCD is a rhombus. Prove that
AB² + BC² + CD² + DA² = AC² + BD²
Sol. Let the diagonals AC and BD of rhombus ABCD intersect at O.
Since the diagonals of a rhombus bisect each other at right angles.
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90º
and AO = CO, BO = OD.
Since ∆AOB is a right triangle right-angle at O.
Pythagoras Theorem 9
∴ AB² = OA² + OB²
$\Rightarrow A{{B}^{2}}={{\left( \frac{1}{2}AC \right)}^{2}}+{{\left( \frac{1}{2}BD \right)}^{2}}$ [∵ OA = OC and OB = OD]
⇒ 4AB² = AC² + BD² ….(i)
Similarly, we have
4BC² = AC² + BD² ….(ii)
4CD² = AC² + BD² ….(iii)
and, 4AD² = AC² + BD² ….(iv)
Adding all these results, we get
4(AB² + BC² + AD²) = 4(AC² + BD²)
⇒ AB² + BC² + AD² + DA² = AC² + BD²

Example 8: P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
(i) 4AQ² = 4AC² + BC²
(ii) 4BP² = 4BC² + AC²
(iii) (4AQ² + BP²) = 5AB²
Sol.
Pythagoras Theorem 10
(i) Since ∆AQC is a right triangle right-angled at C.
∴ AQ² = AC² + QC²
⇒ 4AQ² = 4AC² + 4QC²[Multiplying both sides by 4]
⇒ 4AQ² = 4AC² + (2QC)²
⇒ 4AQ² = 4AC² + BC² [∵ BC = 2QC]
(ii) Since ∆BPC is a right triangle right-angled at C.
∴ BP² = BC² + CP²
⇒ 4BP² = 4BC² + 4CP²[Multiplying both sides by 4]
⇒ 4BP² = 4BC² + (2CP)²
⇒ 4BP² = 4BC² + AC² [∵ AC = 2CP]
(iii) From (i) and (ii), we have
4AQ² = 4AC² + BC² and, 4BC² = 4BC² + AC²
∴ 4AQ² + 4BP² = (4AC² + BC²) + (4BC² + AC²)
⇒ 4(AQ² + BP²) = 5 (AC² + BC²)
⇒ 4(AQ² + BP²) = 5 AB²
[In ∆ABC, we have AB² = AC² + BC²]

Example 9: From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that :
(i) AF² + BD² + CE² = OA² + OB² + OC² – OD² – OE² – OF²
(ii) AF² + BD² + CE² = AE² + CD² + BF²
Sol.
Pythagoras Theorem 11
Let O be a point in the interior of ∆ABC and let OD ⊥ BC, OE ⊥ CA and OF ⊥ AB.
(i) In right triangles ∆OFA, ∆ODB and ∆OEC, we have
OA² = AF² + OF²
OB² = BD² + OD²
and, OC² = CE² + OE²
Adding all these results, we get
OA² + OB² + OC² = AF² + BD² + CE² + OF² + OD² + OE²
⇒ AF² + BD² + CE² = OA² + OB² + OC² – OD² – OE² – OF²
(ii) In right triangles ∆ODB and ∆ODC, we have
OB² = OD² + BD²
and, OC² = OD² + CD²
OB² – OC² = (OD² + BD²) – (OD² + CD²)
⇒ OB² – OC² = BD² – CD² ….(i)
Similarity, we have
OC² – OA² = CE² – AE² ….(ii)
and, OA² – OB² = AF² – BF² ….(iii)
Adding (i), (ii) and (iii), we get
(OB² – OC²) + (OC² – OA²) + (OA² – OB²)
= (BD² – CD²) + (CE² – AE²) + (AF² – BF²)
⇒ (BD² + CE² + AF²) – (AE² + CD² + BF²) = 0
⇒ AF² + BD² + CE² = AE² + CD² + BF²

Example 10: In a right triangle ABC right-angled at C, P and Q are the points on the sides CA and CB respectively, which divide these sides in the ratio 2 : 1. Prove that
(i) 9 AQ² = 9 AC² + 4 BC²
(ii) 9 BP² = 9 BC² + 4 AC²
(iii) 9 (AQ² + BP²) = 13 AB²
Sol. It is given that P divides CA in the ratio 2 : 1. Therefore,
$CP=\frac { 2 }{ 3 }AC$ ….(i)
Also, Q divides CB in the ratio 2 : 1.
∴ $QC=\frac { 2 }{ 3 }BC$ ….(ii)
Pythagoras Theorem 12
(i) Applying pythagoras theorem in right-angled triangle ACQ, we have
AQ² = QC² + AC²
⇒ AQ² = $\frac { 4 }{ 9 }$ BC² + AC² [Using (ii)]
⇒ 9 AQ² = 4 BC² + 9 AC² ….(iii)
(ii) Applying pythagoras theorem in right triangle BCP, we have
BP² = BC² + CP²
⇒ BP² = BC² + AC² [Using (i)]
⇒ 9 BP² = 9 BC² + 4 AC² ….(iv)
(iii) Adding (iii) and (iv), we get
9 (AQ² + BP²) = 13 (BC² + AC²)
⇒ 9 (AQ² + BP²) = 13 AB² [∵ BC² = AC² + AB²]

Example 11: In a ∆ABC, AD ⊥ BC and AD² = BC × CD. Prove ∆ABC is a right triangle.
Sol.
Pythagoras Theorem 13
In right triangles ADB and ADC, we have
AB² = AD² + BD² ….(i)
and, AC² = AD² + DC² ….(ii)
Adding (i) and (ii), we get
AB² + AC² = 2 AD² × BD² + DC²
⇒ AB² + AC² = 2BD × CD + BD² + DC² [∵ AD² = BD × CD (Given)]
⇒ AB² + AC² = (BD + CD)² = BC²
Thus, in ∆ABC, we have
AB² = AC² + BC²
Hence, ∆ABC, is a right triangle right-angled at A.

Example 12: The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that 2AB² = 2AC² + BC².
Sol. We have,
Pythagoras Theorem 14
DB = 3CD
BC = BD + DC
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that
2AC2 + BC2.
We have,
DB = 3CD
∴ BC = BD + DC
⇒ BC = 3 CD + CD
⇒ BD = 4 CD ⇒ CD = $\frac { 1 }{ 4 }$ BC
∴ CD = $\frac { 1 }{ 4 }$ BC and BD = 3CD = $\frac { 1 }{ 4 }$ BC ….(i)
Since ∆ABD is a right triangle right-angled at D.
∴ AB² = AD² + BD² ….(ii)
Similarly, ∆ACD is a right triangle right angled at D.
∴ AC² = AD² + CD² ….(iii)
Subtracting equation (iii) from equation (ii) we get
AB² – AC² = BD² – CD²
⇒ AB² – AC² = ${{\left( \frac{3}{4}BC \right)}^{2}}-{{\left( \frac{1}{4}BC \right)}^{2}}$ $\left[ From\ (i)\ CD=\frac{1}{4}BC,\ BD=\frac{3}{4}BC \right]$
⇒ AB² – AC² = $\frac { 9 }{ 16 }$ BC² – $\frac { 1 }{ 16 }$ BC²
⇒ AB² – AC² = $\frac { 1 }{ 2 }$ BC²
⇒ 2(AB² – AC²) = BC²
⇒ 2AB² = 2AC² + BC².

Example 13: ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
(ii) $\frac{1}{{{p}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}$
Sol. (i) Let CD ⊥ AB. Then, CD = p.
Pythagoras Theorem 14
∴ Area of ∆ABC = $\frac { 1 }{ 2 }$ (Base × Height)
⇒ Area of ∆ABC = $\frac { 1 }{ 2 }$ (AB × CD) = $\frac { 1 }{ 2 }$ cp
Also,
Area of ∆ABC = $\frac { 1 }{ 2 }$ (BC × AC) = $\frac { 1 }{ 2 }$ ab
∴ $\frac { 1 }{ 2 }$ cp = $\frac { 1 }{ 2 }$ ab
⇒ cp = ab
(ii) Since ∆ABC is right triangle right-angled at C.
∴ AB² = BC² + AC²
⇒ c² = a² + b²
$\Rightarrow {{\left( \frac{ab}{p} \right)}^{2}}={{a}^{2}}+{{b}^{2}} $ $\left[ \because \ cp\,=\,ab\ \ \therefore c=\frac{ab}{p} \right]$
$\Rightarrow \frac{{{a}^{2}}{{b}^{2}}}{{{p}^{2}}}={{a}^{2}}+{{b}^{2}} $
$\Rightarrow \frac{1}{{{p}^{2}}}=\frac{{{a}^{2}}+{{b}^{2}}}{{{a}^{2}}{{b}^{2}}}\Rightarrow \frac{1}{{{p}^{2}}}=\frac{1}{{{b}^{2}}}+\frac{1}{{{a}^{2}}} $
$\Rightarrow \frac{1}{{{p}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}} $

Criteria For Congruent Triangles

December 8, 2020December 8, 2020 by Veerendra

Criteria For Congruent Triangles

https://www.youtube.com/watch?v=QkU4FZN8MY0

Congruent triangles are triangles that have the same size and shape. This means that the corresponding sides are equal and the corresponding angles are equal.

Congruent Triangles do not have to be in the same orientation or position. They only have to be identical in size and shape.

SSS (Side Side Side) Congruence Criteria (Condition):
Two triangles are congruent, if three sides of one triangle are equal to the corresponding three sides of the other triangle.

∴ By SSS criteria ∆ABC ∆EDF
∴ ∠A = ∠E, ∠B = ∠D, ∠C = ∠F (c.p.c.t.)
ASA (Angle Side Angle) Congruence Criteria (Condition):
Two triangles are congruent, if two angles and the included side of one is equal to the corresponding angles and side of the other.

∴ By ASA criteria ∆ABC ≅ ∆DEF
∴ ∠A = ∠D, AB = DE, AC = DF (c.p.c.t.)
AAS (Angle Angle Side) Congruence Criteria (Condition):

∴ By AAS, ∆ABC ≅ ∆FDE
∴ ∠C = ∠E, AB = FD, AC = FE (c.p.c.t.)
SAS (Side Angle Side) Congruence Criteria (Condition):
When two sides and the included angle of one triangle is equal to the corresponding sides and the included angle of another triangle, the two triangles are congruent. This, condition of congruence is known as side-angle-side congruence. In short we write SAS condition.

By SAS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, AC = QR (c.p.c.t.)
RHS (Right Hypotenuse Side) Congruence Criteria (Condition):
Two right triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.

∴ By RHS, ∆ABC ≅ ∆QPR
∴ ∠A = ∠Q, ∠C = ∠R, BC = PR (c.p.c.t.)

Example 1:
Criteria For Congruent Triangles 6

Example 2:
Criteria For Congruent Triangles 7

Example 3:
Criteria For Congruent Triangles 8

Example 4:
Criteria For Congruent Triangles 9

Read More:

Theorem 1: If two angles and the included side of one triangle are equal to two angles and the included side of other triangle, then both triangles are congruent.
Proof:
Given: ∆ABC and ∆DEF in which
∠ABC = ∠DEF, ∠ACB = ∠DFE and BC = EF.
Criteria For Congruent Triangles 10
To Prove: ∆ABC ≅ ∆DEF.
Proof:
Case I:
Let AC = DF.
In this case, AC = DF, BC = EF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria)
Case II:
If possible, let AC ≠ DF.
Then, construct D’ F = AC. Join D’ E.
Now, in ∆ABC and ∆D’EF, we have AC = D’F, BC = EF and ∠C = ∠F.
∴ ∆ABC ∆D’EF (SAS-criteria)
∴ ∠ABC = ∠D’EF (c.p.c.t)
But, ∠ABC = ∠DEF (given)
∴ ∠D’EF = ∠DEF.
This is possible only when D and D’ coincide.
∴ ∆ABC ≅ ∆DEF.

Theorem 2: Two right-angled triangles are congruent if one side and the hypotenuse of the one are respectively equal to the corresponding side and the hypotenuse of the other. (i.e. RHS)
Given: Two right-angled triangles ∆ABC & ∆DEF in which ∠B = ∠E = 90°, BC = EF and AC = DF.
To Prove: ∆ABC ≅ ∆DEF.
Construction: Produce DE to G such that
GE = AB. Join GF.
Criteria For Congruent Triangles 11
Proof: In ∆ABC and ∆GEF, we have:
AB = GE (construction),
BC = EF (given),
∠B = ∠FEG = 90°
⇒ ∆ABC ∆GEF (SAS-criteria)
⇒ ∠A = ∠G and AC = GF (c.p.c.t.)
Now, AC = GF and AC = DF ⇒GF = DF
⇒ ∠G = ∠D ⇒ ∠A = ∠D [∵ ∠G = ∠A]
Now, ∠A = ∠D, ∠B = ∠E ⇒ 3rd ∠C = 3rd ∠F.
Thus, in ∆ABC and ∆DEF, we have:
BC = EF, AC = DF and ∠C = ∠F.
∴ ∆ABC ≅ ∆DEF (SAS-criteria).

Criteria For Congruent Triangles Example Problems With Solutions

Example 1: Prove that diagonal of a parallelogram divides it into two congruent triangles.
Solution: Let ABCD is a parallelogram and AC is a diagonal.
Criteria For Congruent Triangles 12
(By SSS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
BC = AD (opp. sides of ||gm)
AC = AC (common)
∴ By SSS, ∆ABC ≅ ∆CDA proved
{other results : ∠1 = ∠2, ∠3 = ∠4, ∠B = ∠D (c.p.c.t.)}
(By ASA): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
AC = AC (common)
∠3 = ∠4 (alternate)
∴ By ASA, ∆ABC ≅ ∆CDA
{other results: ∠B = ∠D, AB = CD, BC = AD (c.p.c.t.)}
(By AAS): In ∆ABC and ∆ADC
∠1 = ∠2 (alternate)
∠3 = ∠4 (alternate)
BC = AD (opp. sides)
∴ ∆ABC ≅ ∆CDA
{other results : AB = CD, ∠B = ∠D, AC = AC (c.p.c.t.)}
(By SAS): In ∆ABC and ∆ADC
AB = CD (opp. sides of ||gm)
∠1 = ∠2 (alternate)
AC = AC (common)
∴ ∆ABC ≅ ∆CDA
{other results: ∠3 = ∠4, BC = AD, ∠B = ∠D (c.p.c.t.)
We can not use ‘RHS’ for this proof.
Note: ASS or SSA criteria for congruency is not valid.

Example 2: In Fig. it is given that AB = CF, EF = BD and ∠AFE = ∠DBC. Prove that ∆AFE ∆CBD.
Criteria For Congruent Triangles 13
Solution: We have, AB = CF
⇒ AB + BF = CF + BF
⇒ AF = CB …. (i)
In ∆s AFE and CBD, we have
AF = CB [From (i)]
∠AFE = ∠DBC [Given]
and EF = BD [Given]
So, by SAS criterion of congruence, we have
∆AFE ≅ ∆CBD

Example 3: In Fig. X and Y are two points on equal sides AB and AC of a ∆ABC such that AX = AY. Prove that XC = YB.
Criteria For Congruent Triangles 14
Solution: In ∆s AXC and AYB, we have
AX = AY [Given]
∠A = ∠A [Common angle]
AC = AB [Given]
So, by SAS criterion of congruene
∆AXC ≅ ∆AYB
⇒ XC = YB (c.p.c.t.)

Example 4: In Fig. PQRS is a quadrilateral and T and U are respectively points on PS and RS such PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
Criteria For Congruent Triangles 15
Solution: We have,
∠PQT = ∠RQU
and, ∠TQS = ∠UQS
∴ ∠PQT + ∠TQS = ∠RQU + ∠UQS
⇒ ∠PQS = ∠RQS …. (i)
Thus, in triangles PQS and RQS, we have
PQ = RQ [Given]
∠PQS = ∠RQS [From (i)]
and, QS = QS [Common side]
Therefore, by SAS congruence criterion, we have
∆PQS ≅ ∆RQS
⇒ ∠QPS = ∠QRS (c.p.c.t.)
⇒ ∠QPT = ∠QRU …. (ii)
Now, consider triangles QPT and QRS. In these two triangles, we have
QP = QR [Given]
∠PQT = ∠RQU [Given]
∠QPT = ∠QRU [From (ii)]
Therefore, by ASA congruence criterion, we get
∆QPT ≅ ∆QRU
⇒ QT = QU.

Example 5: In Fig. PS = QR and ∠SPQ = ∠RQP.
Criteria For Congruent Triangles 16
Prove that PR = QS and ∠QPR = ∠PQS.
Solution: In ∆SPQ and ∆RQP, we have
PS = QR [Given]
∠SPQ = ∠RQP [Given]
PQ = PQ [Common]
Therefore, by SAS criterion of congruence, we have
∆SPQ ∆RQP ⇒ SQ = RP and
∠QPR = ∠PQS

Example 6: ∆ABC is an isosceles triangle with AB = AC. Side BA is produced to D such that
AB = AD. Prove that ∠BCD is a right angle.
Solution: Given : A ∆ABC such that AB = AC. Side BA is produced to D such that AB = AD.
Criteria For Congruent Triangles 17
Construction : Join CD.
To prove : ∠BCD = 90º
Proof : In ∆ABC, we have AB = AC
⇒ ∠ACB = ∠ABC …(i) [∵ Angles opp. to equal sides are equal]
Now, AB = AD [Given]
∴ AD = AC [∴ AB = AC]
Thus, in ∆ADC, we have
AD = AC
⇒ ∠ACD = ∠ADC …(ii)
[∵ Angles opp. to equal sides are equal]
Adding (i) and (ii), we get
∠ACB + ∠ACD = ∠ABC + ∠ADC
⇒ ∠BCD = ∠ABC + ∠BDC
[∵ ∠ADC = ∠BDC, ∠ABC = ∠DBC]
⇒ ∠BCD + ∠BCD = ∠DBC + ∠BCD + ∠BDC
[adding ∠BCD on both sides ]
⇒ 2 ∠BCD = 180º
[∵ Sum of the angles of a ∆ is 180º]
Hence, ∠BCD is a right angle.

Example 7: In Fig. AC = BC, ∠DCA = ∠ECB and ∠DBC = ∠EAC.
Criteria For Congruent Triangles 18
Prove that triangles DBC and EAC are congruent, and hence DC = EC.
Solution: We have,
∠DCA = ∠ECB
⇒ ∠DCA + ∠ECD = ∠ECB + ∠ECD
⇒ ∠ECA = ∠DCB …. (i)
Now, in ∆s DBC and EAC, we have
∠DCB = ∠ECA [From (i)]
BC = AC [Given]
and ∠DBC = ∠EAC [Given]
So, by ASA criterion of congruence
∆DBC ≅ ∠EAS
⇒ DC = EC (c.p.c.t.)

Example 8: If the altitudes from two vertices of a triangle to the opposite sides are equal, prove that the triangle is isosceles.
Solution: Given: A ∆ABC in which altitudes BE and CF from B and C respectively on AC and AB are equal.
Criteria For Congruent Triangles 19
To prove: ∆ABC is isoceles i.e. AB = AC
Proof: In ∆s ABC and ACF, we have
∠AEB = ∠AFC [Each equal to 90º]
∠BAE = ∠CAF [Common angle]
and, BE = CF [Given]
So, by AAS criterion of congurence, we have
∆ABE ≅ ∆ACF
⇒ AB = AC [∵ Corresopnding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.

Example 9: In ∆ABC, AB = AC and the bisectors of angles B and C intersect at point O. Prove that BO = CO and the ray AO is the bisector of angle BAC.
Solution: In ∆ABC, we have
AB = AC
Criteria For Congruent Triangles 20
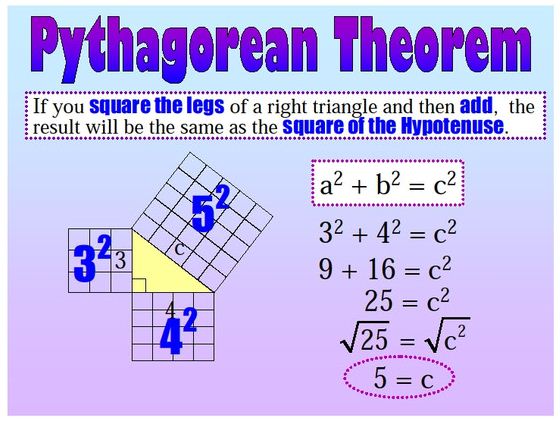
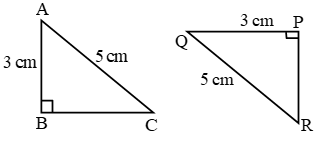
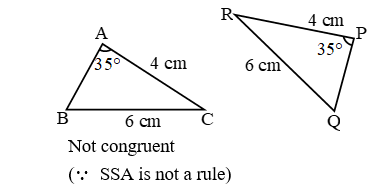
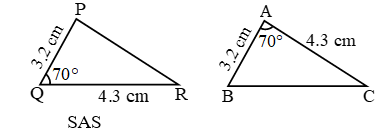
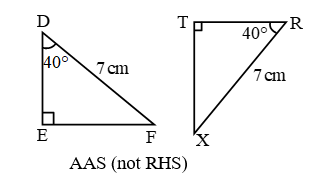
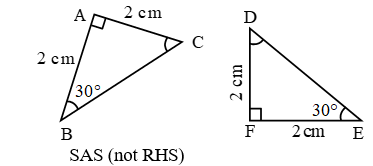
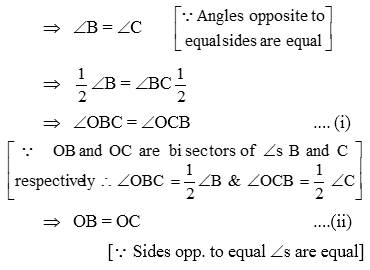
criteria-for-congruent-triangles-example-9-1
Now, in ∆ABO and ∆ACO, we have
AB = AC [Given]
∠OBC = ∠OCB [From (i)]
OB = OC [From (ii)]
So, by SAS criterion of congruence
∆ABO ≅ ∆ACO
⇒ ∠BAO = ∠CAO
[∵ Corresponding parts of congruent triangles are equal]
⇒ AO is the bisector of ∠BAC.

Example 10: In Fig. BM and DN are both perpendiculars to the segments AC and BM = DN.
Criteria For Congruent Triangles 21
Prove that AC bisects BD.
Solution: In ∆s BMR and DNR, we have
∠BMR = ∠DNR
[Each equal to 90º ∵ BM ⊥ AC and DN ⊥ AC]
∠BRM = ∠DRN [Vert. opp. angles]
and, BM = DN [Given]
So, by AAS criterion of congruence
∆BMR ≅ ∆DNR
⇒ BR = DR
[∵ Corresponding parts of congruent triangles are equal]
⇒ R is the mid-point of BD.
Hence, AC bisects BD.

Example 11: In Fig. BD and CE are two altitudes of a ∆ABC such that BD = CE.
Criteria For Congruent Triangles 22
Prove that ∆ABC is isolceles.
Solution: In ∆ABD and ∆ACE, we have
∠ADB = ∠AEC = 90º [Given]
∠BAD = ∠CAE [Common]
and, BD = CE [Given]
So, by AAS congruence criterion, we have
∆ABD ≅ ∆ACE
⇒ AB = AC [∵ Corresponding parts of congruent triangles are equal]
Hence, ∆ABC is isosceles.

Example 12: If two isosceles triangles have a common base, the line joining their vertices bisects them at right angles.
Solution: Given: Two isosceles triangles ABC and DBC having the common base BC such that AB = AC and DB = DC.
To prove: AD (or AD produced) bisects BC at right angle.
Criteria For Congruent Triangles 23
Proof : In ∆s ABD and ACD, we have
AB = AC [Given]
BD = CD [Given]
AD = AD [Common side]
So, by SSS criterion of congruence
∆ABD ≅ ∆ACD
⇒ ∠1 = ∠2 …. (i)
[∵ Corresponding parts of congruent triangles are equal]
Now, in ∆s ABE and ACE, we have
AB = AC [Given]
∠1 = ∠2 [From (i)]
and, AE = AE [Commoni side]
So, by SAS criterion of congruence,
∆ABE ≅ ∆ACE
⇒ BE = CE
[∵ Corresponding parts of congruent triangles are equal]
and, ∠3 = ∠4
But, ∠3 + ∠4 = 180º
[∵ Sum of the angles of a linear pair is 180º]
⇒ 2 ∠3 = 180º [∵ ∠3 = ∠4]
⇒ ∠3 = 90º
∴ ∠3 = ∠4 = 90º
Hence, AD bisects BC at right angles.

Example 13: AD, BE and CF, the altitudes of ∆ABC are equal. Prove that ∆ABC is an equilateral triangle
Solution: In right triangles BCE and BFC, we have
Hyp. BC = Hyp. BC
BE = CF [Given]
So, by RHS criterion of congruence,
Criteria For Congruent Triangles 24
∆BCE ∆BFC.
⇒ ∠B = ∠C [∵ Corresponding parts of congruent triangles are equal]
⇒ AC = AB …. (i)
[∵ Sides opposite to equal angles are equal]
Similarly, ∆ABD ≅ ∆ABE
⇒ ∠B =∠A
[Corresponding parts of congruent triangles are equal]
⇒ AC = BC …. (ii)
[Sides opposite to equal angles are equal]
From (i) and (ii), we get
AB = BC = AC
Hence, ∆ABC is an equilateral triangle.

Example 14: In Fig. AD = BC and BD = CA.
Criteria For Congruent Triangles 25
Prove that ∠ADB = ∠BCA and
∠DAB = ∠CBA.
Solution: In triangles ABD and ABC, we have
AD = BC [Given]
BD = CA [Given]
and AB = AB [Common]
So, by SSS congruence criterion, we have
∆ABD ∠CBA ⇒ ∠DAB = ∠ABC
[∵ Corresponding parts of congruent triangles are equal]
⇒ ∠DAB = ∠CBA

Example 15: Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see figure). Show that (i) ∆AOB ≅ ∆DOC (ii) O is also the mid point of BC.
Solution: (i) Consider ∆AOB and ∆DOC
∠ABO = ∠DCO
(Alternate angles as AB || CD and BC is the transversal)
Criteria For Congruent Triangles 26
∠AOB = ∠DOC (Vertically opposite angles)
OA = OD (Given)
Therefore, ∆AOB ≅ ∆DOC (AAS rule)
(ii) OB = OC (c.p.c.t.)
So, O is the mid-point of BC.

Example 16: In quadrilateral ABCD, AC = AD and AB bisects ∠A. Show that ∆ABC ∆ABD. What can you say about BC and BD ?
Criteria For Congruent Triangles 27
Solution: In ∆ABC & ∆ABD
AB = AB (common)
∠1 = ∠2 {∵ AB is bisector of ∠A}
AC = AD (Given)
∴ By SAS, ∆ABC ≅ ∆ABD Proved
also BC = BD (c.p.c.t.)

Example 17: AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.
Criteria For Congruent Triangles 28
Solution: To show CD bisect AB i.e. AO = OB
∴ in ∆OAD and ∆OBC
∠O = ∠O (vertically opposite angles)
∠A = ∠B = 90° (Given)
AD = BC (Given)
∴ By AAS, ∆OAD ≅ ∆OBC
∴ OA = OB (c.p.c.t.)
∴ CD, bisects AB. Proved

Example 18: Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that
Criteria For Congruent Triangles 29
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
Solution: (i) In ∆APB and ∆AQB
∠P = ∠Q = 90° (Given)
∠PAB = ∠QAB (Given that ‘l’ bisect ∠A)
AB = AB (Common)
∴ By AAS, ∆APB ≅ ∆AQB. Proved
(ii) BP = BQ (c.p.c.t.) Proved.

Example 19: In given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
Criteria For Congruent Triangles 30
Solution: In ∆ABC and ∆ADE
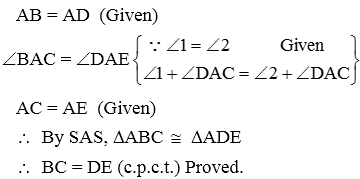
criteria-for-congruent-triangles-example-19

Example 20: In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that:
Criteria For Congruent Triangles 31
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB
(iv) CM = AB
Solution: (i) In ∆AMC and ∆BMD
AM = MB (M is mid point of AB)
∠1 = ∠2 (vertically opposite angles)
CM = MD (given)
∴ By SAS, ∆AMC ≅ ∆MBD Proved.
(ii) ∠ACM = ∠MDB (c.p.c.t. of (i))
These are alternate angles
∴ DB || AC
So ∠DBC + ∠ACB = 180°
(Cointerior angles)
⇒ ∠DBC + 90° = 180°
⇒ ∠DBC = 90° Proved.
(iii) In ∆DBC & ∆ACB
BC = BC ( common)
∠DBC = ∠ACB = 90°
DB = AC (c.p.c.t. of part (i))
∴ By SAS, ∆DBC ≅ ∆ACB. Proved
(iv) DC = AB (c.p.c.t. of part (iii))
But CM = DC (given)
∴ CM = AB Proved.

What are the Different Types of Triangles

December 7, 2020December 6, 2020 by Veerendra

Classification of Triangles

A triangle is a polygon with three sides. It has three sides and three vertices. There are seven types of triangles. The sum of the angles of a triangle is 180°.

Triangles Types can be classified in two ways:

By their sides
By their angles

what are the six types of triangles?

Six Various Types of Triangles are Isosceles, Equilateral, Obtuse, Acute and Scalene.

Classification of Triangles by Sides

Scalene Triangle:
A triangle that has no side of equal length is called a scalene triangle.
What are the Different Types of Triangles 1 In figure, PQ ≠ QR ≠ PR, so ΔPQR is a scalene triangle.

Isosceles Triangle:
A triangle that has two sides of equal length, is called an isosceles triangle.
What are the Different Types of Triangles 2 In figure, AB = AC, so ΔABC is an isosceles triangle.

Equilateral Triangle:
A triangle which has all the three sides equal in length is called an equilateral triangle.
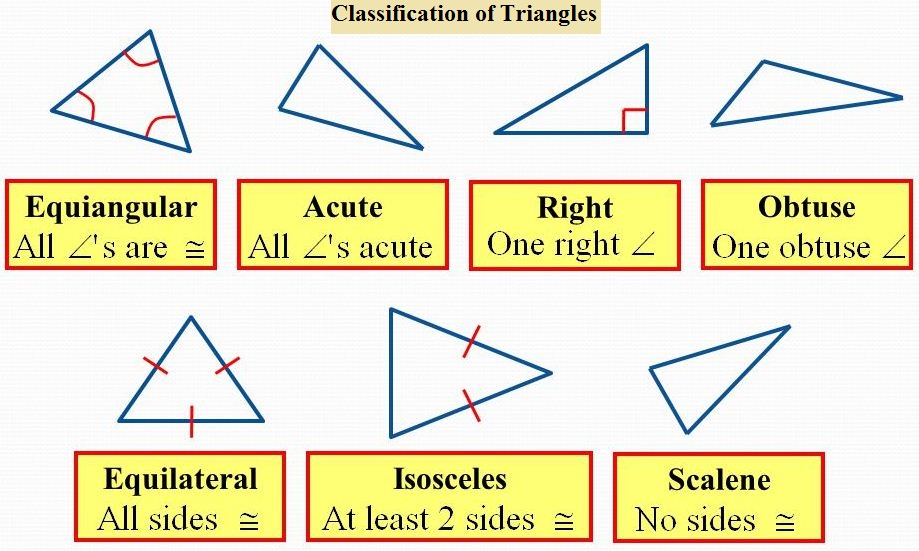
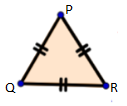What are the Different Types of Triangles 3 In figure, PQ = QR = PR, so ΔPQR is an equilateral triangle.

Classification of Triangles by Angles

Acute-angled Triangle:
A triangle whose all angles are acute (less than 90°), is called an acute-angled triangle or simply an acute triangle.
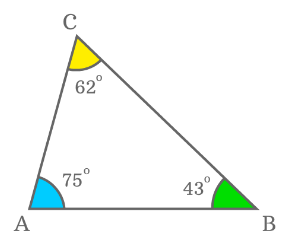What are the Different Types of Triangles 4 In figure, ∠A, ∠B, and ∠C are all less than 90°, hence ΔABC is an acute-angled triangle.

Right-angled Triangle:
A triangle whose one of the angles is a right angle, i.e., 90°, is called a right-angled triangle or simply right triangle.
What are the Different Types of Triangles 6 In figure, ∠B = 90°, hence ΔABC is a right triangle.

Obtuse-angled Triangle:
A triangle whose one angle is obtuse, is called an obtuse-angled triangle or simply obtuse triangle.
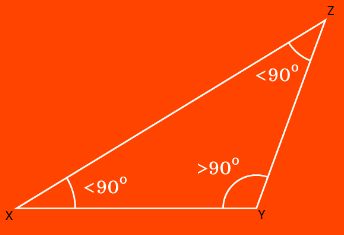What are the Different Types of Triangles 5 In figure, ∠Y is obtuse, hence ΔXYZ is an obtuse-angled triangle or simply obtuse triangle.

Equiangular Triangle:
When all the three angles of a triangle are equal, then it is known as an equiangular triangle.
An equiangular triangle is also known as equilateral triangle because all the three sides are equal.
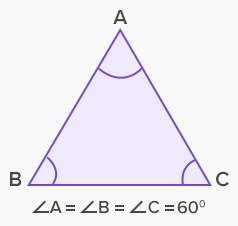What are the Different Types of Triangles 7 In figure, ∠A = ∠B = ∠C = 60°and AB = BC = AC, hence ΔABC is an equiangular triangle.

Example 1: One of the equal angles of an isosceles triangle is 50°. Find its third angle.
Solution: Let third angle = x
∴ x + 50° + 50° = 180°
(Angle sum property of a triangle)
or, x + 100° = 180°
or, x = 180° – 100°
= 80°
∴ Third angle = 80°

Example 2: Each ofthe two equal angles of a triangle is four times the third angle. Find all the angles of the triangle.
Solution: Let the smaller angle = x
∴ other two angles = 4x and 4x
Thus, x + 4x + 4x = 180°
(Angle sum property of a triangle) or, 9x = 180°
∴ 4x = 4 x 20°
= 80°
Thus, the angles of the triangle are 20°, 80°, and 80°.

Read More: