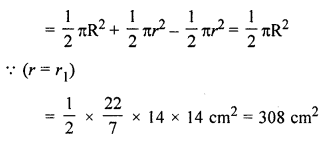ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 16 Perimeter and Area Check Your Progress
Question 1.
A 3 m wide path runs outside and around a rectangular park of length 125 m and breadth 65 m. Find the area of the path.
Solution:
Length of rectangular park (l) = 125 m
and breadth (b) = 65 m
Width of path around it = 3 m
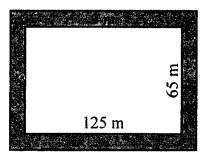
Outer length (L) = 125 + 2 × 3 = 125 + 6 = 131 m
and breadth = 65 + 2 × 3 = 65 + 6 = 71 m
Area of path = L × B – l × b
= 131 × 71 – 125 × 65
= 9301 – 8125 = 1176 m2
Question 2.
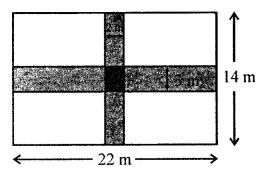
In the given figure, all adjacent line segments are at right angles. Find:
(i) the area of the shaded region
(ii) the area of the unshaded region.
Solution:
In the given figure,
Length (l) = 22 m
and breadth (b) = 14 m
Width of length wire region = 3 m
and breadth wire = 2 m
Area of shaded portion = 22 × 3 + 14 × 2 – 3 × 2 m2
= 66 + 28 – 6
= 88 m2
Total area = l × b = 22 × 14 = 308 m2
Area of unshaded region = 308 – 88 = 220 m2
Question 3.
Find the area of a triangle whose:
(i) base = 2 m, height = 1.5 m
(ii) base = 3.4 m and height = 90 cm
Solution:
(i) Base of a triangle (b) = 2 m
Height (h) = 1.5 m
Area = \(\frac { 1 }{ 2 }\) × b × h
= \(\frac { 1 }{ 2 }\) × 2 × 1.5 = 1.5 m2
(ii) Base of the triangle (b) = 3.4 m
and height (h) = 90 cm = \(\frac { 90 }{ 100 }\) = \(\frac { 9 }{ 10 }\) m
Area = \(\frac { 1 }{ 2 }\) × b × h
= \(\frac { 1 }{ 2 }\) × 3.4 × \(\frac { 9 }{ 10 }\)
= \(\frac { 30.6 }{ 20 }\) = 1.53 m2
Question 4.
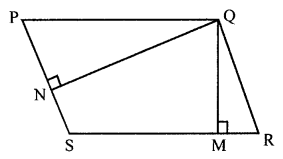
In the given figure, PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm, PS = 8 cm and QM = 7.6 cm, find:
(i) the area of the parallelogram PQRS
(ii) the length of QN.
Solution:
In the given figure,
PQRS is a parallelogram in which QM ⊥ SR and QN ⊥ PQ
SR = 12 cm, PS = 8 cm, QM = 7.6 cm
(i) Area of ||gm ABCD = b × h
= SR × QM
= 12 × 7.6 cm2
= 91.2 cm2
Base PS = 8 cm
Area of ||gm = 91.2 cm2
Heigh QN = \(\frac { Area }{ Base }\) = \(\frac { 91.2 }{ 8 }\) = 11.4 cm
Question 5.
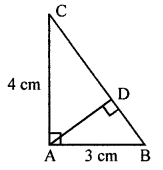
From the given figure, find
(i) the area of ΔABC
(ii) length of BC
(iii) the length of altitude from A to BC.
Solution:
In the given figure,
ABC is a right angled triangle in which
AB = 3 cm , AC = 4 cm
AD ⊥ BC
(i) Area ΔABC = \(\frac { 1 }{ 2 }\) × Base × Height
= \(\frac { 1 }{ 2 }\) × 3 × 4 = 6 cm2
(ii) BC2 = AB2 + AC2 (Pythagoras Theorem)
= 32 + 42 = 9 + 16 = 25 = (5)2
BC = 5 cm
(iii) Now length of altitude AD
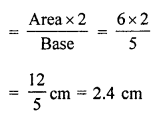
Question 6.
In the given figure, the area of the right-angled triangle is 54 cm2. If one of its legs is 12 cm long, find its perimeter.
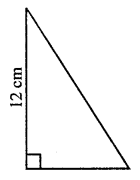
Solution:
In the given figure,
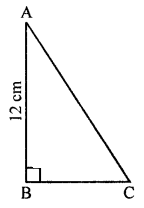
Area of right-angled triangle = 54 cm2
Length of one leg AB = 12 cm
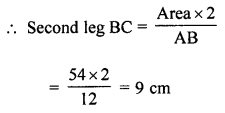
Now AC2 = AB2 + BC2 (Pythagoras Theorem)
= 122 + 92 = 144 + 81 = 225 = (15)2
AC = 15 cm
Now perimeter = AB + BC + AC = 12 + 9 + 15 = 36 cm
Question 7.
If the area of a circle is 78.5 cm2, find its circumference. (Take π = 3.14)
Solution:
Area of a circle = 78.5 cm2
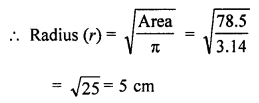
Circumference = 2πr = 2 × 3.14 × 5 = 31.4 cm
Question 8.
Find the circumference of the circle whose area is 16 times the area of the circle with diameter 7 cm.
Solution:
Diameter of first circle = 7 cm
Radius (r) = \(\frac { 7 }{ 2 }\) cm


Question 9.
From square cardboard, a circle of the biggest area was cut out. If the area of the circle is 154 cm2, calculate the original area of the cardboard.
Solution:
From square cardboard, the biggest circle is cut out
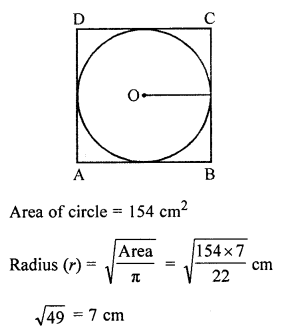
Side of square = diameter of the circle = 2 × 7 = 14 cm
Area of square cardboard = (Side)2 = (14)2 = 196 cm2
Question 10.
A road 3.5 m wide surrounds a circular park whose circumference is 88 m. Find the cost of paving the road at the rate of ₹ 60 per square meter.
Solution:
Circumference of a circular park = 88 m

Width of road surounded it = 3.5 m
Outer radius (R) = 14 + 3.5 = 17.5 m
Area of road = πR2 – πr2 = π(R2 – r2)
= \(\frac { 1 }{ 2 }\) × (17.52 – 142)
= \(\frac { 1 }{ 2 }\) × 31.5 × 3.5
= 346.5 m2
Cost of paving the road = ₹ 60 per m2
Total cost = ₹ 60 × 346.5 = ₹ 20790
Question 11.
In the given figure, ABCD is a square of side 14 cm. Find the area of the shaded region.
Take π = \(\frac { 22 }{ 7 }\)
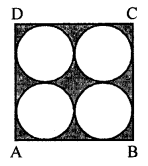
Solution:
In the given figure, ABCD is a square whose side is 14 cm.
Area of square = (Side)2 = (14)2 cm2 = 14 × 14 = 196 cm2
Radius of each circle in it = \(\frac { 7 }{ 2 }\) cm
Area of 4 circles = 4 × πr2
= 4 × \(\frac { 22 }{ 7 }\) × \(\frac { 7 }{ 2 }\) × \(\frac { 7 }{ 2 }\)
= 154 cm2
Area of shaded portion =196 – 154 = 42 cm2
Question 12.
The boundary of a shaded region in the given figure consists of three semicircles, the smaller being equal. If the diameter of the larger one is 28 cm, find
(i) the length of the boundary
(ii) the area of the shaded region.
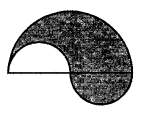
Solution:
In the given figure,
There are a bigger semicircle and two small semicircles
Diameter of bigger semicircle = 28 cm
Radius (R) = \(\frac { 28 }{ 2 }\) = 14 cm
and radius of each of smaller semicircles = \(\frac { 14 }{ 2 }\) = 7 cm
Now the area of shaded portion
= Area of bigger semicircle + Area of one smaller on semicircle
– Area of another smaller semicircle
Both small semicircles have the same area