Selina Concise Mathematics Class 10 ICSE Solutions Circles

Selina Concise Mathematics Class 10 ICSE Solutions Circles

Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 17 Circles

Circles Exercise 17A – Selina Concise Mathematics Class 10 ICSE Solutions

Circles Class 10 Question 1.
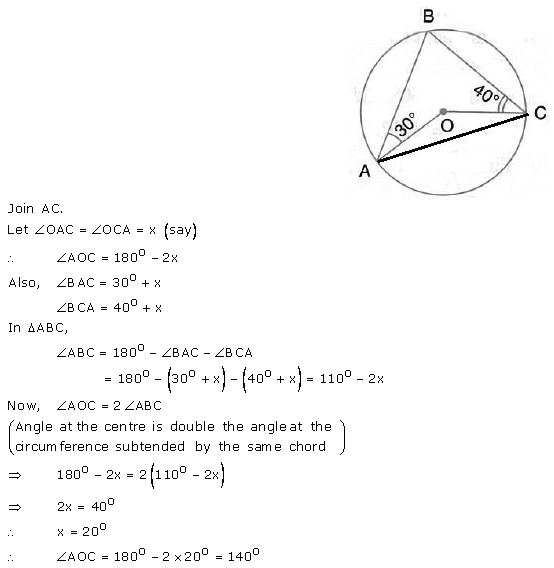
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. Find ∠AOC. Show your steps of working.

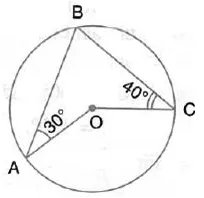
Solution:

Question 2.
In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
(i) Prove that AC is a diameter of the circle.
(ii) Find ∠ACB.

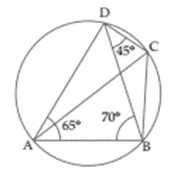
Solution:

Question 3.
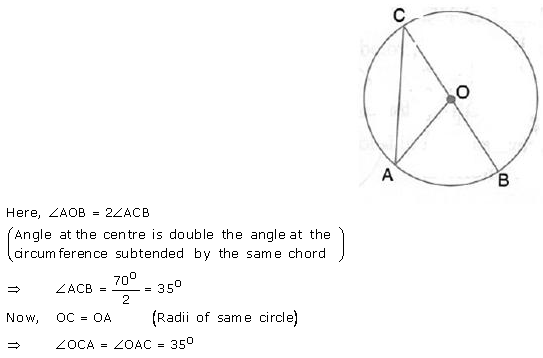
Given O is the centre of the circle and ∠AOB = 70°. Calculate the value of:
(i) ∠ OCA,
(ii) ∠OAC.

Solution:

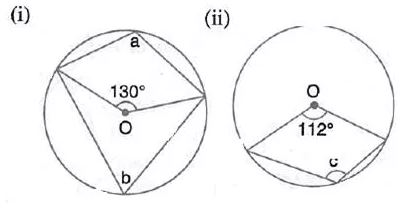
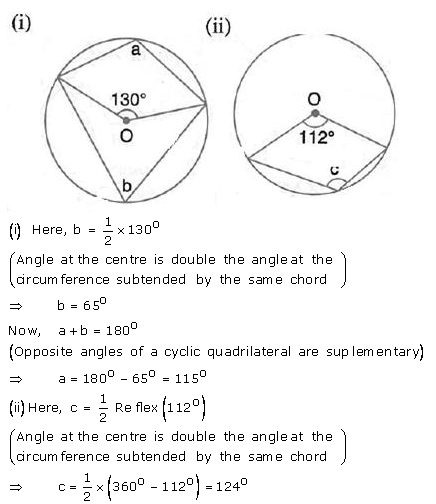
Question 4.
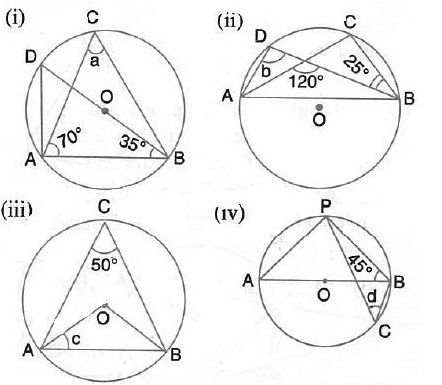
In each of the following figures, O is the centre of the circle. Find the values of a, b, and c.

Solution:

Question 5.
In each of the following figures, O is the centre of the circle. Find the value of a, b, c and d.

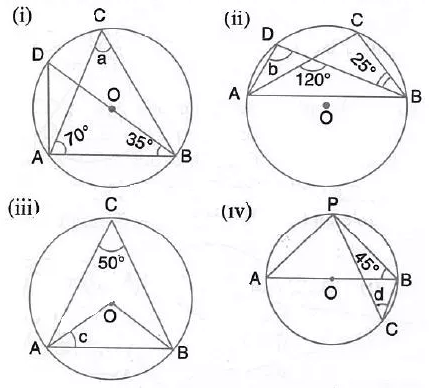
Solution:

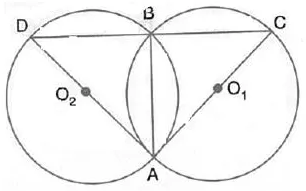
Question 6.
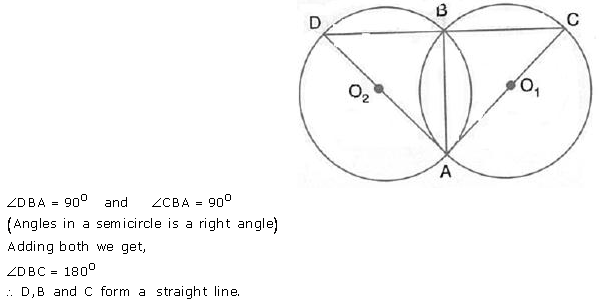
In the figure, AB is common chord of the two circles. If AC and AD are diameters; prove that D, B and C are in a straight line. O₁ and O₂ are the centres of two circles.

Solution:

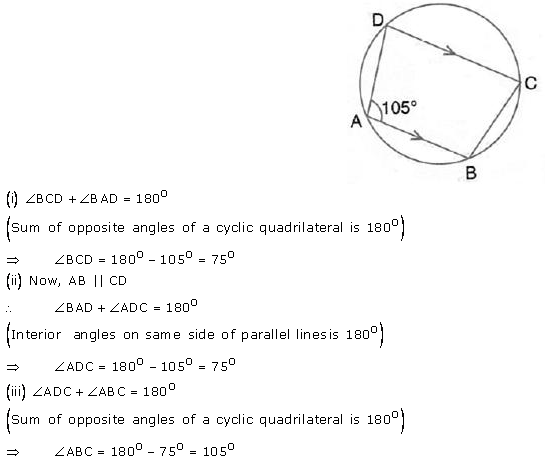
Question 7.
In the figure given beow, find :
(i) ∠ BCD,
(ii) ∠ ADC,
(iii) ∠ ABC.

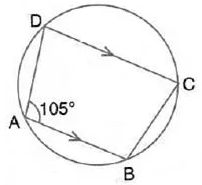
Show steps of your workng.
Solution:

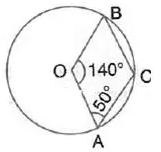
Question 8.
In the given figure, O is centre of the circle. If ∠ AOB = 140° and ∠ OAC = 50°; find :
(i) ∠ ACB,
(ii) ∠ OBC,
(iii) ∠ OAB,
(iv) ∠CBA

Solution:

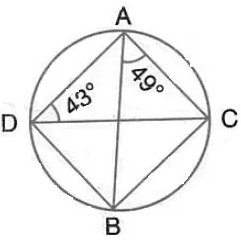
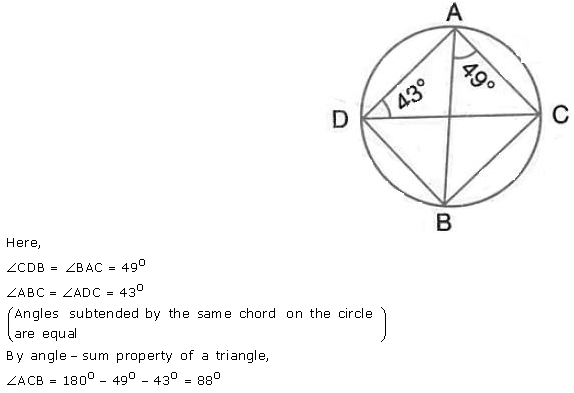
Question 9.
Calculate :
(i) ∠ CDB,
(ii) ∠ ABC,
(iii) ∠ ACB.

Solution:

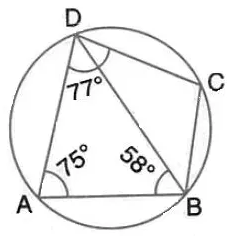
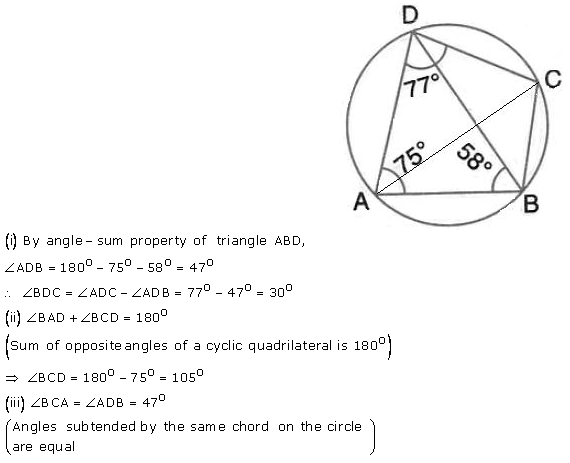
Question 10.
In the figure given below, ABCD is a eyclic quadrilateral in which ∠ BAD = 75°; ∠ ABD = 58° and ∠ADC = 77°. Find:
(i) ∠ BDC,
(ii) ∠ BCD,
(iii) ∠ BCA.

Solution:

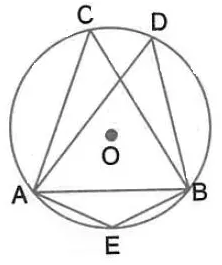
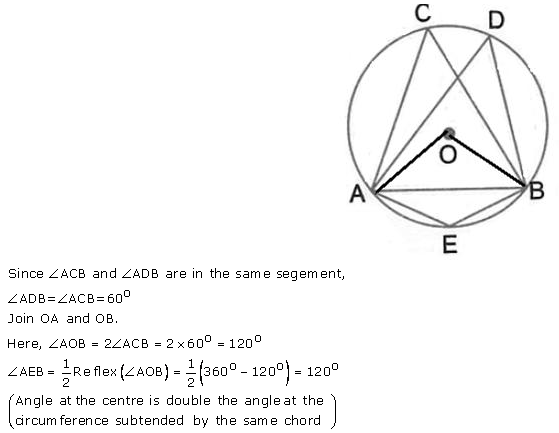
Question 11.
In the following figure, O is centre of the circle and ∆ ABC is equilateral. Find :
(i) ∠ ADB
(ii) ∠ AEB

Solution:

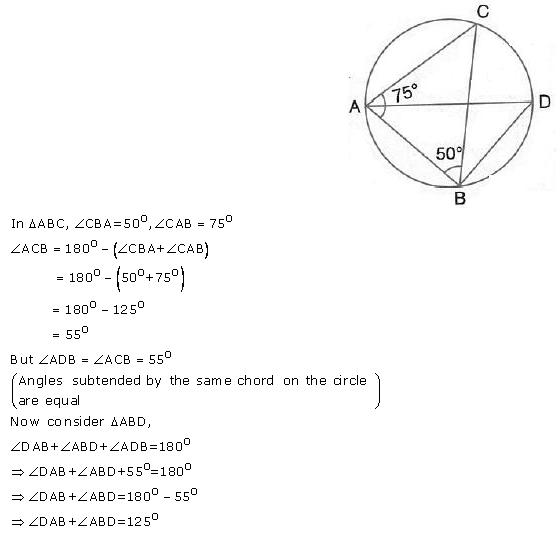
Question 12.
Given—∠ CAB = 75° and ∠ CBA = 50°. Find the value of ∠ DAB + ∠ ABD

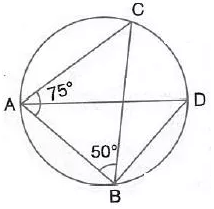
Solution:

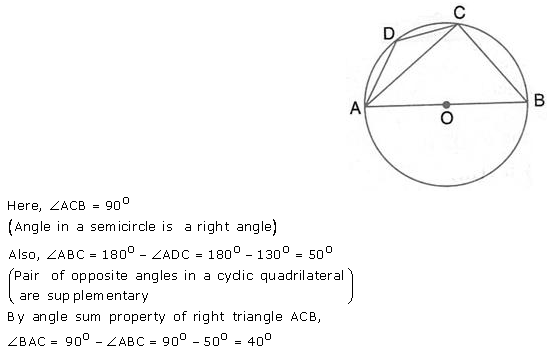
Question 13.
ABCD is a cyclic quadrilateral in a circle with centre O.
If ∠ ADC = 130°; find ∠ BAC.

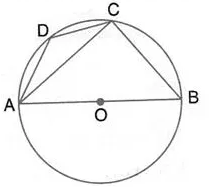
Solution:

Question 14.
In the figure given below, AOB is a diameter of the circle and ∠ AOC = 110°. Find ∠ BDC.

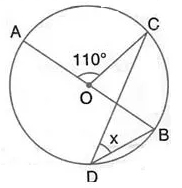
Solution:

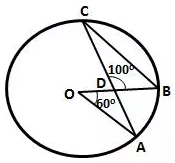
Question 15.
In the following figure, O is centre of the circle,
∠ AOB = 60° and ∠ BDC = 100°.
Find ∠ OBC.

Solution:

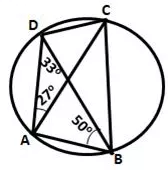
Question 16.
ABCD is a cyclic quadrilateral in which ∠ DAC = 27°; ∠ DBA = 50° and ∠ ADB = 33°.
Calculate :
(i) ∠ DBC,
(ii) ∠ DCB,
(iii) ∠ CAB.

Solution:

Question 17.
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°. Find the number of degrees in:
(i) ∠DCE;
(ii) ∠ABC.

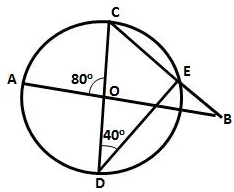
Solution:

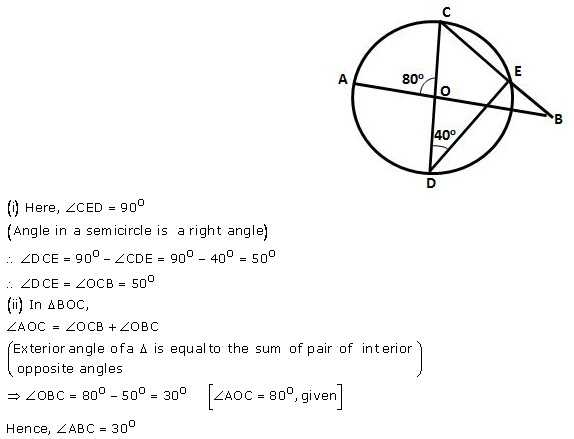
Question 17 (old).
In the figure given below, AB is diameter of the circle whose centre is O. Given that:
∠ ECD = ∠ EDC = 32°.

Show that ∠ COF = ∠ CEF.
Solution:

Question 18.
In the figure given below, AC is a diameter of a circle, whose centre is O. A circle is described on AO as diameter. AE, a chord of the larger circle, intersects the smaller circle at B. Prove that AB = BE.

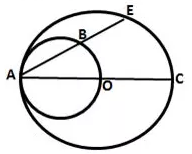
Solution:

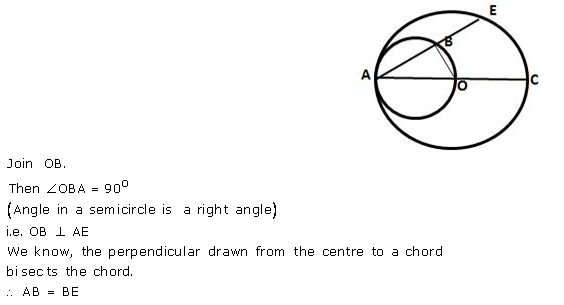
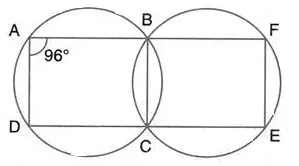
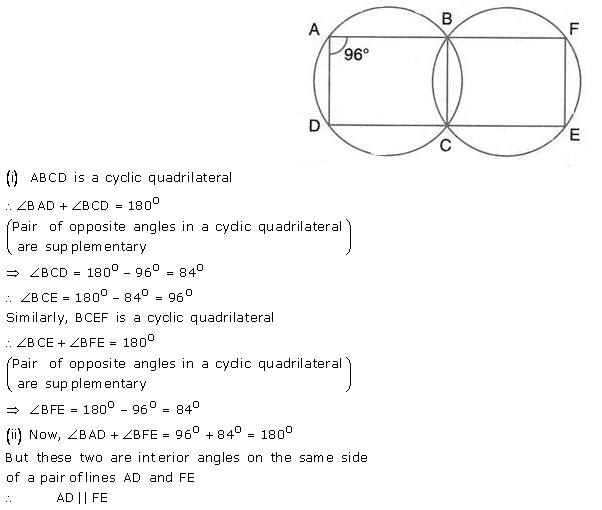
Question 19.
In the following figure,
(i) if ∠BAD = 96°, find BCD and
(ii) Prove that AD is parallel to FE.

Solution:

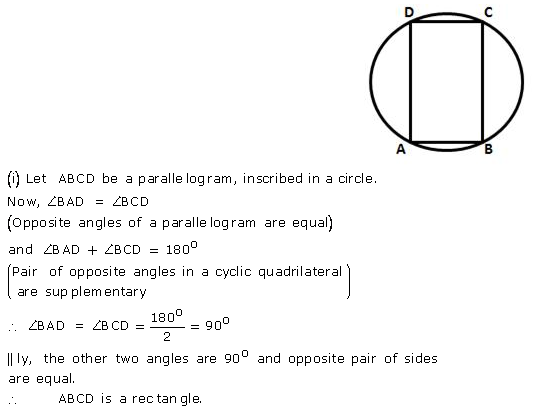
Question 20.
Prove that:
(i) the parallelogram, inscribed in a circle, is a rectangle.
(ii) the rhombus, inscribed in a circle, is a square.
Solution:

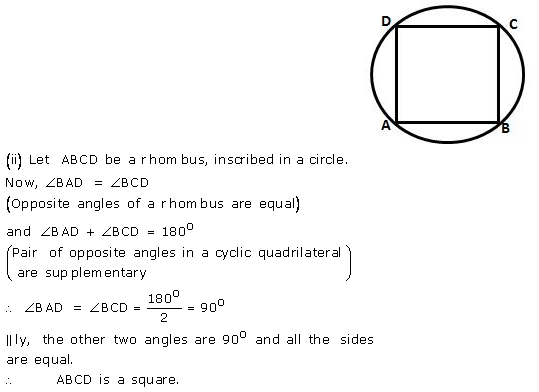
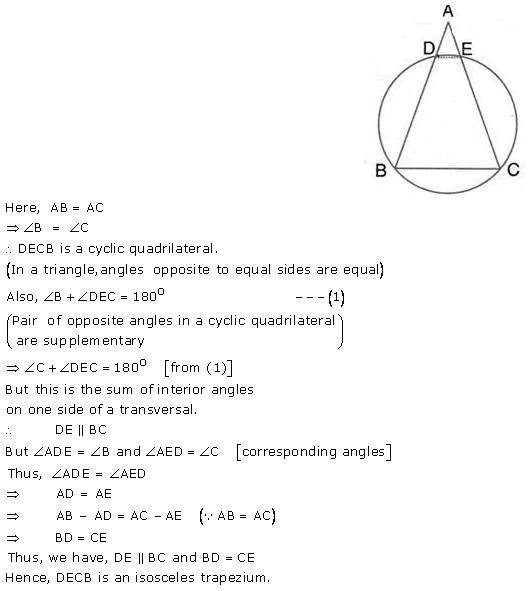
Question 21.
In the following figure, AB = AC. Prove that DECB is an isosceles trapezium.

Solution:

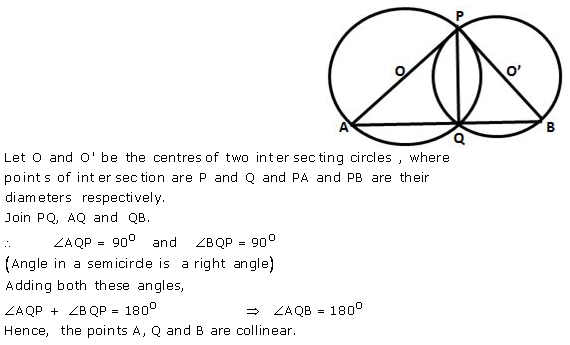
Question 22.
Two circles intersect at P and Q. Through P diameters PA and PB of the two circles are drawn. Show that the points A, Q and B are collinear.
Solution:

Question 23.
The figure given below, shows a circle with centre O. Given: ∠ AOC = a and ∠ ABC = b.
(i) Find the relationship between a and b
(ii) Find the measure of angle OAB, if OABC is a parallelogram.

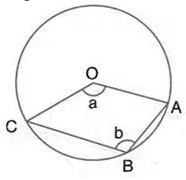
Solution:

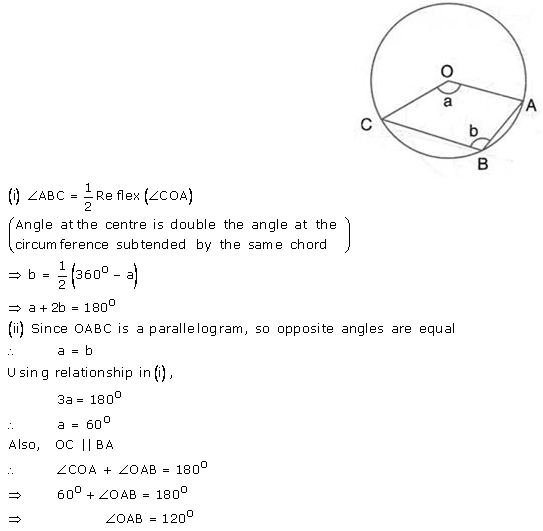
Question 24.
Two chords AB and CD intersect at P inside the circle. Prove that the sum of the angles subtended by the arcs AC and BD as the centre O is equal to twice the angle APC.
Solution:

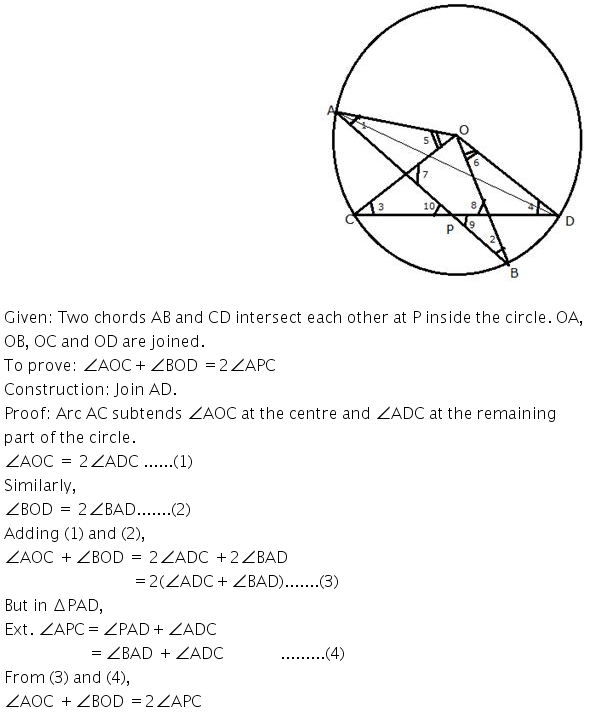
Question 24 (old).
ABCD is a quadrilateral inscribed in a circle having ∠A = 60°; O is the centre of the circle. Show that: ∠OBD + ∠ODB = ∠CBD + ∠CDB
Solution:

Question 25.
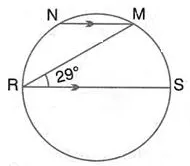
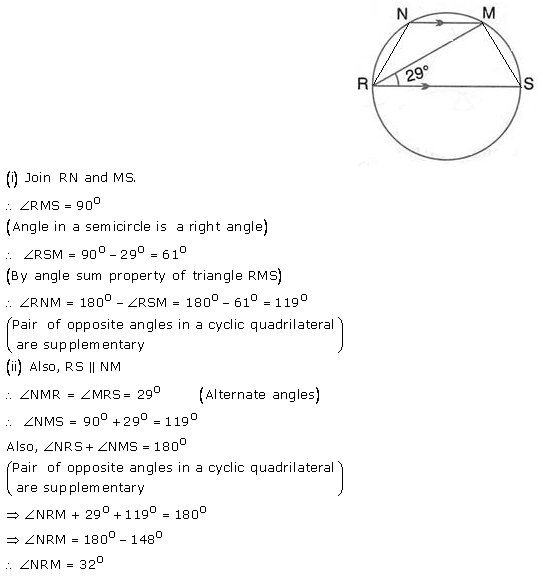
In the figure given RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°
Calculate:
(i) ∠RNM;
(ii) ∠NRM.

Solution:

Question 26.
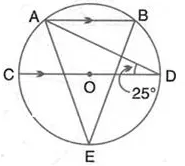
In the figure given alongside, AB || CD and O is the centre of the circle. If ∠ ADC = 25°; find the angle AEB. Give reasons in support of your answer.

Solution:

Question 27.
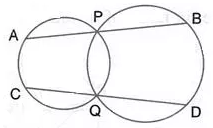
Two circles intersect at P and Q. Through P, a straight line APB is drawn to meet the circles in A and B. Through Q, a straight line is drawn to meet the circles at Cand D. Prove that AC is parallel to BD.

Solution:

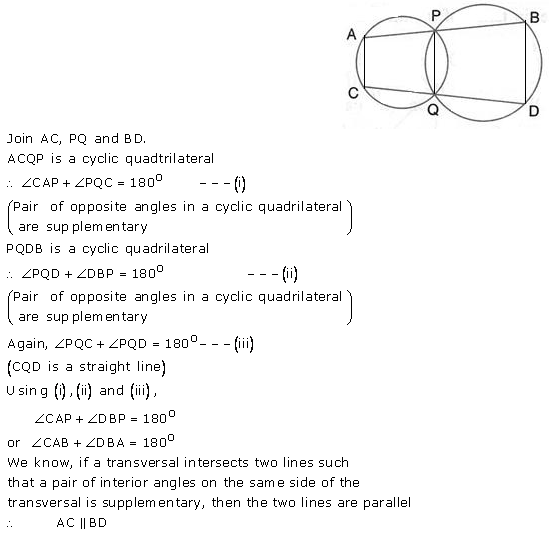
Question 28.
ABCD is a cyclic quadrilateral in which AB and DC on being produced, meet at P such that PA = PD. Prove that AD is parallel to BC.
Solution:

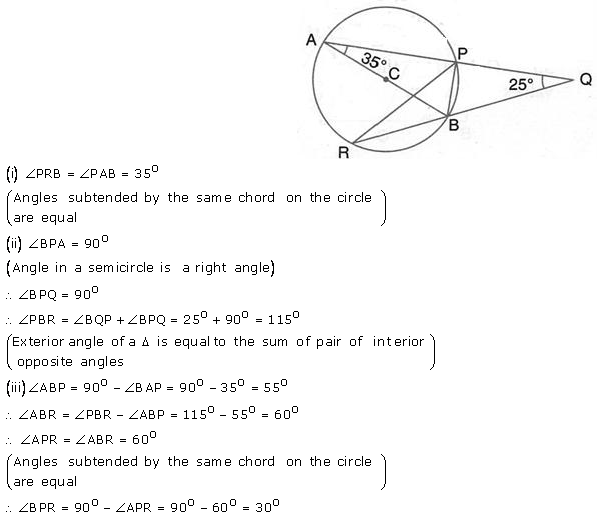
Question 29.
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find:
(i) ∠PRB
(ii) ∠PBR
(iii) ∠BPR.

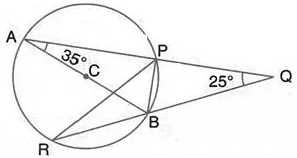
Solution:

Question 30.
In the given figure, SP is the bisector of angle RPT and PQRS is a cyclic quadrilateral. Prove that: SQ = SR.

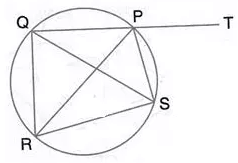
Solution:

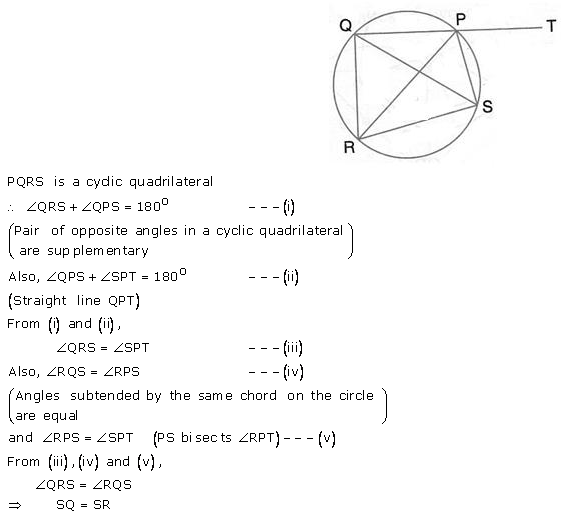
Question 31.
In the figure, O is the centre of the circle, ∠AOE = 150°, DAO = 51°. Calculate the sizes of the angles CEB and OCE.

Solution:

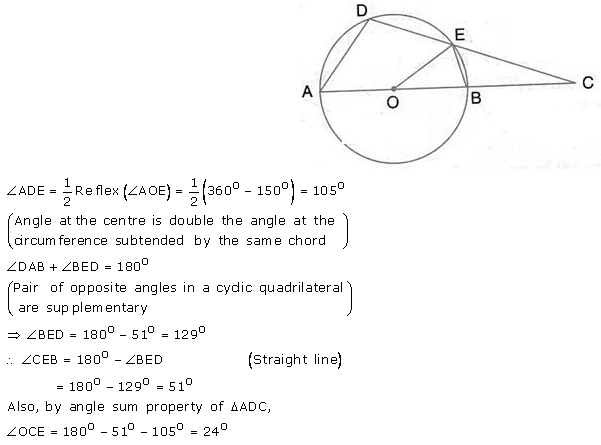
Question 32.
In the figure, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x.

Solution:

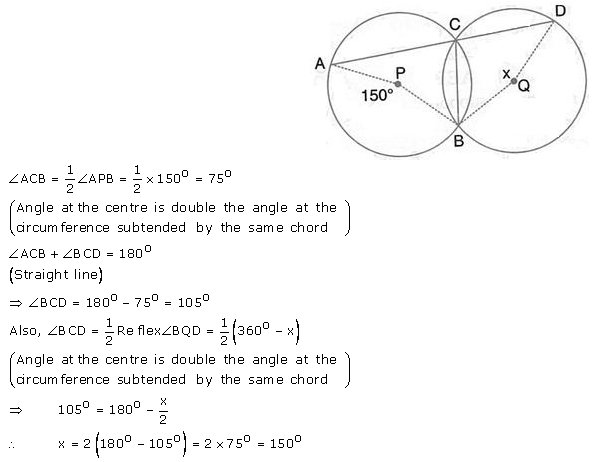
Question 33.
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°. Calculate, in terms of a°, the value of:
(i) obtuse ∠AOB
(ii) ∠ACB
(iii) ∠ADB.
Give reasons for your answers clearly.

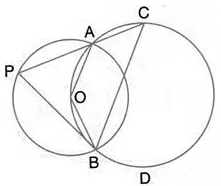
Solution:

Question 34.
In the given figure, O is the centre of the circle and ∠ ABC = 55°. Calculate the values of x and y.

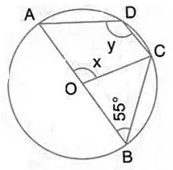
Solution:

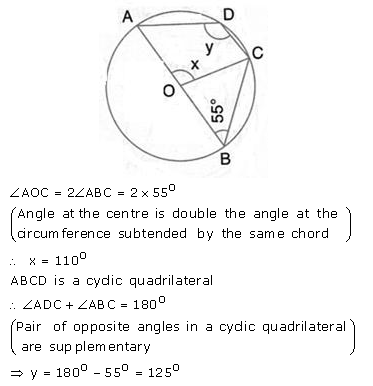
Question 35.
In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that ∠BCD = 2∠ABE

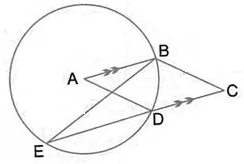
Solution:

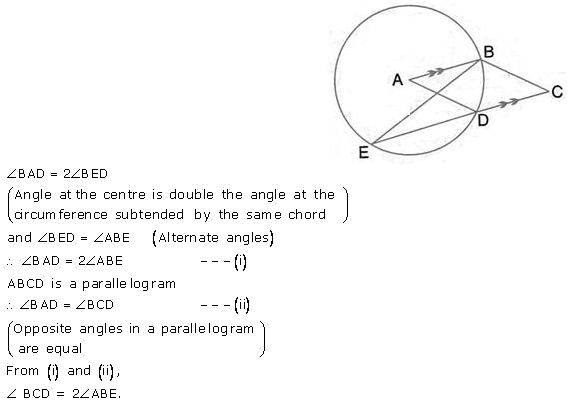
Question 36.
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED = 65°; calculate:
(i) ∠ DAB,
(ii) ∠BDC.

Solution:

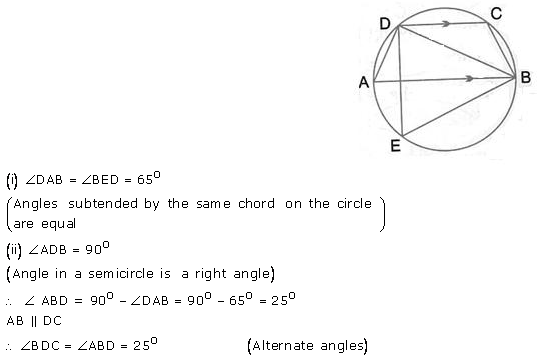
Question 37.
∠ In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠ EAB = 63°; calculate:
(i) ∠EBA,
(ii) BCD.

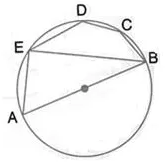
Solution:

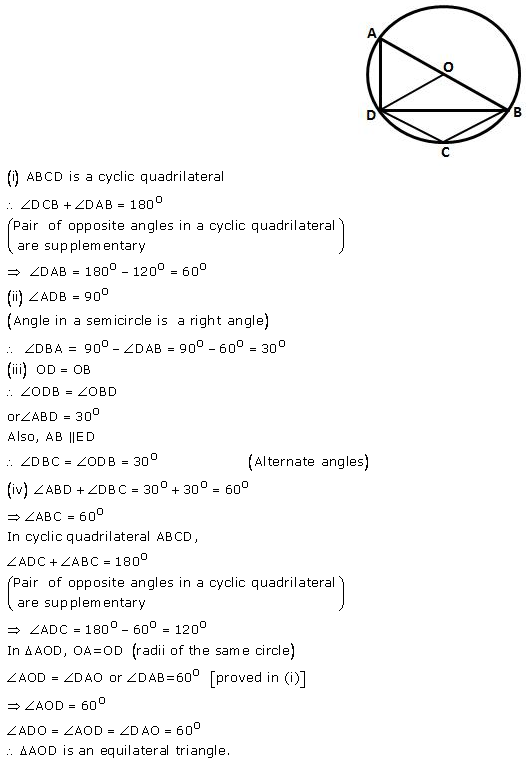
Question 38.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°; calculate:
(i) ∠ DAB,
(ii) ∠ DBA,
(iii) ∠ DBC,
(iv) ∠ ADC.
Also, show that the ∆AOD is an equilateral triangle.

Solution:

Question 39.
In the given figure, I is the incentre of the ∆ ABC. Bl when produced meets the circumcirle of ∆ ABC at D. Given ∠BAC = 55° and ∠ ACB = 65°, calculate:
(i) ∠DCA,
(ii) ∠ DAC,
(iii) ∠DCI,
(iv) ∠AIC.

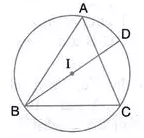
Solution:

Question 40.
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that:
(i) ∠ABC = 2 ∠APQ
(ii) ∠ACB = 2 ∠APR
(iii) ∠QPR = 90° – \(\frac{1}{2}\)BAC

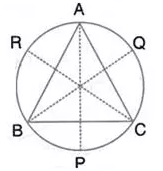
Solution:

Question 40 (old).
The sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E; the sides DA and CB are produced to meet at F. If ∠BEC = 42° and ∠BAD = 98°; calculate:
(i) ∠AFB,
(ii) ∠ADC.

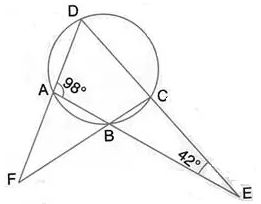
Solution:

Question 41.
Calculate the angles x, y and z if: \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)

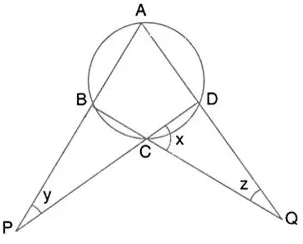
Solution:

Question 42.
In the given figure, AB = AC = CD and ∠ADC = 38°. Calculate:
(i) Angle ABC
(ii) Angle BEC.

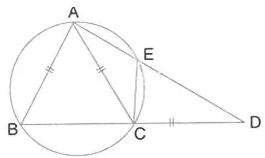
Solution:

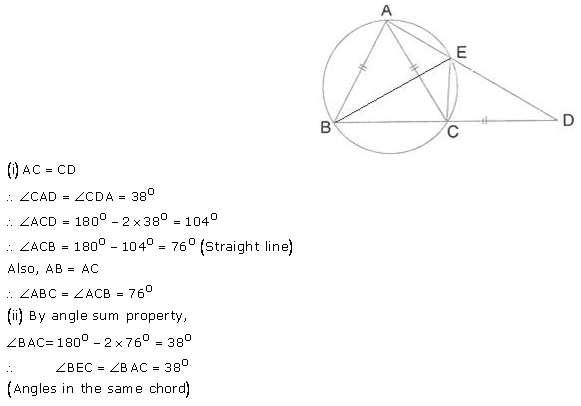
Question 43.
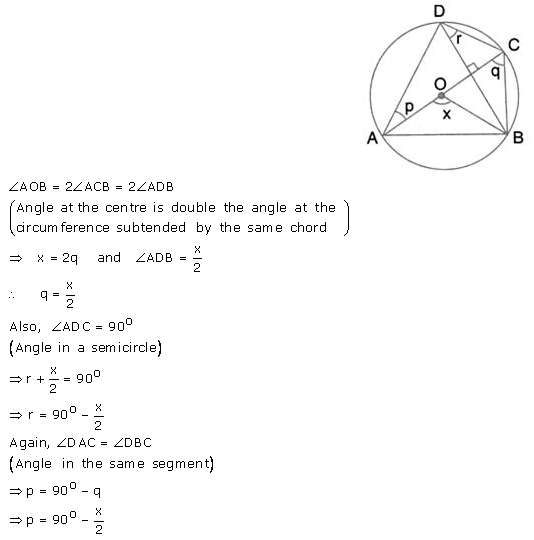
In the given figure, AC is the diameter of circle, centre O. Chord BD is perpendicular to AC. Write down the angles p, and r in terms of x.

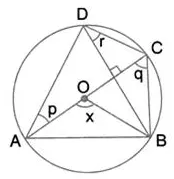
Solution:

Question 44.
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80° and angle ACE = 10°. Calculate:
(i) Angle BEC;
(ii) Angle BCD;
(iii) Angle CED.

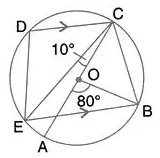
Solution:

Question 45.
In the given figure, AE is the diameter of circle. Write down the numerical value of ∠ABC + ∠CDE. Give reasons for your answer.

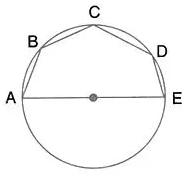
Solution:

Question 46.
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠CBE = 64°, calculate ∠DEC.

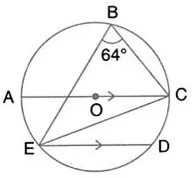
Solution:

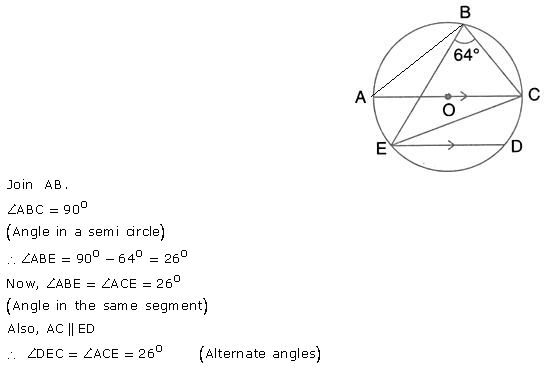
Question 47.
Use the given figure to find
(i) ∠BAD
(ii) ∠DQB.

Solution:

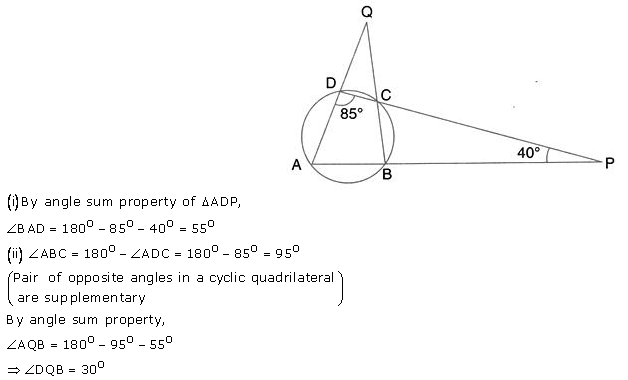
Question 48.
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = x°; find (in terms of x) the values of:
(i) ∠COB
(ii) ∠DOC
(iii) ∠DAC
(iv) ∠ADC.

Solution:

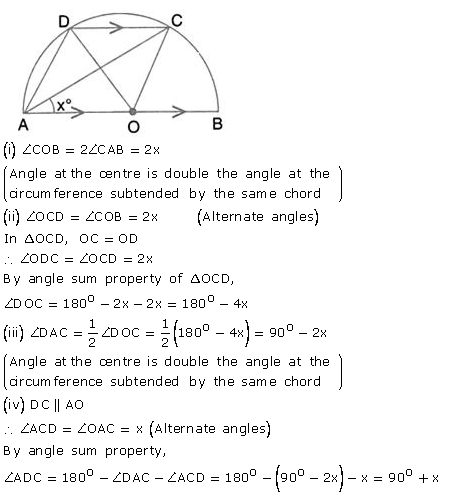
Question 49.
In the given figure, AB is the diameter of a circle with centre O. ∠BCD = 130°. Find:
(i) ∠DAB
(ii) ∠DBA

Solution:

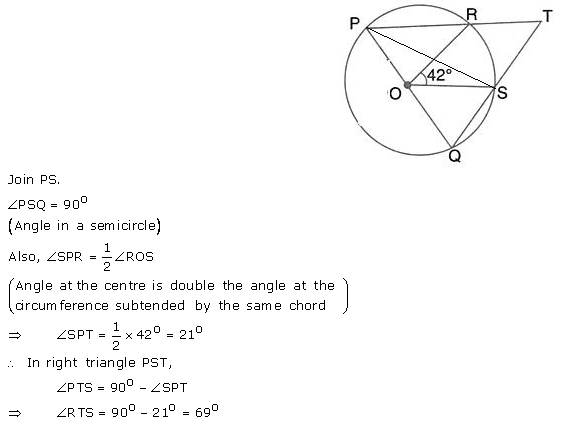
Question 50.
In the given figure, PQ is the diameter of the circle whose centre is O. Given ∠ROS = 42°; calculate ∠RTS.

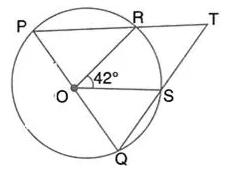
Solution:

Question 51.
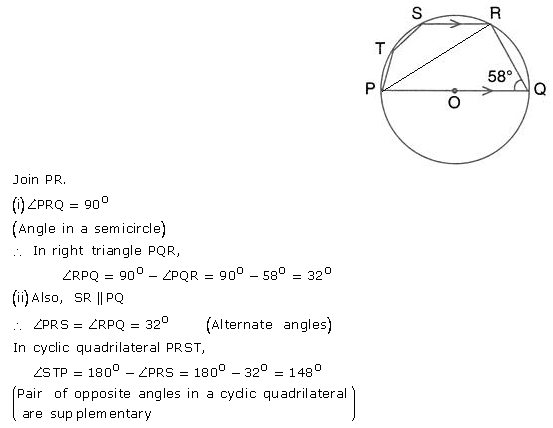
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°; calculate
(i) ∠RPQ
(ii) ∠STP.

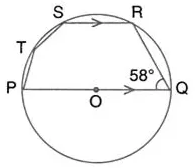
Solution:

Question 52.
AOD = 60°; calculate the numerical values of:
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠AOD = 60°; calculate the numerical values of:
(i) ∠ABD,
(ii) ∠DBC,
(iii) ∠ADC.

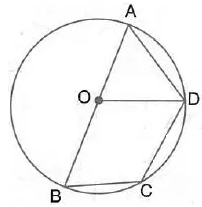
Solution:

Question 53.
In the given figure, the centre of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40″; find:
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABD,
(iv) ∠ADB.

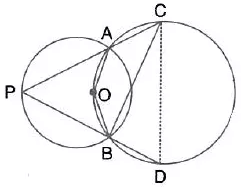
Solution:

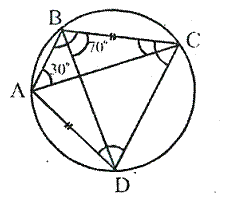
Question 54.
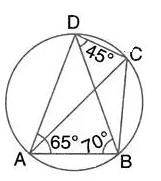
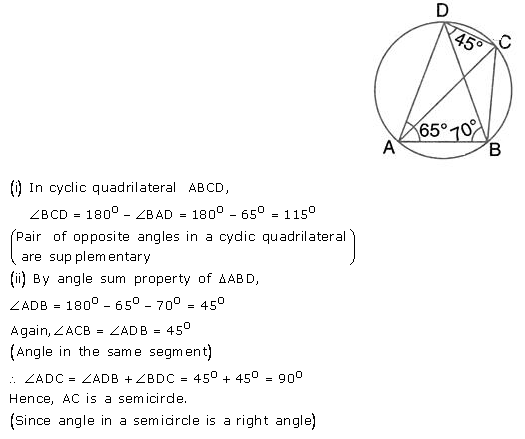
In the given figure, ∠BAD = 65°, ∠ABD = 70° and ∠BDC = 45°; find:
(i) ∠BCD,
(ii) ∠ACB.
Hence, show that AC is a diameter.

Solution:

Question 55.
In a cyclic quadrilateral ABCD, ∠A : ∠C = 3 : 1 and ∠B : ∠D = 1 : 5; find each angle of the quadrilateral.
Solution:

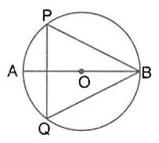
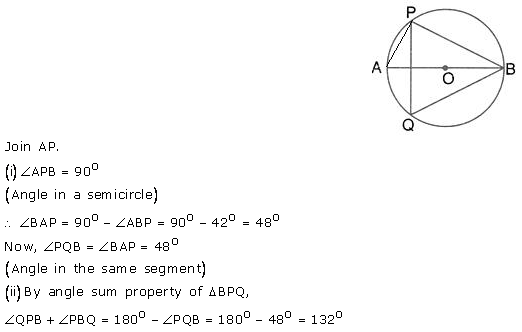
Question 56.
The given figure shows a circle with centre O and ∠ABP = 42°. Calculate the measure of
(i) ∠PQB
(ii) ∠QPB + ∠PBQ

Solution:

Question 57.
In the given figure, M is the centre of the circle. Chords AB and CD are perpendicular to each other. If ∠ MAD =x and ∠BAC = y.
(i) express ∠AMD in terms of x.
(ii) express ∠ABD in terms of y.
(iii) prove that : x = y

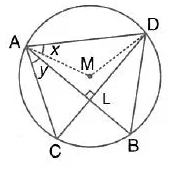
Solution:

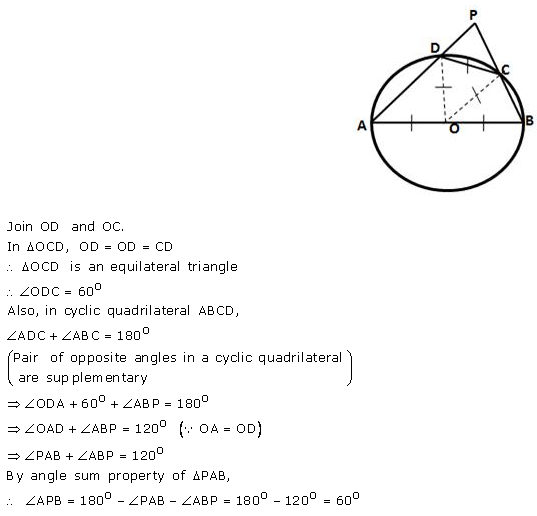
Question 61 (old).
In a circle, with centre O, a cyclic quadrilateral ABCD is drawn with AB as a diameter of the circle and CD equal to radius of the circle. If AD and BC produced meet at point P; show that ∠APB = 60°.
Solution:

Circles Exercise 17B – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal.
Prove it.
Solution:

Question 2.
In the following figure, AD is the diameter of the circle with centre 0. chords AB, BC and CD are equal. If ∠DEF = 110°, calculate:
(i) ∠ AFE,
(ii) ∠FAB.

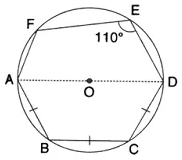
Solution:

Question 3.
If two sides of a cycli-quadrilateral are parallel; prove thet:
(i) its other two side are equal.
(ii) its diagonals are equal.
Solution:

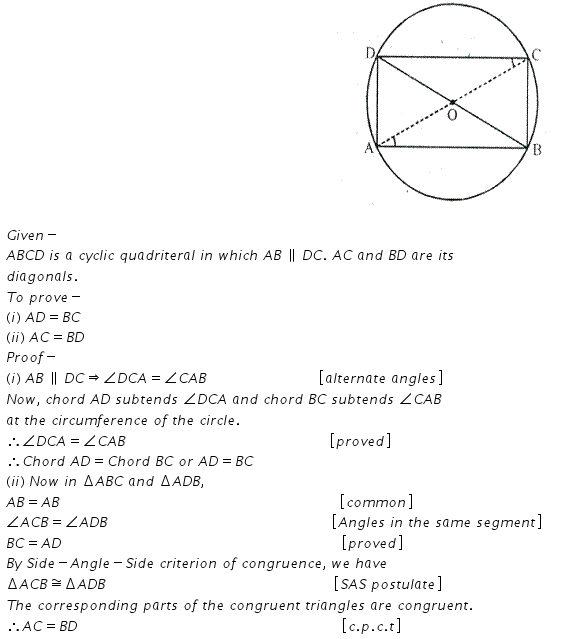
Question 4.
The given figure show a circle with centre O. also, PQ = QR = RS and ∠PTS = 75°. Calculate:
(i) ∠POS,
(ii) ∠ QOR,
(iii) ∠PQR.

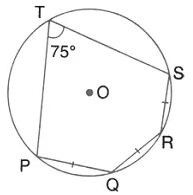
Solution:

Question 5.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. calculate the sizes of:
(i) ∠ AOB,
(ii) ∠ ACB,
(iii) ∠ABC.

Solution:

Question 6.
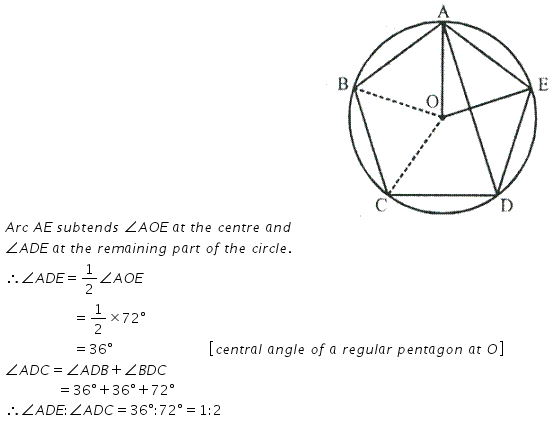
In a regular pentagon ABCDE, inscribed in a circle; find ratio between angle EDA and angel ADC.
Solution:

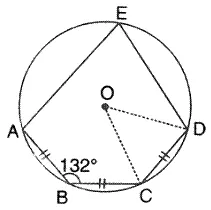
Question 7.
In the given figure. AB = BC = CD and ∠ABC = 132°, calculate:
(i) ∠AEB,
(ii) ∠ AED,
(iii) ∠COD.

Solution:

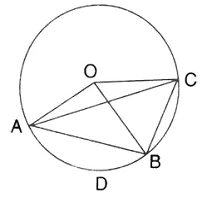
Question 8.
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find:
(i) ∠ CAB,
(ii) ∠ADB.

Solution:

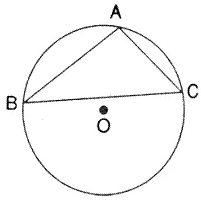
Question 9.
The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon. Find the angles of triangle ABC.

Solution:

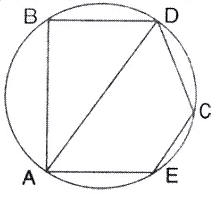
Question 10.
In the given figire, BD is a side of a regularhexagon, DC is a side of a regular pentagon and AD is adiameter. Calculate:
(i) ∠ ADC
(ii) ∠BAD,
(iii) ∠ABC
(iv) ∠ AEC.

Solution:

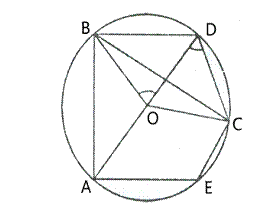
Circles Exercise 17C – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
In the given circle with diametre AB, find the value of x.

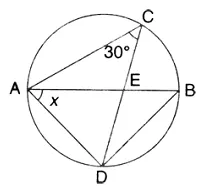
Solution:

∠ABD = ∠ACD = 30° (Angle in the same segment)
Now in ∆ ADB,
∠BAD + ∠ADB + ∠DBA = 180° (Angles of a A)
But ∠ADB = 90° (Angle in a semi-circle)
∴ x + 90° + 30° = 180° ⇒ x + 120° = 180°
∴ x= 180° – 120° = 60° Ans.

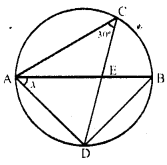
Question 1.
In the given figure, O is the centre of the circle with radius 5 cm, OP and OQ are perpendiculars to AB and CD respectively. AB = 8cm and CD = 6cm. Determine the length of PQ.

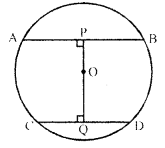
Solution:

Question 2.
In the given figure, ABC is a triangle in which ∠ BAC = 30° Show that BC is equal to the radius of the circum-circle of the triangle ABC, whose centre is O.

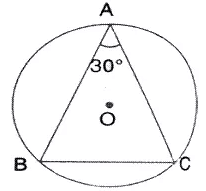
Solution:

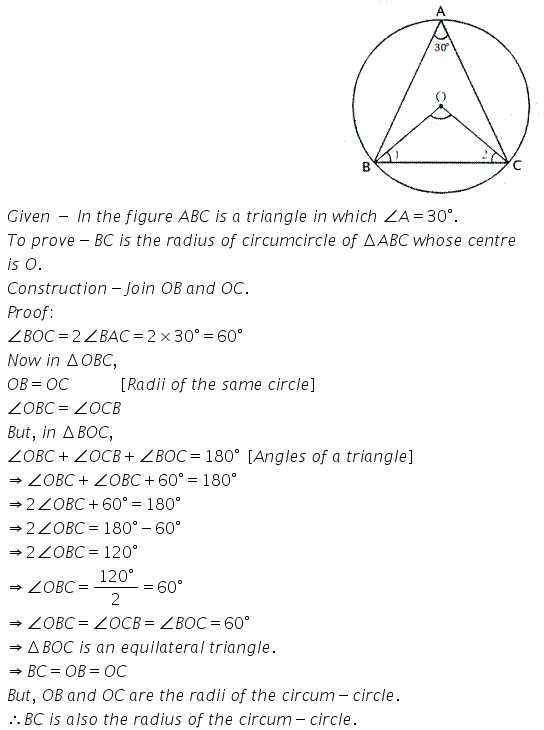
Question 3.
Prove that the circle drawn on any one a the equalside of an isoscele triangle as diameter bisects the base.
Solution:

Question 3 (old).
The given figure show two circles with centres A and B; and radii 5 cm and 3cm respectively, touching each other internally. If the perpendicular bisector of AB meets the bigger circle in P and Q, find the length of PQ.

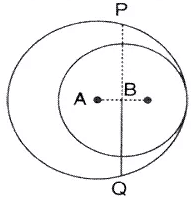
Solution:

Question 4.
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠ CBE = 65°, calculate ∠DEC.

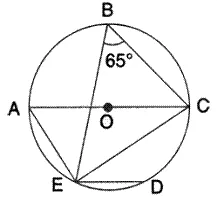
Solution:

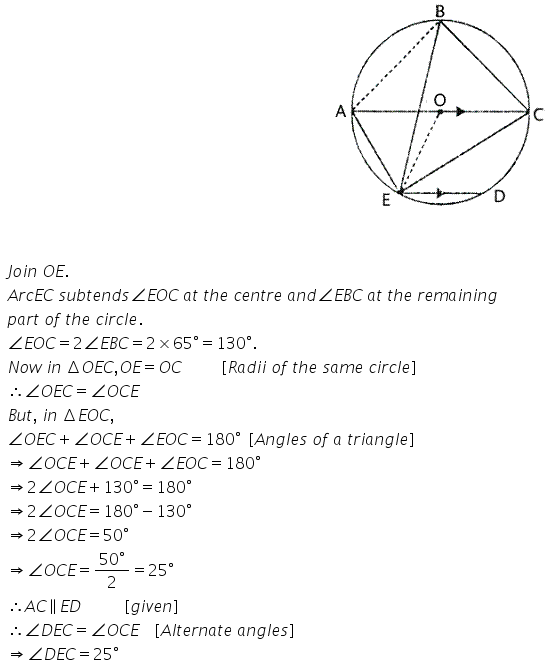
Question 5.
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. Prove it.
Solution:

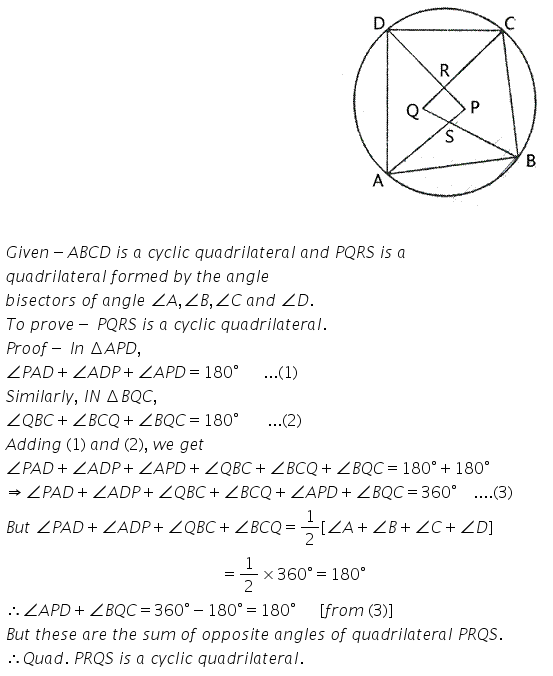
Question 6.
In the figure, ∠DBC = 58°. BD is a diameter of the circle. Calculate:
(i) ∠BDC
(ii) ∠BEC
(iii) ∠BAC

Solution:

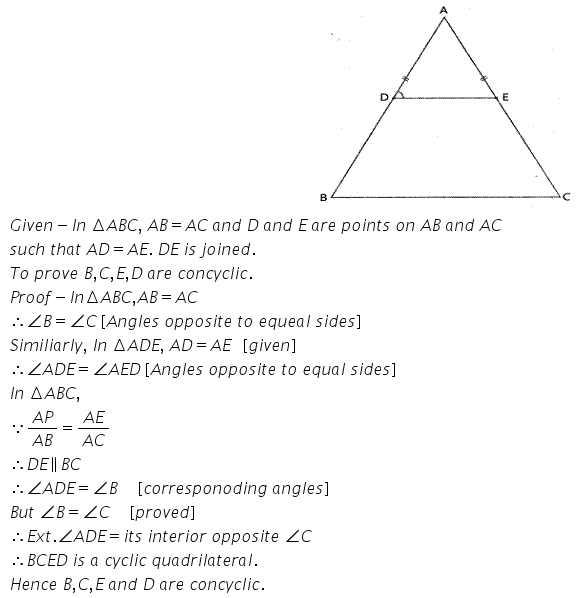
Question 7.
D and E are points on equal sides AB and AC of an isosceles triangle ABC such that AD = AE. Provet that the points B, C, E and D are concyclic.
Solution:

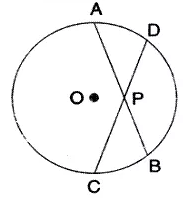
Question 7 (old).
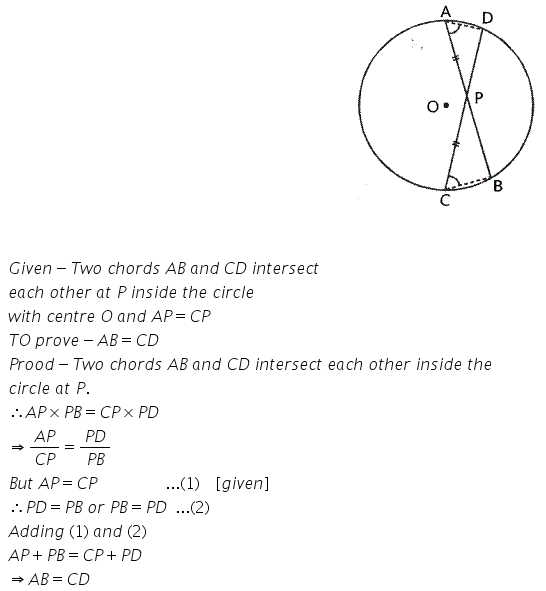
Chords AB and CD of a circle intersect each other at point P such that AP = CP.
Show that: AB = CD.

Solution:

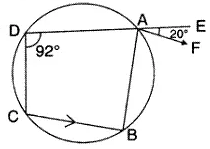
Question 8.
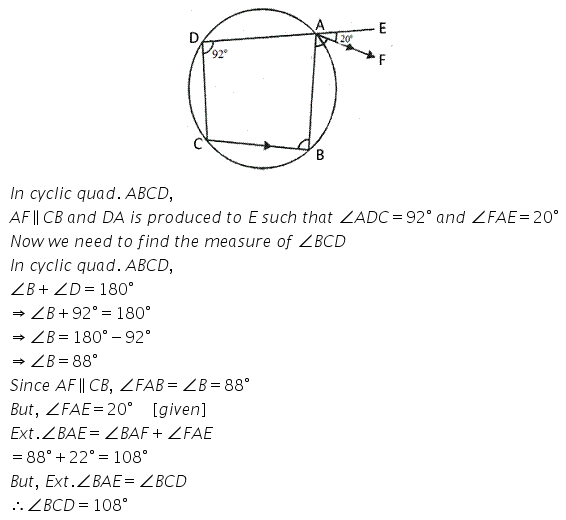
In the given rigure, ABCD is a cyclic eqadrilateral. AF is drawn parallel to CB and DA is produced to point E. If ∠ ADC = 92°, ∠ FAE = 20°; determine ∠ BCD. Given reason in support of your answer.

Solution:

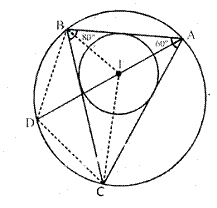
Question 9.
If I is the incentre of triangle ABC and Al when produced meets the cicrumcircle of triangle ABC in points D. if ∠ BAC = 66° and ∠ = 80o.calculate:
(i) ∠ DBC
(ii) ∠ IBC
(iii) ∠ BIC.

Solution:

Question 10.
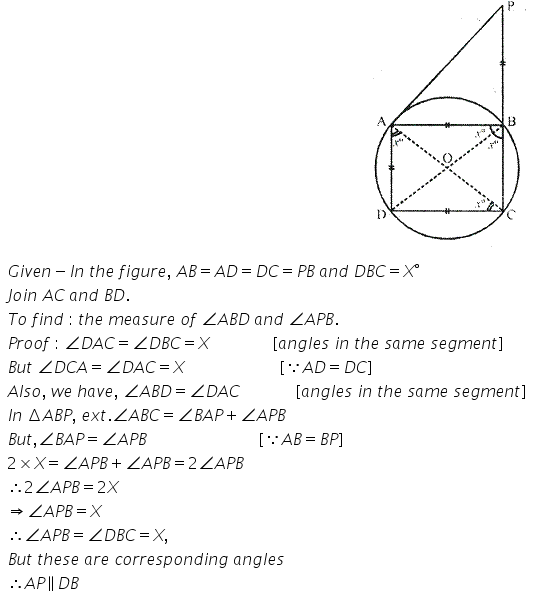
In the given figure, AB = AD = DC = PB and ∠ DBC = x°. Determine, in terms of x:
(i) ∠ ABD,
(ii) ∠ APB.
Hence or otherwise, prove thet AP is parallel to DB.

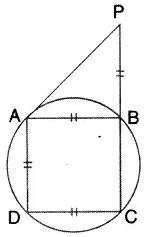
Solution:

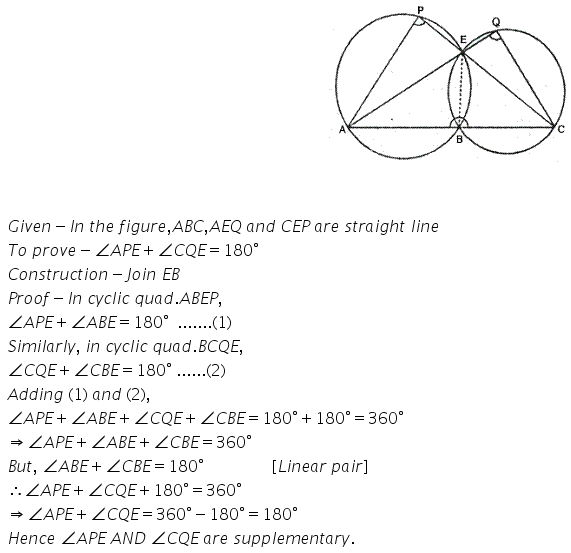
Question 11.
In the given figure; ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠ CQE are supplementary.

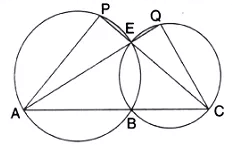
Solution:

Question 12.
In the given, AB is the diameter of the circle with centre O.

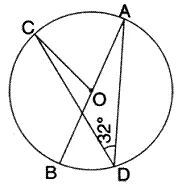
If ∠ ADC = 32°, find angle BOC.
Solution:

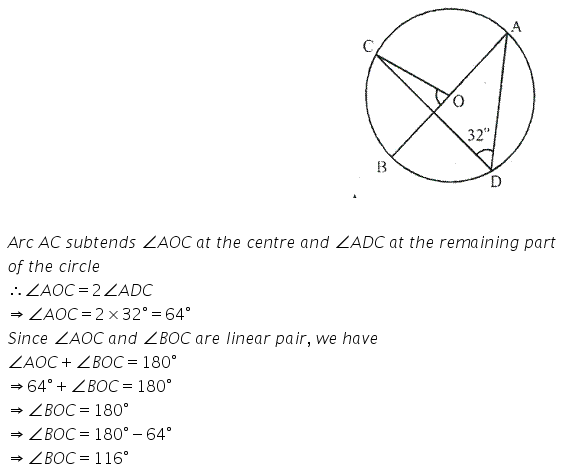
Question 13.
In a cyclic-quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ prouduced meet at point A: whereas sides PQ and SR produced meet at point B.
If ∠A: ∠B = 2 : 1;find angles A and B.
Solution:

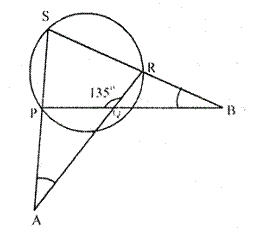
Question 17 (old).
If the following figure, AB is the diameter of a circle with centre O and CD is the chord with lengh equal radius OA.
If AC produced and BD produed meet at point p; show that ∠APB = 60°

Solution:

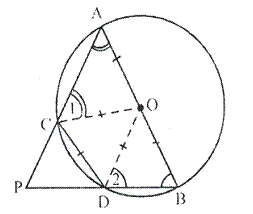
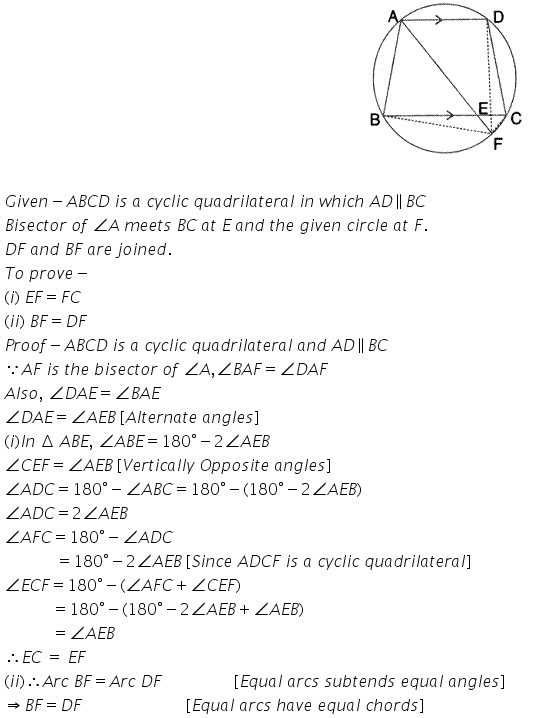
Question 14.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC.

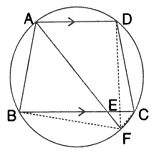
If the bisector of angle A meet BC at point E and the given circle at point F, prove that:
(i) EF = FC
(ii) BF =DF
Solution:

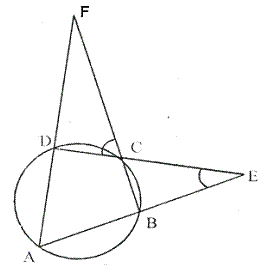
Question 15.
ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point e; whereas sides BC and AD produced meet at point F. I f ∠ DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
Solution:

Question 16.
The following figure shows a cicrcle with PR as its diameter. If PQ = 7 cm and QR = 3RS = 6 cm, Find the perimetre of the cyclic quadrilateral PORS.

Solution:

Question 17.
In the following figure, AB is the diameter of a circle with centre O. If chord AC = chord AD.prove that:
(i) arc BC = arc DB
(ii) AB is bisector of ∠ CAD.
Further if the lenghof arc AC is twice the lengthof arc BC find :
(a) ∠ BAC
(b) ∠ ABC

Solution:

Question 18.
In cyclic quadrilateral ABCD; AD = BC, ∠ = 30° and ∠ = 70°; find;
(i) ∠ BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ ADC
Solution:

Question 19.
In the given figure, ∠ACE = 43° and ∠ = 62°; find the values of a, b and c.

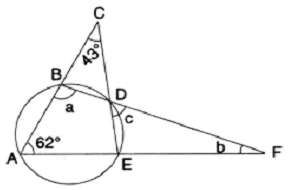
Solution:

Question 20.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠ BAC = 25°
Find
(i) ∠ CAD
(ii) ∠ CBD
(iii) ∠ ADC

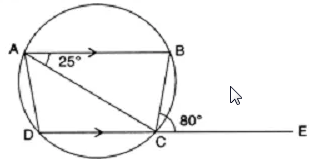
Solution:

Question 21.
ABCD is a cyclic quadrilateral of a circle with centre o such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle..if AD and BC produced meet at P, show that APB =60°
Solution:

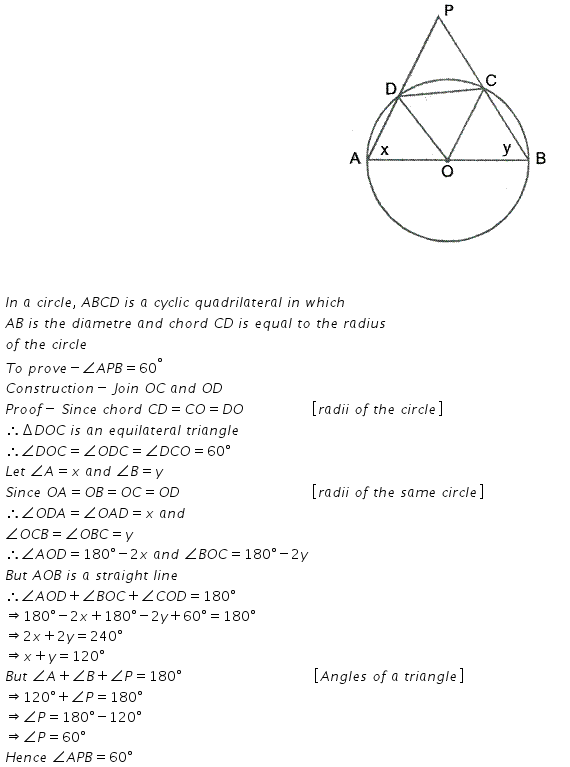
Question 22.
In the figure, given alongside, CP bisects angle ACB. Show that DP bisects angle ADB.

Solution:

Question 23.
In the figure, given below, AD = BC, ∠ BAC = 30° and ∠ = 70° find:
(i) ∠ BCD
(ii) ∠ BCA
(iii) ∠ ABC
(iv) ∠ADC

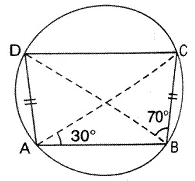
Solution:

Question 24.
In the figure given below, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED (2016)
Solution:
i. AD is parallel to BC, i.e., OD is parallel to BC and BD is transversal.

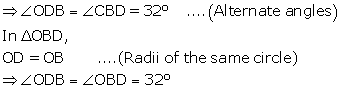
Question 25.
In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
i. ∠BCD
ii. ∠BOD
iii. ∠OBD

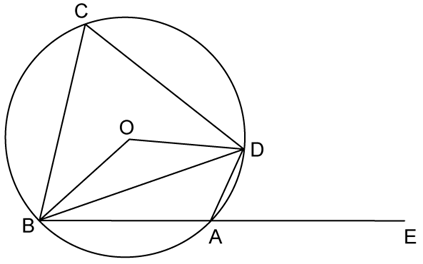
Solution:
∠DAE and ∠DAB are linear pair
So,
∠DAE + ∠DAB = 180°
∴∠DAB = 110°

Also,
∠BCD + ∠DAB = 180°……Opp. Angles of cyclic quadrilateral BADC
∴∠BCD = 70°
∠BCD = \(\frac { 1 }{ 2 }\) ∠BOD…angles subtended by an arc on the centre and on the circle
∴∠BOD = 140°

In ΔBOD,
OB = OD……radii of same circle
So,
∠OBD =∠ODB……isosceles triangle theorem
∠OBD + ∠ODB + ∠BOD = 180°……sum of angles of triangle
2∠OBD = 40°
∠OBD = 20°

More Resources for Selina Concise Class 10 ICSE Solutions

• Selina Maths Class 10 ICSE Solutions
• Selina ICSE Physics Class 10 Solutions
• Concise Chemistry Class 10 ICSE Guide Pdf
• Selina ICSE Class 10 Biology Solutions

ICSE Solutions Selina ICSE Solutions