Math Labs with Activity – Verify the Identity (a² – b²) = (a+b)(a-b) (Method 1)

by

Math Labs with Activity – Verify the Identity (a² – b²) = (a+b)(a-b) (Method 1)

OBJECTIVE

To verify the identity (a² – b²) = (a+b)(a-b) (Method 1)

Materials Required

  1. A piece of cardboard
  2. A sheet of white paper
  3. A geometry box
  4. A tube of glue
  5. A coloured glazed paper
  6. A pair of scissors

Procedure
We shall verify the identity for a = 10, b = 3.
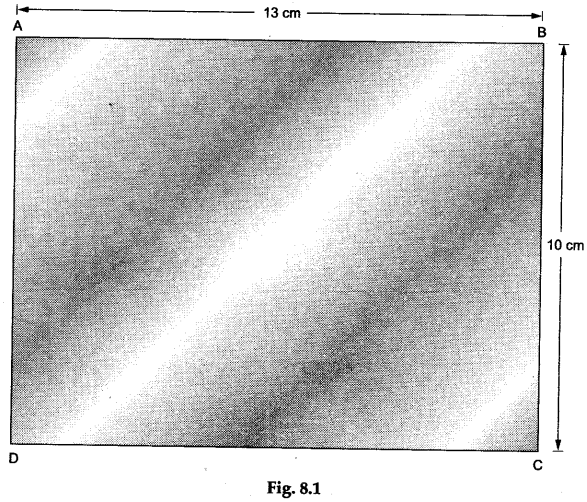
Step 1: Paste the white paper on the cardboard. Draw a rectangle ABCD of length AB = 13 cm and breadth BC = 10 cm on this paper as shown in Figure 8.1.
Math Labs with Activity - Verify the Identity (a² - b²) = (a+b)(a-b) (Method 1) 1
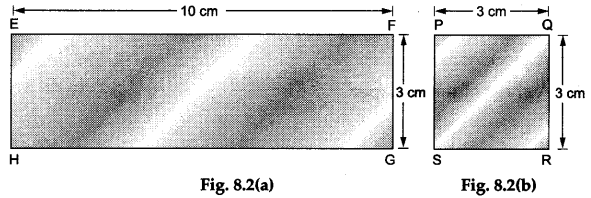
Step 2: Cut a rectangle EFGH of length EF = 10 cm and breadth FG = 3 cm from the coloured glazed paper as shown in Figure 8.2(a). Also, cut a square PQRS of side 3 cm as shown in Figure 8.2(b).
Math Labs with Activity - Verify the Identity (a² - b²) = (a+b)(a-b) (Method 1) 2
Step 3: Paste the rectangle EFGH over the rectangle ABCD such that the side EH falls on the side AD and the point H falls on the point D as shown in Figure 8.3.
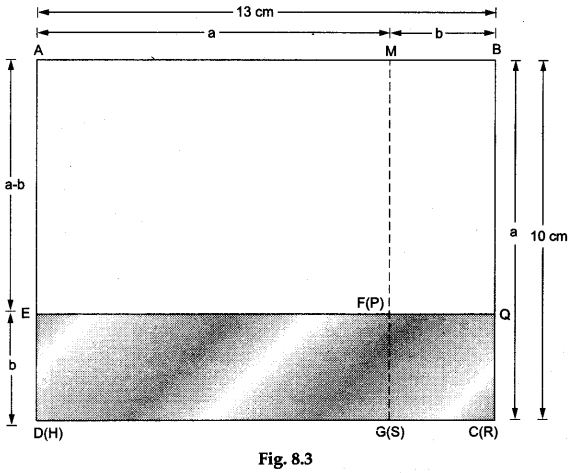
Math Labs with Activity - Verify the Identity (a² - b²) = (a+b)(a-b) (Method 1) 3
Step 4: Paste the square PQRS over the rectangle ABCD such that the side QR falls on the side BC and the point R falls on the point C as shown in Figure 8.3.
Step 5: Produce the line GF to meet the side AB at a point M as shown in Figure 8.3.

Observations and Calculations

  1. Area of rectangle ABQE = (a+b)(a- b).
  2. Area of rectangle ABCD =(a+b)a.
    Area of rectangle EFGH = ab.
    Area of square PQRS = b².
    area of rect. ABQE = (area of rect. ABCD) – (area of rect. EFGH) – (area of square PQRS) =(a+b)a-ab-b² = a² + ab-ab -b² = a²-b².
  3. Equating the two values of the area of rectangle ABQE, we get
    (a² – b²) = (a+b)(a-b).

Result
The identity (a² – b²) = (a+b)(a-b) is verified.

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills

Leave a Comment