How do you Transpose a Matrix?
Transpose of a matrix
The matrix obtained from a given matrix A by changing its rows into columns or columns into rows is called transpose of matrix A and is denoted by AT or A′.
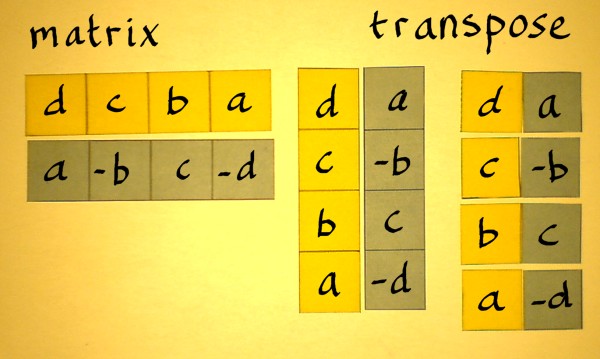From the definition it is obvious that if order of A is m × n, then order of AT is n × m.
Example:
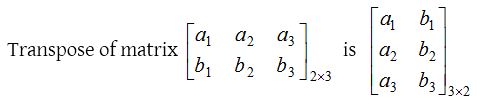
Properties of transpose
Let A and B be two matrices then,
- (AT)T = A
- (A + B)T = AT + BT, A and B being of the same order
- (kA)T = kAT, k be any scalar (real or complex)
- (AB)T = BTAT, A and B being conformable for the product AB
- (A1 A2 A3 …… An-1 An)T = AnT An-1T ……. A3T A2T A1T
- IT = I
Symmetric and Skew-symmetric Matrices
(1) Symmetric matrix :
A square matrix A = [aij] is called symmetric matrix if aij = aji for all i, j or AT = A.
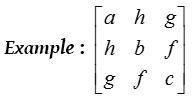
(2) Skew-symmetric matrix :
A square matrix A = [aij] is called skew- symmetric matrix if aij = −aji for all i, j or AT = −A.
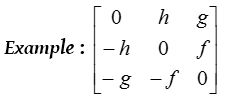
All principal diagonal elements of a skew- symmetric matrix are always zero because for any diagonal element.
aij = −aji ⇒ aij = 0
Properties of symmetric and skew-symmetric matrices
- If A is a square matrix, then A + AT, AAT, ATA are symmetric matrices, while A − AT is skew- symmetric matrix.
- If A is a symmetric matrix, then −A, KA, AT, An, A−1, BT AB are also symmetric matrices, where n ∈ N, K ∈ R and B is a square matrix of order that of A.
- If A is a skew-symmetric matrix, then
(a) A2n is a symmetric matrix for n ∈ N.
(b) A2n+1 is a skew-symmetric matrix for n ∈ N.
(c) kA is also skew-symmetric matrix, where k ∈ R.
(d) BT AB is also skew- symmetric matrix where B is a square matrix of order that of A. - If A, B are two symmetric matrices, then
(a) A ± B, AB + BA are also symmetric matrices,
(b) AB – BA is a skew- symmetric matrix,
(c) AB is a symmetric matrix, when AB = BA. - If A, B are two skew-symmetric matrices, then
(a) A ± B, AB – BA are skew-symmetric matrices,
(b) AB + BA is a symmetric matrix. - If A a skew-symmetric matrix and C is a column matrix, then CT AC is a zero matrix.