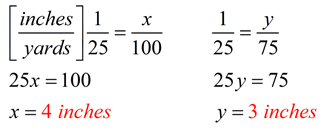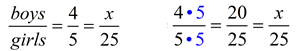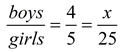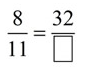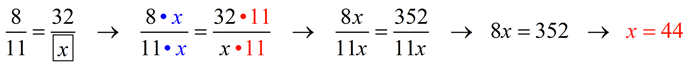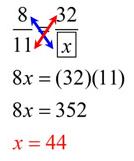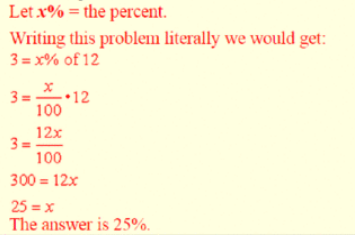Order of Operations and Evaluating Expressions
Order of Operations
When a numerical expression involves two or more operations, there is a specific order in which these operations must be performed.
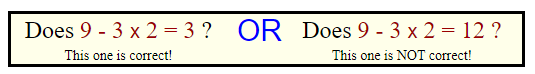
When evaluating an expression, proceed in this order:
- parentheses are done first.
- exponents are done next.
- multiplication and division are done as they are encountered from left to right.
- addition and subtraction are done as they are encountered from left to right.
The proper application of “order of operations” is needed when working with such mathematical topics as evaluating formulas, solving equations, evaluating algebraic expressions, and simplifying monomials and polynomials.
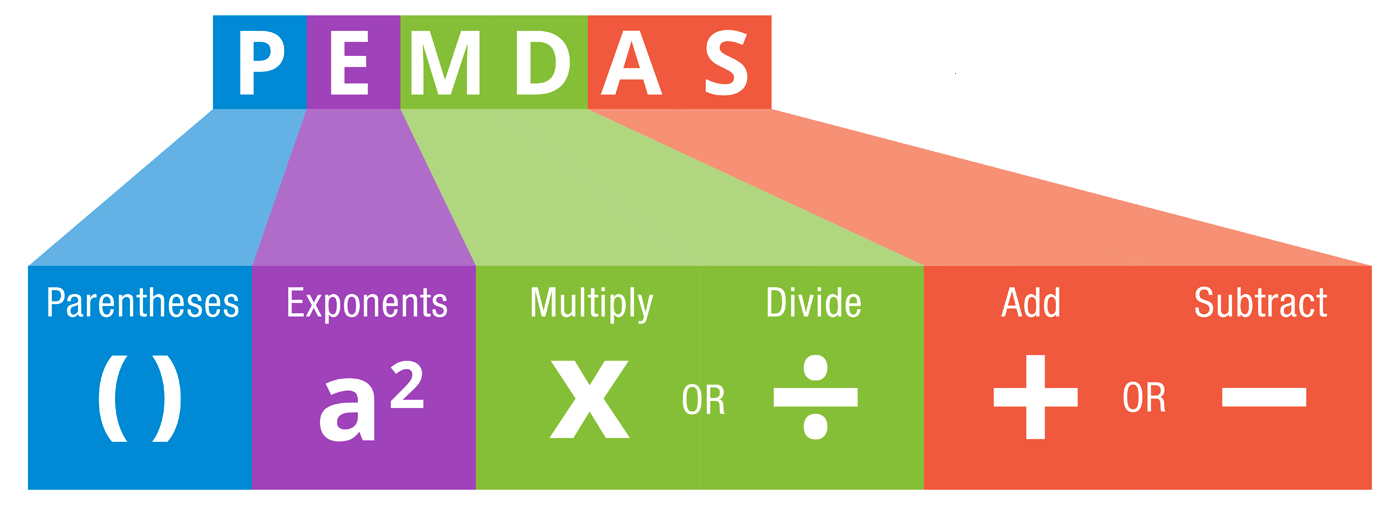
There is a phrase that may help you to remember this order: PEMDAS
Parenthesis, Exponents, (Multiplication/Division), (Add/Subtract)
While PEMDAS lists M before D, remember that multiplication and division are done as they are read from left to right. It may not always be the case that multiplication is done “before” division.
The expression 16 ÷ 4 x 2 = 8 (not 2).
The same is true of addition and subtraction: 8 – 4 + 2 = 6 (not 2).
The reason (multiplication & division – MD) and (add & subtract – AS) are “grouped” in sets of parentheses is that when those operations are next to each other you do the math from left to right. You do not always do multiplication or addition first. It may be the case where division will be done BEFORE multiplication or subtraction will be done BEFORE addition.
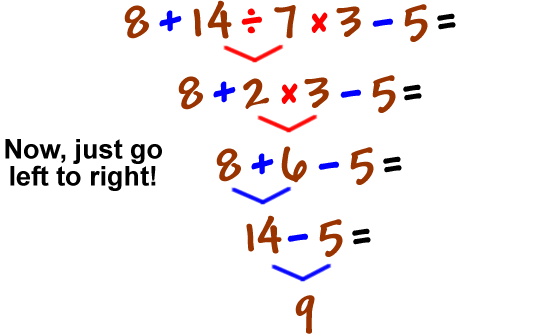
Read More:
- Integers and Examples
- Fundamental Operations on Integers
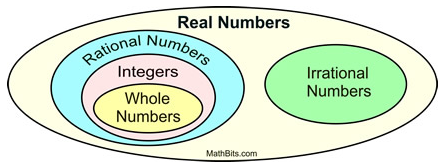
- Whole Numbers And Its Properties
- Hints for Remembering the Properties of Real Numbers
- What Are The Four Basic Operations In Mathematics
- Absolute Value
It may be helpful to build a PEMDAS table. Check off the operation after it has been performed. For operations that are not part of the problem, place a hyphen.
- Simplify any parenthesis first, starting with the inner most group, and check off the “P” box.
- Simplify any powers ( exponents) and check off the “E” box.
- Perform the multiplication and division in order from left to right and check off the “M” & “D” boxes.
- Do the addition and subtraction last. Remember, if the operations are written next to each other work from left to right and check off the last two boxes.
When there are two or more parenthesis, or grouping symbols, perform the inner most grouping symbol first.
Example 1: Simplify 40 – 2(6 – 4)2

Example 2: Simplify 30 – (8 – 15 ÷ 3) × 2

Example 3: Simplify: 2(20 – 32 + 1) – (42 ÷ 2 × 3)

It is very important to understand that it DOES make a difference if the order is not performed correctly!!!
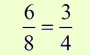
 In each proportion the first and last terms (4 and 2) are called the extremes. The second and third terms (8 and 1) are called the means.
In each proportion the first and last terms (4 and 2) are called the extremes. The second and third terms (8 and 1) are called the means.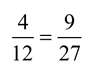
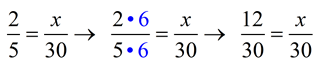
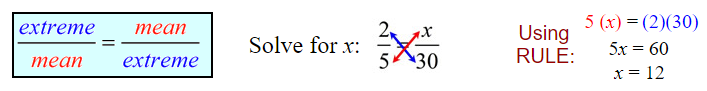

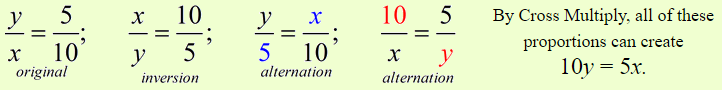
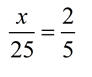 Solution:
Solution: