Rational Numbers

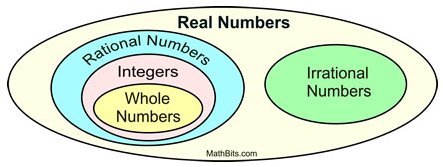
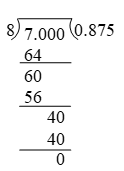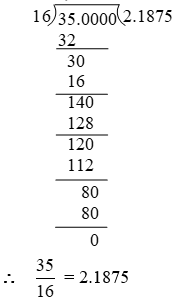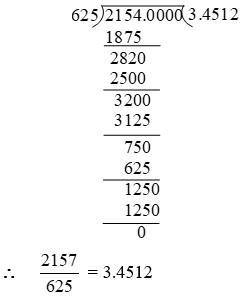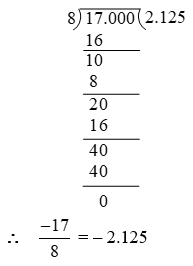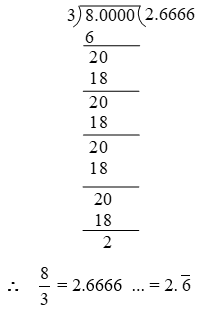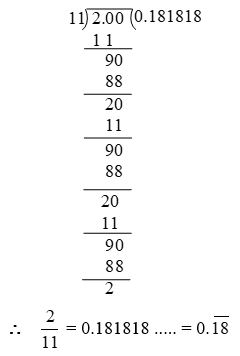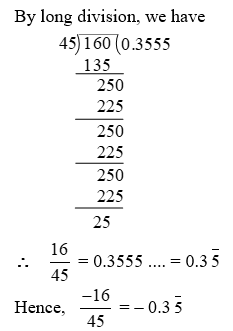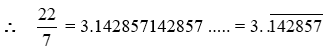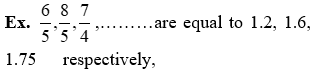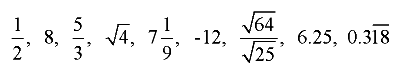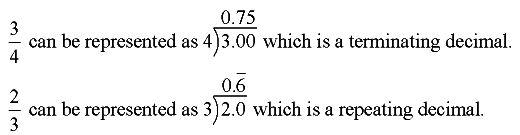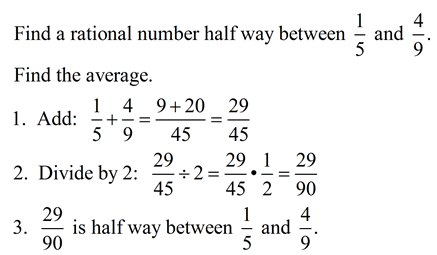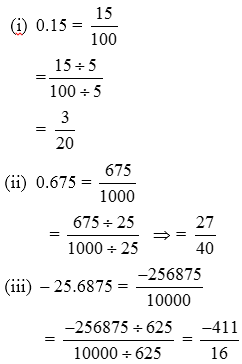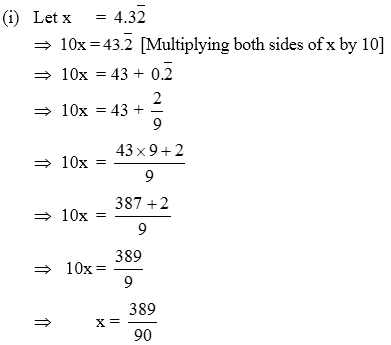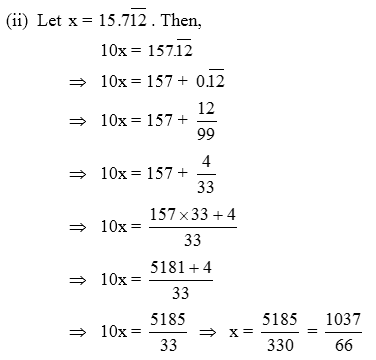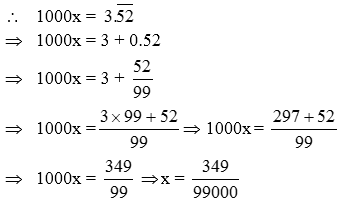Conversion Of Decimal Numbers Into Rational Numbers Of The Form m/n

Case I: When the decimal number is of terminating nature.
Algorithm:

• Step-1: Obtain the rational number.
• Step-2: Determine the number of digits in its decimal part.
• Step-3: Remove decimal point from the numerator. Write 1 in the denominator and put as many zeros on the right side of 1 as the number of digits in the decimal part of the given rational number.
• Step-4: Find a common divisor of the numerator and denominator and express the rational number to lowest terms by dividing its numerator and denominator by the common divisor.

Case II: When decimal representation is of non-terminating repeating nature.
In a non terminating repeating decimal, there are two types of decimal representations

1. A decimal in which all the digit after the decimal point are repeated. These type of decimals are known as pure recurring decimals.
   For Example: \(0.\overline{6},\,\,0.\overline{16},\,\,0.\overline{123}\) are pure recurring decimals.
2. A decimal in which at least one of the digits after the decimal point is not repeated and then some digit or digits are repeated. This type of decimals are known as mixed recurring decimals.
   For Example: \(2.1\overline{6},\,\,0.3\overline{5},\,\,0.7\overline{85}\) are mixed recurring decimals.

Conversion Of A Pure Recurring Decimal To The Form p/q

Algorithm:

• Step-1: Obtain the repeating decimal and pur it equal to x (say)
• Step-2: Write the number in decimal form by removing bar from the top of repeating digits and listing repeating digits at least twice. For sample, write x = \(0.\overline{8}\) as x = 0.888…. and x = \(0.\overline{14}\) as x = 0.141414……
• Step-3: Determine the number of digits having bar on their heads.
• Step-4: If the repeating decimal has 1 place repetition, multiply by 10; a two place repetition, multiply by 100; a three place repetition, multiply by 1000 and so on.
• Step-5: Subtract the number in step 2 from the number obtained in step 4
• Step-6: Divide both sides of the equation by the coefficient of x.
• Step-7: Write the rational number in its simplest form.

Conversion Of A Mixed Recurring Decimal To The Form p/q

Algorithm:

• Step-1 : Obtain the mixed recurring decimal and write it equal to x (say)
• Step-2 : Determine the number of digits after the decimal point which do not have bar on them. Let there be n digits without bar just after the decimal point
• Step-3 : Multiply both sides of x by 10ⁿ  so that only the repeating decimal is on the right side of the decimal point.
• Step-4 : Use the method of converting pure recurring decimal to the form p/q and obtain the value of x

Conversion Of Decimal Numbers Into Rational Numbers Example Problems With Solutions

Example 1:    Express each of the following numbers in the form p/q.
(i) 0.15                        (ii) 0.675                       (iii) –25.6875
Solution:    

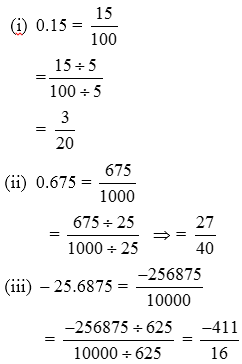
Example 2:    Express each of the following decimals in the form p/q.
\(\text{(i) 0}\text{.}\overline{\text{6}}\text{ (ii) 0}\text{.}\overline{\text{35}}\text{ (iii) 0}\text{.}\overline{\text{585}}\)
Solution:    


The above example suggests us the following rule to convert a pure recurring decimal into a rational number in the form p/q.

Example 3:    Convert the following decimal numbers in the form p/q.
\(\text{(i) }5.\bar{2}\text{ (ii) }23.\overline{43}\)
Solution:    

Example 4:    Express the following decimals in the form
\(\text{(i) }0.3\overline{2}\text{           (ii) }0.12\overline{3}\)
Solution:    

Example 5:    Express each of the following mixed recurring decimals in the form p/q
\(\text{(i) }4.3\overline{2}\text{           (ii) }15.7\overline{12}\)
Solution:    

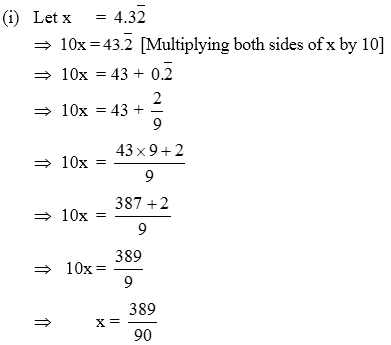
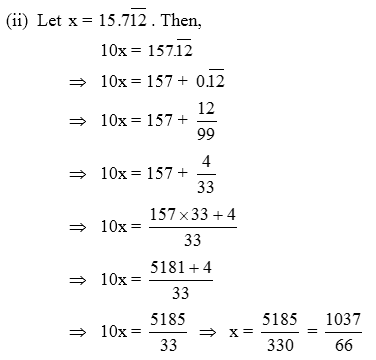
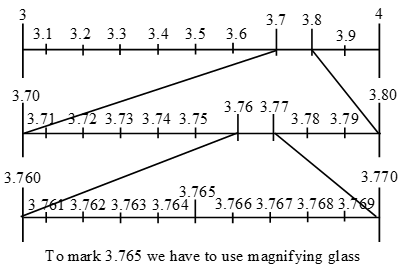
Example 6:    Represent 3.765 on the number line.
Solution:    This number lies between 3 and 4. The distance 3 and 4 is divided into 10 equal parts. Then the first mark to the right of 3 will represent 3.1 and second 3.2 and so on. Now, 3.765 lies between 3.7 and 3.8. We divide the distance between 3.7 and 3.8 into 10 equal parts 3.76 will be on the right of 3.7 at the six^th mark, and 3.77 will be on the right of 3.7 at the 7^th mark and 3.765 will lie between 3.76 and 3.77 and soon.

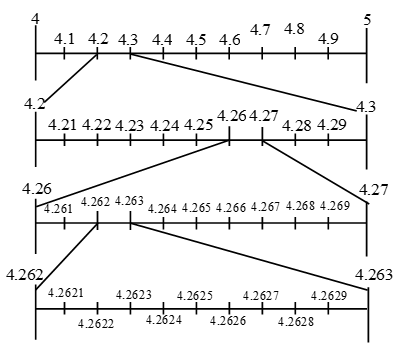
Example 7:    Visualize \(4.\overline{26}\) on the number line, upto 4 decimal places.
Solution:    We have,   \(4.\overline{26}\) = 4.2626
This number lies between 4 and 5. The distance between 4 and 5 is divided into 10 equal parts. Then the first mark to the right of 4 will represent 4.1 and second 4.2 and soon. Now, 4.2626 lies between 4.2 and 4.3. We divide the distance between 4.2 and 4.3 into 10 equal parts 4.2626 lies between 4.26 and 4.27. Again we divide the distance between 4.26 and 4.27 into 10 equal parts. The number 4.2626 lies between 4.262 and 4.263. The distance between 4.262 and 4.263 is again divided into 10 equal parts. Sixth mark from right to the 4.262 is 4.2626.

Example 8:    Express the decimal \(0.003\overline{52}\) in the form p/q
Solution:    Let x = \(0.003\overline{52}\)
Clearly, there is three digit on the right side of the decimal point which is without bar. So, we multiply both sides of x by 10³ = 1000 so that only the repeating decimal is left on the right side of the decimal point.

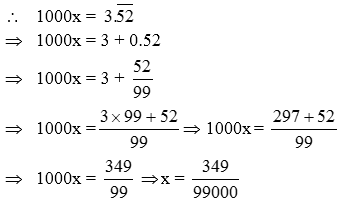
Example 9:    Give an example of two irrational numbers, the product of which is
(i) a rational number
(ii) an irrational number
Solution:    (i) The product of √27 and √3 is √81= 9, which is a rational number.
(ii) The product of √2 and √3 is √6, which is an irrational number.

Example 10:     Insert a rational and an irrational number between 2 and 3.
Solution:    If a and b are two positive rational numbers such that ab is not a perfect square of a rational number, then \(\sqrt{ab}\) is an irrational number lying between a and b. Also, if a,b are rational numbers, then \(\frac { a+b }{ 2 }\) is a rational number between them.
∴ A rational number between 2 and 3 is
\(\frac { 2+3 }{ 2 }\) = 2.5
An irrational number between 2 and 3 is
\(\sqrt{2\times 3}=\sqrt{6}\)

Example 11:     Find two irrational numbers between 2 and 2.5.
Solution:    If a and b are two distinct positive rational numbers such that ab is not a perfect square of a rational number, then \(\sqrt{ab}\) is an irrational number lying between a and b.
∴ Irrational number between 2 and 2.5 is
\( \sqrt{2\times 2.5}=\sqrt{5} \)
Similarly, irrational number between 2 and \(\sqrt{5}\) is \( \sqrt{2\times \sqrt{5}} \)
So, required numbers are \(\sqrt{5}\) and \( \sqrt{2\times \sqrt{5}} \).

Example 12:    Find two irrational numbers lying between √2 and √3.
Solution:    We know that, if a and b are two distinct positive irrational numbers, then is an irrational number lying between a and b.
∴ Irrational number between √2 and √3 is \( \sqrt{\sqrt{2}\times \sqrt{3}}=\sqrt{\sqrt{6}} \) = 6^1/4
Irrational number between √2 and 6^1/4 is \( \sqrt{\sqrt{2}\times {{6}^{1/4}}} \) = 2^1/4 × 6^1/8.
Hence required irrational number are 6^1/4 and 2^1/4 × 6^1/8

Example 13:    Find two irrational numbers between 0.12 and 0.13.
Solution:    Let a = 0.12 and b = 0.13. Clearly, a and b are rational numbers such that a < b.
We observe that the number a and b have a 1 in the first place of decimal. But in the second place of decimal a has a 2 and b has 3. So, we consider the numbers
c = 0.1201001000100001 ……
and, d = 0.12101001000100001…….
Clearly, c and d are irrational numbers such that a < c < d < b.

Example 14:    Find two rational numbers between 0.232332333233332…. and 0.252552555255552……
Solution:    Let a = 0.232332333233332….  and b = 0.252552555255552…..
The numbers c = 0.25 and d = 0.2525
Clearly, c and d both are rational numbers such that a < c < d < b.

Example 15:    Find a rational number and also an irrational number between the numbers a and b given below:
a = 0.101001000100001….,  b = 0.1001000100001…
Solution:   Since the decimal representations of a and b are non-terminating and non-repeating. So,
a and b are irrational numbers.
We observed that in the first two places of decimal a and b have the same digits. But in the third place of decimal a has a 1 whereas b has zero.
∴ a > b
Construction of a rational number between a and b : As mentioned above, first two digits after the decimal point of a and b are the same. But in the third place a has a 1 and b has a zero. So, if we consider the number c given by
c = 0.101
Then, c is a rational number as it has a terminating decimal representation.
Since b has a zero in the third place of decimal and c has a 1.
∴ b < c
We also observe that c < a, because c has zeros in all the places after the third place of decimal whereas the decimal representation of a has a 1 in the sixth place.
Thus, c is a rational number such that
b < c < a.
Hence , c is the required rational number between a and b.
Construction of an irrational number between a and b : Consider the number d given by
d = 0.1002000100001……
Clearly, d is an irrational number as its decimal representation is non-terminating and non-repeating.
We observe that in the first three places of their decimal representation b and d have the same digits but in the fourth place d and a 2 whereas b has only a 1.
∴ d > b
Also, comparing a and d, we obtain a > d
Thus, d is an irrational number such that
b < d < a.

Example 16:    Find one irrational number between the number a and b given below :
a = 0.1111….. = \(0.\bar{1}\) and b = 0.1101
Solution:    Clearly, a and b are rational numbers, since a has a repeating decimal and b has a terminating decimal. We observe that in the third place of decimal a has a 1, while b has a zero.
∴ a > b
Consider the number c given by
c = 0.111101001000100001…..
Clearly, c is an irrational number as it has non-repeating and non-terminating decimal representation.
We observe that in the first two places of their decimal representations b and c have the same digits. But in the third place b has a zero whereas c has a 1.
∴ b < c
Also, c and a have the same digits in the first four places of their decimal representations but in the fifth place c has a zero and a has a 1.
∴ c < a
Hence, b < c < a
Thus, c is the required irrational number between a and b.

Maths