Selina Concise Mathematics Class 6 ICSE Solutions Chapter 21 Framing Algebraic Expressions (Including Evaluation)
Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 21 Framing Algebraic Expressions (Including Evaluation)
ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download option. Selina Publishers Concise Mathematics for Class 6 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.
Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics
Framing Algebraic Expressions Exercise 21 – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Write in the form of an algebraic expression :
(i) Perimeter (P) of a rectangle is two times the sum of its length (l) and its breadth (b).
(ii) Perimeter (P) of a square is four times its side.
(iii) Area of a square is square of its side.
(iv) Surface area of a cube is six times the square of its edge.
Solution:
(i) Let P be the perimeter and / be the length, and b be the breadth.
P = 2 (l + b)
(ii) Let P be the perimeter and a be the side of the square.
P = 4a
(iii) Let A be the area of the square and a be the sides of the square.
A = (a)2
(iv) Let S be the surface area and a be the edges of the cube.
S = 6a2
Question 2.
Express each of the following as an algebraic expression :
(i) The sum of x and y minus m.
(ii) The product of x and y divided by m.
(iii) The subtraction of 5m from 3n and then adding 9p to it.
(iv) The product of 12, x, y and z minus the product of 5, m and n.
(v) Sum of p and 2r – s minus sum of a and 3n + 4x.
Solution:
(i) x + y – m
(ii) \(\frac { xy }{ m }\)
(iii) 3n – 5m + 9p
(iv) 12xyz – 5mn
(v) p + 2r – s – (a + 3n + 4x)
Question 3.
Construct a formula for the following :
Total wages (₹ W) of a man whose basic wage is (₹ B) for t hours week plus (₹ R) per hour, if he Works a total of T hours.
Solution:
Wages for t hours = ₹ B
Wages for overtime = R(T – t)
=> Total wages = Wages for t hours + wages for overtime of (T – t) hours
=> ₹ W = ₹ B + ₹ R (T – t)
Question 4.
If x = 4, evaluate :
(i) 3x + 8
(ii) x2 – 2x
(iii) \(\frac { { x }^{ 2 } }{ 2 }\)
Solution:
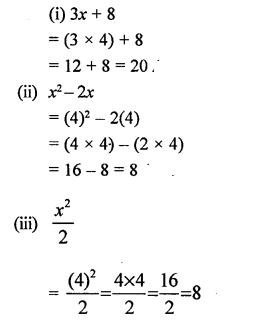
Question 5.
If m – 6, evaluate :
(i) 5m – 6
(ii) 2m2 + 3m
(iii) (2m)2
Solution:
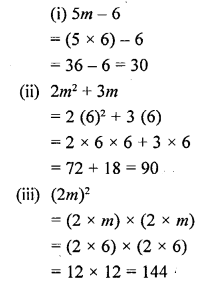
Question 6.
If x = 4, evaluate :
(i) 12x + 7
(ii) 5x2 + 4x
(iii) \(\frac { { x }^{ 2 } }{ 8 }\)
Solution:
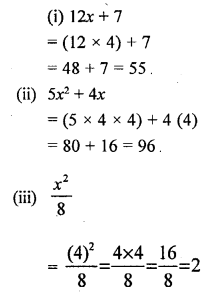
Question 7.
If m = 2, evaluate :
(i) 16m – 7
(ii) 15m2 – 10m
(iii) \(\frac { 1 }{ 4 } \times { m }^{ 3 }\)
Solution:
16m – 7
= (16 x 2) – 7
= 32 – 7 = 25
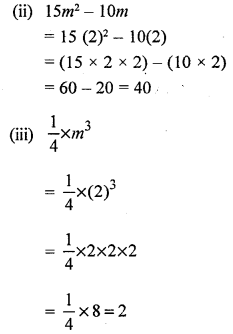
Question 8.
If x = 10, evaluate :
(i) 100x + 225
(ii) 6x2 – 25x
(iii) \(\frac { 1 }{ 50 } \times { x }^{ 3 }\)
Solution:
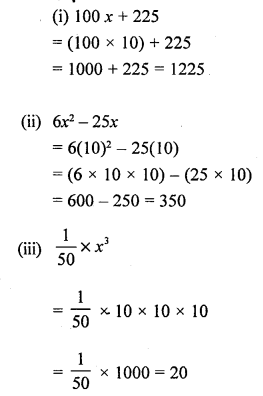
Question 9.
If a = – 10, evaluate :
(i) 5a
(ii) a2
(iii) a3
Solution:
(i)5a
= 5 x (-10) = -50
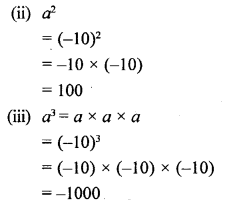
Question 10.
If x = – 6, evaluate :
(i) 11x
(ii) 4x2
(iii) 2x3
Solution:
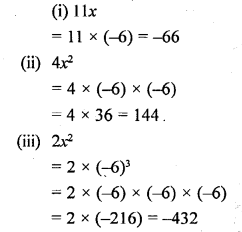
Question 11.
If m = – 7, evaluate :
(i) 12m
(ii) 2m2
(iii) 2m3
Solution:
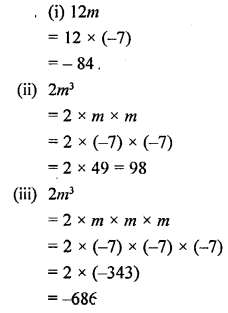
Question 12.
Find the average (A) of four quantities p, q, r and s. If A = 6, p = 3, q = 5 and r = 7 ; find the value of s.
Solution:
Given, average of four quantities (A) = 6
and p = 3,q = 5, r = 7 and s = ?
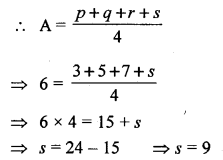
Question 13.
If a = 5 and b = 6, evaluate :
(i) 3ab
(ii) 6a2b
(iii) 2b2
Solution:
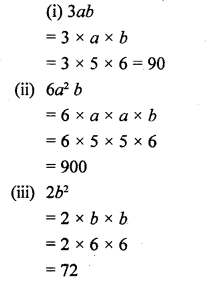
Question 14.
If x = 8 and y = 2, evaluate :
(i) 9xy
(ii) 5x2y
(iii) (4y)2
Solution:
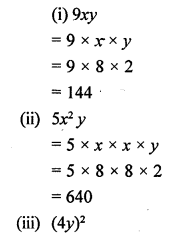
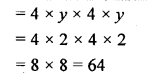
Question 15.
If x = 5 and y = 4, evaluate :
(i) 8xy
(ii) 3x2y
(iii) 3y2
Solution:
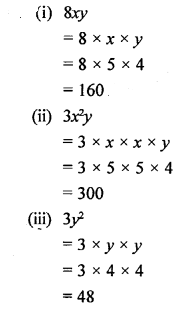
Question 16.
If y = 5 and z = 2, evaluate :
(i) 100yz
(ii) 9y2z
(iii) 5y2
(iv) (5z)3
Solution:
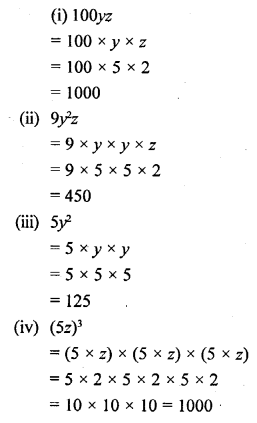
Question 17.
If x = 2 and y = 10, evaluate :
(i) 30xy
(ii) 50xy2
(iii) (10x)2
(iv) 5y2
Solution:
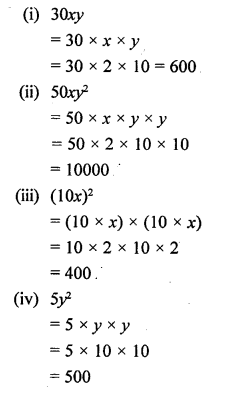
Question 18.
If m = 3 and n = 7, evaluate :
(i) 12mn
(ii) 5mn2
(iii) (10m)2
(iv) 4n2
Solution:
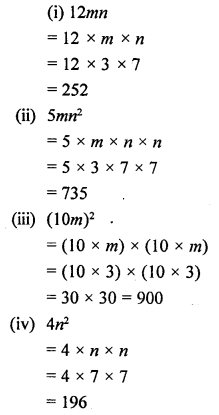
Question 19.
If a = -10, evaluate :
(i) 3a – 2
(ii) a2 + 8a
(iii) \(\frac { 1 }{ 5 }\) x a2
Solution:
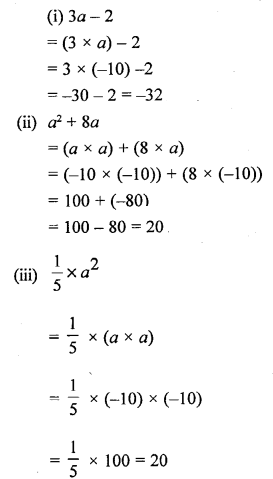
Question 20.
If x = -6, evaluate :
(i) 4x – 9
(ii) 3x2 + 8x
(iii) \(\frac { { x }^{ 2 } }{ 2 }\)
Solution:
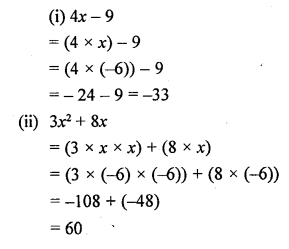
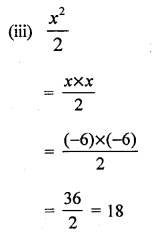
Question 21.
If m = -8, evaluate :
(i) 2m + 21
(ii) m2 + 9m
(iii) \(\frac { { m }^{ 2 } }{ 4 }\)
Solution:
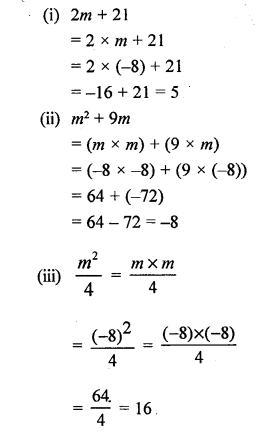
Question 22.
If p = -10, evaluate :
(i) 6p + 50
(ii) 3p2 – 20p
(iii) \(\frac { { p }^{ 2 } }{ 50 }\)
Solution:
(i) 6p + 50
= (6 x p) + 50
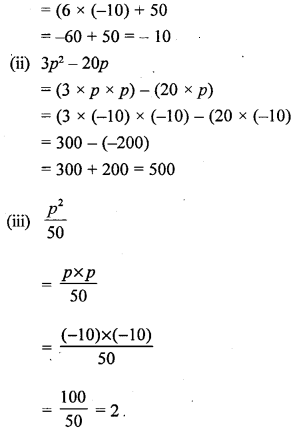
Question 23.
If y = -8, evaluate :
(i) 6y + 53
(ii) y2 + 12y
(iii) \(\frac { { y }^{ 3 } }{ 4 }\)
Solution:
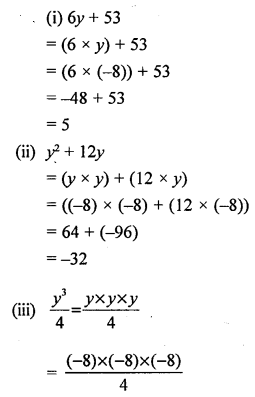
![]()
Question 24.
If x = 2 and 7 = -4, evaluate :
(i) 11xy
(ii) 5x2y
(iii) (5y)2
(iv) 8x2
Solution:
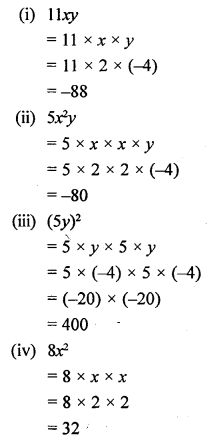
Question 25.
If m = 9 and n = -2, evaluate
(i) 4mn
(ii) 2m2n
(iii) (2n)3
Solution:
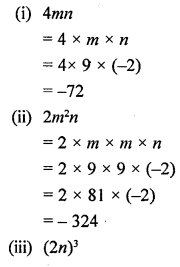
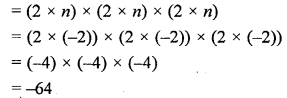
Question 26.
If m = -8 and n = -2, evaluate :
(i) 12mn
(ii) 3m2n
(iii) (4n)2
Solution:
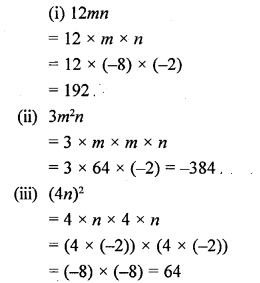
Question 27.
If x = -5 and y = -8, evaluate :
(i) 4xy
(ii) 2xy2
(iii) 4x2
(iv) 3y2
Solution:
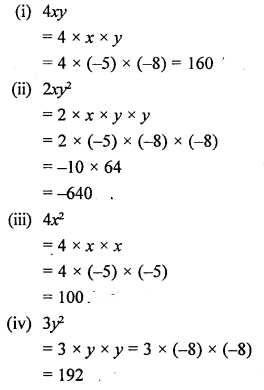
Question 28.
Find T, if T = 2a – b, a = 7 and b = 3.
Solution:
T = 2a – b, a = 1 and b = 3
Put the value of a = 1, and b = 3 in above equation
T = (2 x 7) -3
T = 14 – 3 = 11
T = 11
Question 29.
From the formula B = 2a2 – b2, calculate the value of B when a = 3 and b = -1.
Solution:
B = 2a2 – b2
Put the values of a = 3 and b = -1 in above equation
B = 2 x (3)2 – (-1)2
B = 18 – 1
B = 17
Value of B is = 17
Question 30.
The wages ₹ W of a man earning ₹ x per hour for t hours are given by the formula W = xt. Find his wages for working 40 hours at a rate of ₹ 39.45 per hour.
Solution:
T = 40 hours
x = ₹ 39.45
W = xt = 40 x 39.45
W = ₹ 1578
Question 31.
The temperature in Fahrenhiet scale is represented by F and the tempera¬ture in Celsius scale is represented by C. If F = \(\frac { 9 }{ 5 }\) x C + 32, find F when C = 40.
Solution:
F = \(\frac { 9 }{ 5 }\) x C + 32
Given, C = 40
F = \(\frac { 9 }{ 5 }\) x 40 + 32 = 9 x 8 + 32
F = 104°
Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics