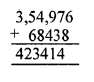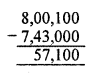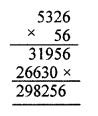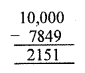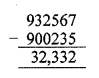Selina Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness)
Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 1 Number System (Consolidating the Sense of Numberness)
ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions
APlusTopper.com provides step by step solutions for Selina Concise ICSE Solutions for Class 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download option. Selina Publishers Concise Mathematics for Class 6 ICSE Solutions all questions are solved and explained by expert mathematic teachers as per ICSE board guidelines.
Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics
IMPORTANT POINTS
- Place-Value (Local Value) : The place value (Local-value) of a digit depends upon the position, it occupies in the number:
For example :
In the number 6453
the place value of 6 is 6 thousand = 6 x 1000 = 6000
the place value of 4 is 4 hundred = 4 x 100 = 400
the place value of 5 is 5 ten = 5 x 10 = 50
the place value of 3 is 3 one = 3 x 1 = 3 - Face-Value (True-Value) : Each digit in a number has a fixed value, regardless to its position in the number
For Example :
In the above number 6453
Face value of 6 is 6, 4 is 4, 5 is 5 and 3 is 3 - An Abstract Number : Which does not refer to any particular unit e.g., 3, 5, 9.
- A Concrete Number : Which refers to particular unit e.g., 3 boys, 5 girls, 9 rooms etc.
The smallest (least) one digit Number is 1.
The largest (greatest) one digit number is 9.
Number System Exercise 1A – Selina Concise Mathematics Class 6 ICSE Solutions
Question 1.
Which is greater ?
(i) 537 or 98
(ii) 2428 or 529
(iii) 2, 59, 467 or 10, 35, 729
Solution:
(i) 537 or 98
Since 537 is three digit number and 98 is two digit number.
Hence 537 > 98 and 537 is greater
(ii) 2428 or 529
Since 2498 is four digit number and 529 is three digit number.
2498 > 529 ; 2498 is greater
(iii) 2, 59, 467 or 10, 35, 729
Since 10, 35, 729 is seven digit number and 2, 59, 467 is six digit number
10, 35, 729 > 2, 59, 467 ; 10, 35, 729 is greater
Question 2.
Which is smaller ?
(i) 428 or 437
(ii) 2497 or 2597
(iii) 3297 or 3596
Solution:
(i) 428 or 437
We observe that both the numbers are of three-digits.
And at the leftmost, both the number have same digit i.e. 4. But at the second place from the left, the first, number has 2 and the second number has 3.
Since 2 < 3
437 is greater
(ii) 2497 or 2597
We observe that both the numbers are of four digits.
And at the leftmost, both the numbers have same digit i.e. 2. But at the second place from the left, the first number has 4 and the second number has 5.
Since 4 < 5
2597 is greater
(iii) 3297 or 3596
We observe that both the numbers are of four digits.
And at the leftmost, both the numbers have same digit i.e. 2. But at the second place from the left, the first number has 4 and the second number has 5.
Since 4 < 5
3596 is greater
Question 3.
Which is greater ?
(i) 45293 or 45427
(ii) 380362 or 381007
(iii) 63520 or 63250
Solution:
(i) 45293 or 45427
We observe that both the numbers are of 5-digits.
And at the digits at leftmost and second place from the left are same.
But the digits at the third place from the left are different, the first number has 2 and the second number has 4.
Since 2 < 4
45427 is greater
(ii) 380362 or 381007
We observe that both the numbers are of 6-digits.
And at the digits at leftmost and second place from the left are same.
But the digits at the third place from the left are different, the first number has 0 and the second number has 1.
Since 0 < 1
381007 is greater
(iii) 63520 or 63250
We observe that both the numbers are of 5-digits.
And at the digits at leftmost and second place from the left are same.
But the digits at the third place from the left are different, the first number has 5 and the second number has 2.
Since 5 < 2
63520 is greater
Question 4.
By making a suitable chart, compare:
(i) 540276 and 369998
(ii) 6983245 and 6893254
Solution:
(i) 540276 and 369998
Clearly, both the numbers have equal number of digits i.e. 6
And at the leftmost, the first number has 5 and the second number has 3.
Since 5 > 3
540276 is greater.
(ii) 6983245 and 6893254
Clearly, both the numbers have equal number of digits i.e. 7
And at the leftmost, both have the same digit i.e. 6
And at the second place from the left, the first number has 9 and the second number has 8.
Since 9 > 8
6983245 is greater.
Question 5.
Compare the numbers written in the following table by writing them in ascending order:
| 5 | 4 | 3 | 2 | 9 | 7 | 2 |
| 2 | 3 | 1 | 0 | 6 | 2 | 9 | 3 |
| 5 | 2 | 2 | 3 | 7 | 9 | 1 |
| 2 | 3 | 1 | 8 | 2 | 6 | 3 | 4 |
| 5 | 4 | 3 | 4 | 4 | 7 | 8 | 2 |
Solution:
The given number in ascending order are as :
54344782 > 243182634 > 23106293 > 5432972> 5223791
| 5 | 4 | 3 | 4 | 4 | 7 | 8 | 2 |
| 2 | 3 | 1 | 8 | 2 | 6 | 3 | 4 |
| 2 | 3 | 1 | 0 | 6 | 2 | 9 | 3 |
| 5 | 4 | 3 | 2 | 9 | 7 | 2 |
| 5 | 2 | 2 | 3 | 7 | 9 | 1 |
Question 6.
Use table form to compare the numbers in descending order : 5,43,287; 54,82,900; 27,32,940; 43,877 ; 78,396 and 4,999
Solution:
The given numbers in descending order are as :
| | | 4 | 9 | 9 | 9 |
| | 4 | 3 | 8 | 7 | 7 |
| | 7 | 8 | 3 | 9 | 6 |
| 5 | 4 | 3 | 2 | 8 | 7 |
| 2 | 7 | 3 | 2 | 9 | 4 | 0 |
| 5 | 4 | 8 | 2 | 9 | 0 | 0 |
4, 999 < 43, 877 < 78, 396 < 5, 43, 287 < 27, 32, 940 < 54, 82, 900
Question 7.
Find the smallest and the greatest numbers in each case given below:
(i) 983, 5754, 84 and 5942
(ii) 32849, 53628, 5499 and 54909.
Solution:
(i) 983, 5754, 84 ahd 5942
Since 84 has the least number of digits.
84 is the least smallest whereas 5754 and 5942 have the maximum number of digits.
Out of 5754 and 5942, 5942 is greater.
5942 is the greatest and 84 is the smallest.
(ii) 32849, 53628, 5499 and 54909.
Since 5499 has the least number of digits.
5499 is the smallest
Whereas 54909 and 53628 have the maximum number of digits. Out of 54909 and 53628, 54909 is greater.
54909 is the greatest and 5499 is the smallest
Question 8.
Form the greatest and the smallest 4 digit numbers using the given digits without repetition
(i) 3, 7, 2 and 5
(ii) 6, 1, 4 and 9
(iii) 7, 0, 4 and 2
(iv) 1, 8, 5 and 3
(v) 9, 6, 0 and 7
Solution:
(i) The given digits are 3, 7, 2 and 5
(a) The greatest 4-digit number = 7532
(b) and the smallest 4-digit number = 2357
(ii) The digits are given : 6, 1, 4 and 9
(a) The greatest 4-digit number = 9641
(b) and the smallest 4-digit number = 1469
(iii) The digits are given 7, 0, 4 and 2
(a) The greatest 4-digit number = 7420
(b) The smallest 4-digit number = 2047
(iv) the digits are given 1, 8, 5 and 3
(a) The greatest 4-digit number = 8531
(b) and the smallest 4-digit number =1358
(v) The digits are given 9, 6, 0 and 7
(a) The greatest 4-digit number = 9760
(b) and the smallest 4-digit number = 6079
Question 9.
Form the greatest and the smallest 3-digit numbers using any three different digits with the condition that digit 6 is always at the unit (one’s) place.
Solution:
The condition for 3-digit number of three different digits is that 6 is at the ones place
The greatest 3-digit number will be 986 and the smallest 3-digit number will be 106
Question 10.
Form the greatest and the smallest 4-digit number using any four different digits with the condition that digit 5 is always at ten’s place.
Solution:
The condition for 4-digit number of four different digits is that 5 is always at its tens place
The greatest 4-digit number will be 9857 and the smallest 4-digit number will be 1052
Question 11.
Fill in the blanks :
(i) The largest number of 5-digit is …………… and the smallest number of 6-digit is …………….
(ii) The difference between the smallest number of four digits and the largest number of three digits = …………. – ………….. = …………..
(iii) The sum (addition) of the smallest number of three digit and the largest number of two digit = ………… + …………= ………….
(iv) On adding one to the largest five digit number, we get ……………. which is the smallest ……………… digit number.
(v) On subtracting one from the smallest four digit number, we get ……………… which is the ……………. three digit number.
Solution:
(i) The largest number of 5-digit is 99999 and the smallest number of 6-digit is 100000
(ii) The difference between the smallest number of four digits and the largest number of three digits = 1000 – 999 = 1
(iii) The sum (addition) of the smallest number of three digit and the largest number of two digit = 100 + 99 = 199
(iv) On adding one to the largest five digit number, we get 100000 which is the smallest six digit number.
(v) On subtracting one from the smallest four digit number, we get 999 which is the greatest three digit number.
Question 12.
Form the largest number with the digits 2, 3, 5, 9, 6 and 0 without repetition of digits.
Solution:
Largest number = 9, 65, 320.
Question 13.
Write the smallest and the greatest numbers of 4 digits without repetition of any digit.
Solution:
Smallest 4 digits number = 1023
Greatest number of 4 digits = 9876
Question 14.
Find the greatest and the smallest five digit numbers with 8 in hundred’s place and with all the digits different.
Solution:
Greatest 5-digit number = 97865 and smallest 5-digit number = 10823
Question 15.
Find the sum of the largest and the smallest four-digit numbers:
Solution:
Largest four-digits number = 9,999
Smallest four digits number = 1,000
Sum of the above = 9, 999 + 1,000 = 10,999.
Question 16.
Find the difference between the smallest and the greatest six-digits numbers.
Solution:
Greatest six-digits number = 9, 99, 999
Smallest six-digits number = 1,00,000
Difference between greatest and smallest = 9, 99, 999 – 1, 00, 000 = 8, 99, 999
Question 17.
(i) How many four digit numbers are there between 999 and 3000 ?
(ii) How many four digit numbers are there between 99 and 3000 ?
Solution:
(i) Four digit numbers between 999 and 3000 = 2999 – 999 = 2000
(ii) Four digit numbers between 99 and 3000 = 2999 – 999 = 2000
Question 18.
How many four digit numbers are there between 500 and 3000 ?
Solution:
Four digits numbers between 99 and 3000 = 2999 – 999 = 2000
Question 19.
Write all the possible three digit numbers using the digits 3, 6 and 8 only; if the repetition of digits is not allowed.
Solution:
All the three digits number using 3, 6, and 8 when repetition is not allowed, can be :
368, 386, 638, 683, 836, 863.
Question 20.
Make the greatest and the smallest 4-digit numbers using the digits 5, 4, 7 and 9 (without repeating the digits) and with the condition that:
(i) 7 is at unit’s place.
(ii) 9 is at ten’s place
(iii) 4 is at hundred’s place
Solution:
(i) 7 is at unit’s place
The smallest 4-digit number using the digits 5, 4, 7 and 9, and keeping 7 at unit’s place = 4597
The greatest 4-digit number using the digits 5, 4, 7 and 9 and keeping 7 at unit’s place = 9547
(ii) 9 is at ten’s place
The smallest 4-digit number using the digits 5, 4, 7 and 9 and keeping 9 at ten’s place = 4597
The greatest 4-digit number using the digits 5, 4, 7 and 9 and keeping 9 at ten’s place = 7594
(iii) 4 is at hundred’s place
The smallest 4-digit number using the digits 5, 4, 7 and 9 and keeping 4 at hundred’s place = 5479
The greatest 4-digit number using the digits 5, 4, 7 and 9 and keeping 4 at hundred’s place = 9475
Number System Exercise 1B – Selina Concise Mathematics Class 8 ICSE Solutions
Question 1.
Population of a city was 3, 54, 976 in the year 2014. In the year 2015, it was found to be increased by 68, 438. What was the population of the city at the end of the year 2015?
Solution:
Population of a city in 2014 = 3,54, 976
Population increased in 2015 = 68, 438
Total population at the end of the year 2015 = 3, 54, 976 + 68, 438 = 423414
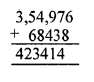
Question 2.
A = 7,43,000 and B = 8,00,100. Which is greater A or B ? And, by how much?
Solution:
A = 7,43,000
B = 8,00,100
B is greater than A. (B > A)
Because = B – A
Since A = 7, 43, 000 and B = 800,100 and both the numbers have 6 digits.
And at the leftmost, the first number has 7 and the second number has 8.
Since 8 > 7
800, 600 > 7,43,000 (B > A)
B is greater than A by = 800, 100 – 7, 43, 000 = 57, 100
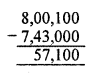
Question 3.
A small and thin notebook has 56 pages. How many total number of pages will 5326 such note-books have?
Solution:
Number of pages in one notebook = 56 pages
Number of pages in 5326 notebooks = 5326 x 56 = 298256 pages
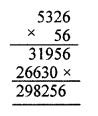
Question 4.
The number of sheets of paper available for making notebooks is 75,000. Each sheet makes 8 pages of a notebook. Each notebook contains 200 pages. How many notebooks can be made from the available paper ?
Solution:
Number of sheets available = 75, 000
Number of pages obtained from one sheet = 8
Total number of pages obtained = 8 x 75, 000 = 6, 00, 000

Question 5.
Add 1, 76, 209; 4, 50, 923 and 44, 83, 947
Solution:
1, 76, 209 + 4, 50, 923 + 44, 83, 947

Adding these values, we get = 51, 11, 079
Question 6.
A cricket player has so far scored 7, 849 runs in test matches. He wishes to complete 10, 000 runs ; how many more runs does he need ?
Solution:
Score of cricket player = 7, 849 runs
Total scores he wish to complete = 10,000
Runs required = 10, 000 – 7, 849 = 2151
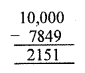
Question 7.
In an election two candidates A and B are the only contestants. If candidate A scored 9, 32, 567 votes and candidates B scored 9, 00, 235 votes, by how much margin did A win or loose the election ?
Solution:
Scores of candidate A = 9,32,567
Scores of candidate B = 9,00,235
Candidate A win the election By margin = 9,32,567 – 9,00,235 = 32,332 scores
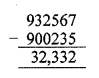
Question 8.
Find the difference between the largest and the smallest number that can be written using the digits 5, 1, 6,3 and 2 without repeating any digit.
Solution:
The digits given are = 5, 1, 6, 3 and 2
The largest 5-digit number that can be formed using the digits 5, 1, 6, 3 and 2 = 65321
The smallest 5-digit number that can be formed using the digits 5, 1,6, 37and 2 =12356
Difference between 65321 and 12356

= 65321 – 12356 = 52,965
Question 9.
A machine manufactures 5,782 screws every day. How many screws will it manufacture in the month of April ?
Solution:
Number of screws in one day = 5, 782
Number of days in April = 30 days
Number of screws in April = 5, 782 x 30 = 1,73,460

Question 10.
A man had ₹ 1, 57, 184 with him. He placed an order for purchasing 80 articles at 125 each. How much money will remain with him after the purchase ?
Solution:
Money in hand = ₹ 1, 57, 184
Number of articles purchased = 80
Cost of one article = ₹ 125
Cost of 80 articles = ₹ 80 x 125 = ₹ 10,000

Question 11.
A student multiplied 8,035 by 87 instead of multiplying by 78. By how much was his answer greater than or less than the correct answer ?
Solution:
Correct answer = 8,035 x 87 = 6,99,045

Question 12.
Mohani has 30 m cloth and she wants to make some shirts for her son. If each shirt requires 2 m 30 cm cloth, how many shirts, in all, can be made and how much length of cloth will be lefft ?
Solution:
Total length of cloth available = 30 m or 30 x 100 = 3000 cm
Shirt made by using 2m 30cm (230 cm) cloth = 1
Shirts made by using 30 m cloth = \(\frac { 1 }{ 230 }\) x 3000 = 13.04 = 13 shirts
Cloth required to make 13 shirts = 230 x 13 = 2990 cm or 29 m 90 cm
Hence, remaining cloth = 30 m – 29 m = 1m
Question 13.
The weight of a box is 4 kg 800 gm. What is the total weight of 150 boxes?>
Solution:
Weight of one box = 4 kg 800 gm
Total weight of 150 boxes = 4 kg 800 g x 150 = 720 kg

Question 14.
The distance between two places A and B is 3 km 760 m. A boy travels A to B and then B to A every day. How much distance does he travel in 8 days?
Solution:
Distance between two places = 3 km 760 m 3760 m
Distance among A to B and B to A = 2 x 3760 m = 7520 m
In 8 days he travelled = 7520 x 8 = 60160 m or 60 km 160 m
Question 15.
An oil-tin contains 6 litre 60 ml oil. How many identical bottles can the oil fill, if capacity of each bottle is 30 ml ?
Solution:
Oil contained in a tin = 6 litre 60 ml = 6 x 1000 + 60 = 6060 ml
Capacity of each bottle = 30 ml
No. of bottled can be filled with 30 ml oil = 6060 ÷ 30 = 202 bottles

Question 16.
The scale receipt of a company in a certain year was ₹ 83, 73, 540. In the following year, it was decreased by ₹ 7, 84, 670.
(i) What was the sale receipt of the company during second year?
(ii) What was the total sale receipt of the company during these two years?
Solution:
Sale receipt of the company during first year = ₹ 83,73,540
Sale decreased in second year = ₹ 7,84,670
(i) The sale receipt of the company during second year = ₹ 83,73,540 – ₹ 7,84,670
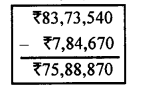
(ii) Total sale receipt of the company during these two years = ₹ 83, 73, 540 + ₹ 75, 88, 870 = ₹ 1, 59, 62, 410
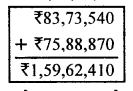
Question 17.
A number exceeds 8, 59, 470 by 3, 00, 999. What is the number?
Solution:
First number = 8, 59, 470
Difference between second and first number = 3, 00, 999
Second number = 8, 59, 470 + 3, 00, 999 = 11, 60, 469
Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics