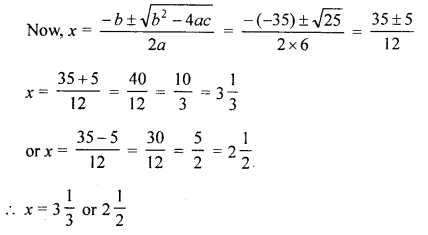Selina Concise Mathematics Class 10 ICSE Solutions Revision Paper 4
Section A (40 Marks)
(Answer all questions from this Section)
Question 1.
(a) If the sum of p terms of an A.P. is equal to sum of its q terms. Prove that the sum of (p + q) terms of it is equal to zero.
(b) Divide ₹ 1,260 among A, B and C so that the ratio between the shares of A and B is 2 : 3 and the ratio between the shares of B and C is 4 : 5.
(c) Mohan had some shares with face-value ₹ 100 paying 8% dividend. He sold them for ₹ 130 each and invested the proceed in 750 shares of some other company at ₹ 75 and paying 12% dividend. If by doing so his annual income is increased by ₹ 360, find the number of shares Mohan had.
Solution:
(a) In an A.P.
Sum of p terms = Sum of its q terms
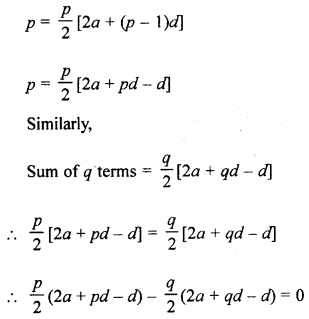
Hence sum of p + q terms will be zero,
(b) Total money = ₹ 1260
Ratio between A and B = 2 : 3
and ratio between B and C = 4 : 5
LCM of 3, 4 = 12
∴ A : B = 8 : 12
B : C = 12 : 15
∴ A : B : C = 8 : 12 : 15
Sum of ratios = 8 + 12 + 15 = 35
![]()
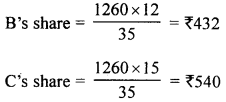
(c) Let x be the number shares
Face value of each share = ₹ 100
Rate of dividend = 8%

Question 2.
(a) The list price of an article is ₹ 6,000. A shopkeeper sells the article to a consumer at the list price and charges sales tax at 8%. If the shopkeeper pays a VAT of ₹ 64 to the state government, at what price, inclusive of sales tax, did the shopkeeper buy the article from the wholesaler ?
(b) Find the median of prime numbers between 29 and 60.
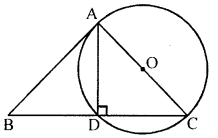
(c) The angle A of the triangle ABC is a right angle. The circle on AC as diameter cut BC at point D. If BD = 9 cm and DC = 7 cm, calculate the length of AB.
Solution:
(a) Suppose Shopkeeper purchased the article from wholesaler at ₹ x
Sales Tax paid by the shopkeeper to wholesale = \(\frac{\text { Rate of Sales Tax }}{100} \times x=\frac{8}{100} \times x\)
Selling price of Shopkeeper inclusive of VAT is ₹ 6000 and pays VAT of ₹ 64 to the state government.
VAT = Tax received by the shopkeeper from consumer – Tax paid by Shopkeeper to wholesaler
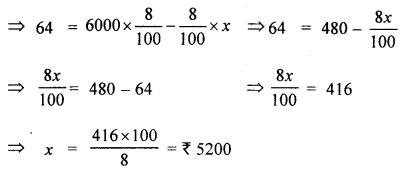
∴ The C.P. of an article for shopkeeper (exclusive of VAT) = ₹ 5200
VAT paid by the shopkeeper = 8 % of ₹ 5200 = ₹ \(\frac{8}{100}\) × 5200 = ₹ 416
∴ C.R of shopkeeper (inclusive of VAT) = ₹ (5200 + 416) = ₹ 5616
(b) Prime numbers between 29 and 60 = 31, 37, 41, 43, 47, 53, 59
There are 7 in numbers which is odd
Median =\(\frac{7+1}{2}\)th term = 4th term = 43
(c) In the figure, ∠A = 90° in ∆ABC
AC is the diameter of circle with centre O
AC cuts BC at D
BD = 9 cm, DC = 7 cm
To calculate AB
∵ AB is the tangent and BDC is a secant which intersects at B
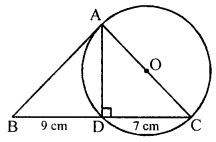
⇒ AB2 = BC × BD (By theorem)
AB2 = (9 + 7) × 9= 16 × 9= 144
AB2 = (12)2
∴ AB = 12 cm
Question 3.
(a) Govinda opened a R.D. account in a bank for 2 years 4 months. If the rate of interest is 8% per year and bank pays him ₹ 7,369.60 on maturity, find how much per month did Govinda deposit ?
(b) Given P = (x : 9 < 2x – 1 ≤ 13, x ϵ R} and Q = {x : -5 ≤ 3 + 4x < 15, x ϵ I}, where R = {real numbers} and I = {integers}. Represent P and Q on number lines. Write down the elements of P ∩ Q.
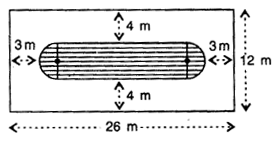
(c) Use the information given in the figure to find area of the unshaded region. Give your answer in terms of π.
Solution:
(a) Maturity value = ₹ 7369.60
Rate of interest = 8% p.a.
Period (n) = 2 years 4 months = 28 months
Let deposit per month = P
Maturity value = P × n + Interest

∴ Monthly instalment = ₹ 240
(b) P = {x : 9 < 2x – 1 ≤ 13, x ϵ R}
9 < 2x – 1 =9+ 1 < 2x ⇒ 2x > 10
\(x>\frac{10}{2}=5\)
and 2x – 1 ≤ 3 ⇒ 2x ≤ 3 + 1
⇒ 2x ≤ 4 ⇒ x ≤ \(\frac{4}{2}\)
x ≤ 2
![]()
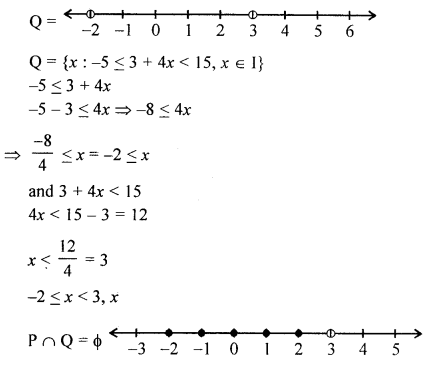
(c) Total area = l × b
= 26 m × 12 m = 312 m2
For shaded area Rectangular part
Width = b = (12 – 4 × 2) m
= (12 – 8) m = 4 m
Length = l = 26 – 2 × (3 + 2)
= (26 – 10) m= 16 m
Area of rectangular part = l × b = 16 × 4 = 64m2
Area of two semi-circular ends = \(2 \times \frac{\pi r^{2}}{2}=\pi r^{2}\)
= π(2)2 = 4πm2
∴ Total area of shaded part = (64 + 4π) m2
Thus, required area of unshaded region = [312 – (64 + 4π)] m2
= (312 – 64 – 4π) m2 = (248 – 4π) m2
Question 4.
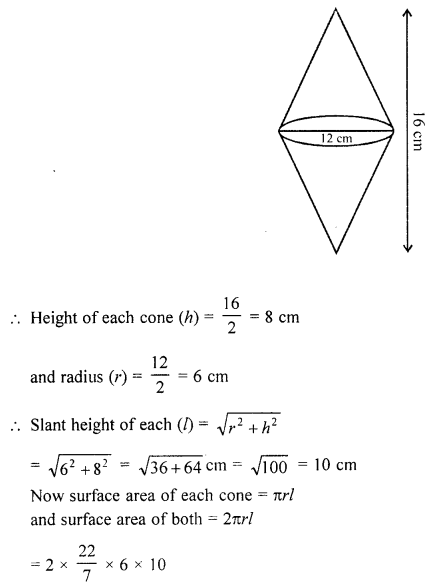
(a) Two equal cones are touching each other completely at the base circle. Given that the distance between the two vertices is 16 cm and the diameter of the base circle is 12 cm, find the total surface area of this solid.
(b) P is the solution set of : 7x – 2 > 4x + 1 and Q is the solution set of :
9x – 45 ≥ 5(x – 5); where x ϵ R,
Represent : (i) P ∩ Q, (ii) P – Q and P ∩ Q’ on different number lines.
(c) Marbles, spherical in shape, of diameter 1.4 cm are dropped into a beaker containing some water and are fully submerged. The diameter of the beaker is 7 cm. Find how many marbles have been dropped in it, if the water rises by 5.6 cm ?
Solution:
(a) Two equal cones are joined together such that their bases touch each other completely.
The total height of the figure so formed = 16 cm
and diameter of their base = 12 cm

Section B (40 Marks)
(Answer any four questions from this Section)
Question 5.
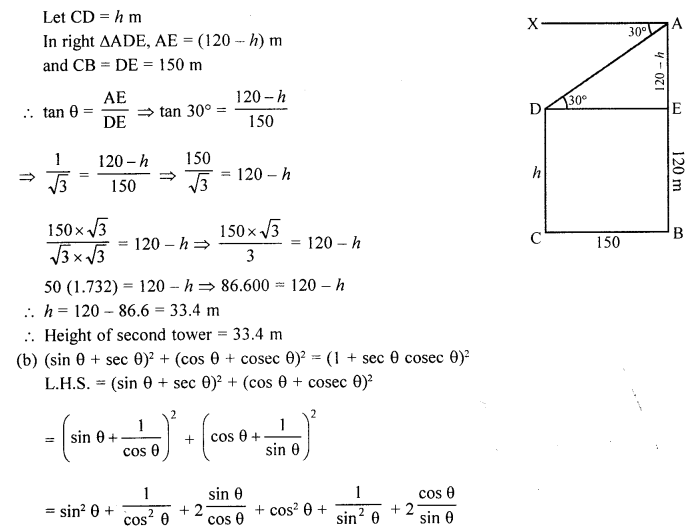
(a) The horizontal distance between two towers is 150 m. The angle of depression of the top of one tower as observed from the top of other tower, which is 120 m in height, is 30°. Find the height of the first tower.
(b) Prove that: (sin θ + sec θ)2 + (cos θ + cosec θ)2 = (1 + sec θ cosec θ)2.
(c) Find the range of values of x, which satisfy the inequality :
![]()
Graph the solution set on the number line.
Solution:
(a) Let AB and CD be the two towers
Length of AB = 120 m and
The horizontal distance between them = 150 m
The top of second tower CD, angle of depression with A is 30°
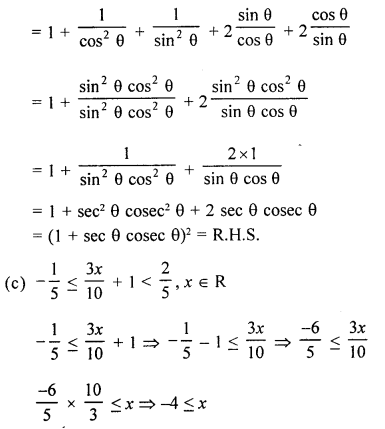
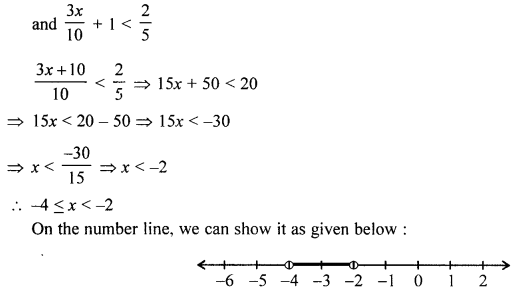
Question 6.
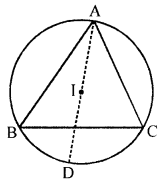
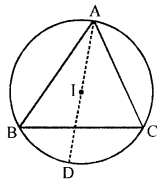
(a) In the given figure, I is the incentre of triangle ABC. AI produced meets the circumcircle of triangle ABC at point D. Given that angle ABC = 48° and angle ACB = 72°; calculate :
(i) ∠BCD
(ii) ∠CBD
(iii) ∠DCI
(iv) ∠BIC
(b) The equal chords AB and CD of a circle with centre O, when produced, meet at P outside the circle. Prove that :
(i) PB = PD
(ii) PA = PC.
(c) A man wants to buy 124 shares available at ₹ 66 (par value = ₹ 50).
(i) How much he needs to invest ?
(ii) If the dividend is 7.5%, what will be his annual income ?
(iii) If he wants to increase income by ₹ 600, how many extra shares should he buy?
Solution:
(a) In the given figure, I is the incentre of ∆ABC. AI produced meets the circumcircle of ∆ABC at D.
∠ABC = 48°, ∠ACB = 72°
To find :
(i) ∠BCD
(ii) ∠CBD
(iii) ∠DCI
(iv) ∠BIC
Construction : Join CD, BD, IC and BI
∠ABC = 48° and ∠ACB = 72°
∠BAC = 180° – (48° + 72°) = 180° – 120° = 60°
and OA is the bisector of ∠BAC
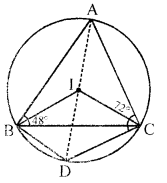
(i) Now arc BD subtends ∠BAD and ∠BCD in the same segment
∴ ∠BCD = ∠BAD = 30°
Similarly ∠CBD = ∠CAD = 30°
∠BIC = 2∠BAC = 2 × 60° = 120°
∠DCI = ∠DCB + ∠ACI = \(30^{\circ}+\frac{72^{\circ}}{2}\)
= 30° + 36° = 66°
(b) Draw OM ⊥ AB, ON ⊥ CD and join OP. Since perpendicular from the centre bisects chord.
∴ AM = BM = \(\frac{1}{2}\) AB and CN = DN = \(\frac{1}{2}\) CD
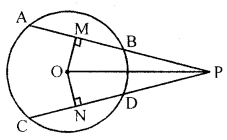
Since AB = CD (given)
⇒ AM = BM = CN = DN …(i)
In ∆OMP and ∆ONP, we have
OM = ON
(Equal chords are equidistant from the centre)
OMP = ∠ONP (each = 90°)
OP = OP (common)
∴ OMP = ONP (R.H.S.)
⇒ MP = NP (c.p.c.t.) …(ii)
(i) To prove that PB = PD
∴ MP = NP
and, BM = DN
∴ MP – BM = NP – DN
⇒ PB = PD
Hence proved.
(ii) To prove that PA = PC
∴ MP = NP [From (ii)]
and, AM = CN [From (i)]
∴ AM + MP = CN + NP
⇒ PA = PC
Hence proved.
(c) Number of shares = 124
Face value of each share = ₹ 50
and M.V. of each share = ₹ 66
(i) Investment = 124 × 66 = ₹ 8184
(ii) Rate of dividend = 7.5% = \(\frac{15}{2} \%\)
Face value of 124 shares = 124 × 50 = ₹ 6200
∴ Total dividend = \(\frac{6200 \times 15}{100 \times 2}\) = ₹ 465
(iii) For an income of ₹ 465, number of shares = 124
and for income of ₹ 600, the number of shares = \(\frac{124 \times 600}{465}\) = 160 shares
Question 7.
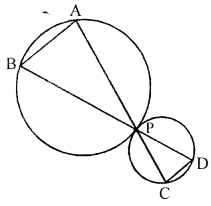
(a) Two circles touch each other externally at point P. APC and BPD are straight lines. Show that :
(i) ∆PAB and ∆PCD are similar
(ii) AB is parallel to CD.
(b) Sixteen glass spheres each of radius 2 cm are packed into a rectangular box of internal dimensions 16 cm × 8 cm × 8 cm and then the box is completely fdled with water. Find the volume of water filled in the box.
(c) The point P divides the join of (2, 1) and (-3, 6) in the ratio 2 : 3. Does P lie on the line x – 5y + 15 = 0 ?
Solution:
(a) In the given figure, two circles touch each other externally at point P. APC and BPD are straight lines.
To prove :
(i) ∆PAB and ∆PCD are similar
(ii) AB || CD
Construction : Through P, draw a common tangent to the circle.
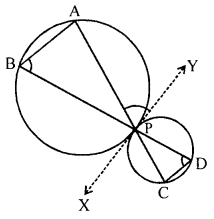
Proof: ∵ XY is tangent
∴ ∠APY = ∠B
Similarly ∠CPX = ∠D
But ∠APY = ∠CPX
∴ ∠B = ∠D
Now in ∆PAB and ∆PCD
∠B = ∠D
∠APB = ∠CPD
∴ ∆PAB ~ ∆PCD
∵ ∠B = ∠D
But there are alternate angles.
∴ AB || CD
(b) Radius of each spheres (r) = 2 cm
= 1024 – 536.38 cm3 = 487.62 cm3
(c) Point P divides the line joining the points (2, 1), (-3, 6) in the ratio 2 : 3
Let co-ordinates of P be (x, y)
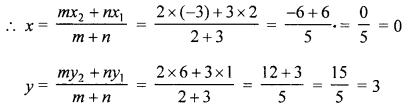
∴ Co-ordinates of P are (0, 3)
Substituting the value of x and y in the equation
x – 5y + 15 = 0
L.H.S. 0 – 5 × 3 + 15
= 0 – 15 + 15 = 0 = R.H.S.
Hence point P lies on the given line x – 5y+ 15 = 0
Question 8.
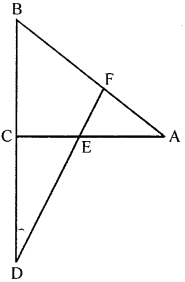
(a) In the given figure, line-segment DF intersects the side AC of a triangle ABC at point E such that E is the mid-point of CA and ∠AEF = ∠AFE.
Prove that: BD : CD = BF : CE
(b) Find the common ratio of an infinite GP. whose each term is ten times the sum of all its succeeding terms.
(c) A dividend of 9% was declared on ?100 shares selling at a certain price. If the rate of return is 7.5%, calculate :
(i) the market value of the shares.
(ii) the amount to be invested to obtain an annual dividend of ₹ 1,260.
Solution:
(a) In the given figure, line segment DF intersects the side AC of ∆ABC at E such that E is the mid-point of CA and ∠AEF = ∠AFE
To prove : BD : CD = BF : CE
Construction : Draw CG || DF
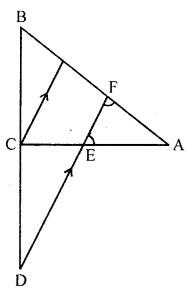
In ∆BDF
CG || DF
∴ \(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{BF}}{\mathrm{GF}}\) ……(i)
∵ ∠AEF = ∠AFE (given)
∴ AF=AE [∵ E is mid-point of CA]
∴ AF = CE
∵ In ∆CGA, CG || DF
and E is mid-point of CA
∴ F is mid-point of AG
∴ GF = CE
∴ In (i),
\(\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{BF}}{\mathrm{GF}} \Rightarrow \frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{BF}}{\mathrm{CE}} \quad(\because \mathrm{GF}=\mathrm{CE})\)
⇒ BD : CD = BF : CE
(b) In an infinite G.P., each term is ten times the sum of all its succeeding terms. Let a be first term and r be common ratio
G.P. is a, ar, ar2, ar3,
According to the condition,
a = 10(ar + ar2 + ar3) = 10ar(1 + r + r2 + ….)
\(a=10 a r\left(\frac{1}{1-r}\right) \Rightarrow a(1-r)=10 a r\)

Question 9.
(a) A circle, with centre O, circumscribes a pentagon ABCDE. If AB = BC = CD and ∠BCD = 126°, find :
(i) ∠AEB
(ii) ∠AED
(iii) ∠AOC
(b) The hotel bill for a number of persons for overnight stay is ₹ 4,800. If there were four more persons, the bill each person had to pay would have reduced by ₹ 200. Find the number of persons staying overnight.
(c) Show that any four vertices of a regular pentagon form a cyclic quadrilateral.
Solution:
A circle with centre O circumscribed a pentagon ABCDE in which
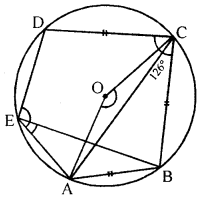
AB = BC = CD, ∠BCD = 126°
To find : (i) ∠AEB, (ii) ∠AED, (iii) ∠AOC
Join AC, BE, AO, OC
∵ AB = BC = CD and ∠BCD = 126°
∴ ∠ABC = 126°
In ∆ABC, ∠ABC = ∠BCD =126° .
∴ \(\angle \mathrm{BAC}=\angle \mathrm{BCA}=\frac{180^{\circ}-126^{\circ}}{2}=\frac{54^{\circ}}{2}=27^{\circ}\)
∠AEB and ∠ACB are in the same segment
∴ ∠AEB = ∠ACB = 27°
∵ EBCD is a cyclic quad.
∴ ∠BCD + ∠AED = 180° ⇒ 126° + ∠BED = 180°
⇒ ∠BED = 180°- 126° = 54°
∴ ∠AED = ∠AEB + ∠BED = 27° + 54° = 81°
Arc AEDC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle Reflex ∠AOC = 2 × ∠ABC = 2 × 126° = 252°
∠AOC = 360° – 252° = 108°
(b) Hotel’s bill for overnight = ₹ 4800
Let number of persons = x
∴ Each share = ₹ \(\frac{4800}{x}\)
If there are 4 more persons, then Total number of persons = x + 4
and each shares = \(\frac{4800}{x+4}\)
According to the condition,
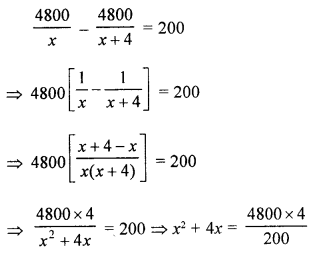
⇒ x2 + 4x – 96 = 0
⇒ x2 + 12x – 8x – 96 = 0
⇒ x(x + 12) – 8(x + 12) = 0
⇒ (x+ 12) (x – 8) = 0
Either x + 12 = 0, then x = -12 which is not possible being negative, or x – 8 = 0, then x = 8 number of persons.
(c) ABCDE is a regular pentagon
Sum of angles = 540°
∴ Each angle = \(\frac{540}{5}=108^{\circ}\)
By joining AD
∆AED is an isosceles triangle
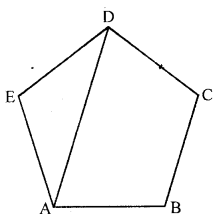
∠EAD = ∠EDB = \(\frac{180^{\circ}-108^{\circ}}{2}=\frac{72^{\circ}}{2}=36^{\circ}\)
∴ ∠ADC = 108°- 36° = 72°
Now in quad. ABCD,
∠B + ∠ADC = 108° + 72° = 180°
But these are opposite angles of an quadrilateral
∴ ABCD is a cyclic quadrilateral.
Question 10.
(a) If cosec θ – sin θ = m and sec θ – cos θ = n, then show that (m2n)2/3 + (mn2)2/3= 1.
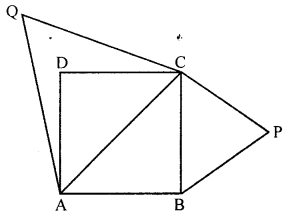
(b) Prove that the area of the equilateral triangle described on the side of a square is half the area of equilateral triangle described on its diagonals.
(c) Find the mean of the following data :
| Marks obtained: | Less than 0 | Less than 10 | Less than 20 | Less than 30 | Less than 40 | Less than 50 |
| No. of students: | 0 | 7 | 19 | 32 | 42 | 50 |
Solution:
(a) cosec θ – sin θ = m, sec θ – cos θ = n
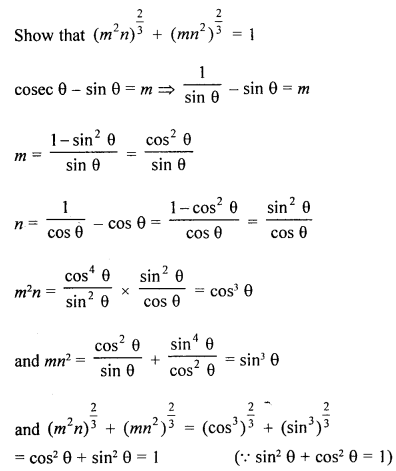
(b) Given : ABCD is a square and AC is its diagonal. Construct a equilateral triangles BCP and ACQ on side BC of square and diagonal AC.
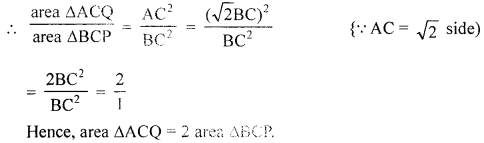
(c)
| Less than 0 | c.f | Frequency (f) | Mid value (x) | f.x. |
| 0-10 | 7 | 7 | 5 | 35 |
| 10-20 | 19 | 12 | 15 | 180 |
| 20-30 | 32 | [ 5 | 25 | 325 |
| 30-40 | 42 | ],; | 35 | 350 |
| 40-50 | 50 | 8 | 45 | 360 |
| Total | 50 | 1250 |
∴ Mean = \(\frac{\sum f x}{\Sigma f}=\frac{1250}{50}=25\)
Question 11.
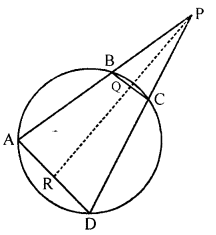
(a) In the given figure, PR is tlie bisector of ∠BPC. It meets BC and AD at point Q and R respectively. Prove that :
(i) ∠ARQ = ∠BQR
(ii) ∠ARQ + ∠RQC = 180°
(b) Construct a triangle PQR, in which PR = 6 cm and PQ = QR = 6.8 cm.
(i) Mark S the mid-point of PQ.
(ii) Construct the circle which touches QR at R and passes through S.
(c) Solve using formula : 6x2 – 35x + 50 = 0
Solution:
(a) Given : PR is bisector of ∠BPC which meets BC at Q and AD in R.
To prove : (i) ∠ARQ = ∠BQR
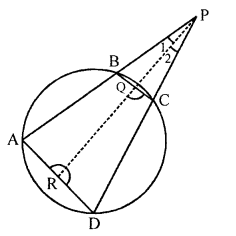
(ii) ∠ARQ + ∠RQC = 180°
Proof: (i) In ∆ARP, we have
ext. ∠DRP = ∠A + ∠1
But ∠A = ∠QCP and ∠1 = ∠2 [∵ PQ is bisector of ∠BPC]
⇒ ∠DRP = QCP + ∠2
⇒ 180°- ∠ARQ = ∠RQC
⇒ 180° – ∠ARQ =180°- ∠BQR
⇒ ∠ARQ = ∠BQR.
Hence proved.
(ii) Adding ∠RQC to both sides, we have
∠ARQ + ∠RQC
= ∠BQR + ∠RQC = 180°
Hence proved.
(b) In ∆PQR, PR = 6 cm
PQ = QR = 6.8 cm
S is mid-point of PQ
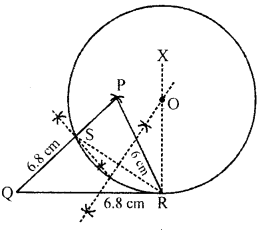
(i) Draw a line segment QR = 6.8 cm.
(ii) With Q and R as centres, draw arcs of radii 6.8cm and 6 cm respectively which intersect at P.
(iii) Join PQ and PR to form APQR.
(iv) Bisect PQ at S and join SR.
(v)Draw right bisector YZ of SR and also XR ⊥ QR, so that both intersect at O.
(vi) With O as centre and radius OS, draw a circle which passes through S and R. This circle touches QR at R.
(c) 6x2 – 35x + 50 = 0
Here, a = 6, b = -35, c = 50
b2 – 4ac = (-35)2 – 4 × 6 × 50
= 1225- 1200 = 25