ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 10 Lines and Angles Ex 10.2
Question 1.
Identity each of the given pair of angles as alternate interior angles, co-interior angles or corresponding angles or none of these in the given figure:
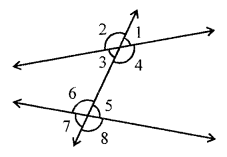
(i) ∠2, ∠6
(ii) ∠1, ∠6
(iii) ∠3, ∠5
(iv) ∠2, ∠7
(v) ∠3, ∠6
(vi) ∠4, ∠8
Solution:
In the given figure,
(i) ∠2 and ∠6 – are corresponding angles.
(ii) ∠1 and ∠6 – none
(iii) ∠3 and ∠5 – alternate interior angles
(iv) ∠2 and ∠7 – none
(v) ∠3 and ∠6 – co-interior angles
(vi) ∠4 and ∠8 – corresponding angles
Question 2.
State the property that is used in each of the following statements:
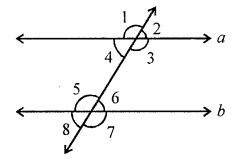
(i) If a || b, then ∠1 = ∠5.
(ii) If ∠4 = ∠6, then a || b.
(iii) If ∠4 + ∠5 = 180°, then a || b.
Solution:
In the given figure,
(i) If a || b, then
∠1 = ∠5 (Property of the corresponding pair of angles)
(ii) If ∠4 = ∠6
Property of interior alternate angles are equal
a || b
(iii) If ∠4 + ∠5 = 180°
Property of co-interior angles are supplementary, then a || b.
Question 3.
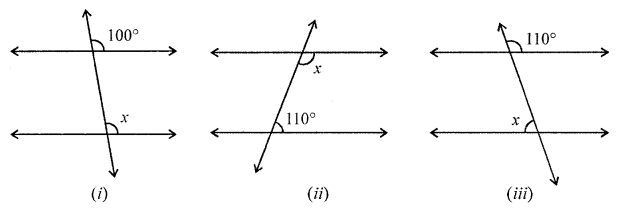
In each of the following figures, a pair of parallel lines is cut by a transversal. Find the value of x:
Solution:
(i) In the given figure,
x = 100 (Corresponding angles)
(ii) x + 110° = 180°
(Cointerior Angles are Supplementary)
x = 180° – 110° = 70°
(iii) Let ∠1 opposite to ∠110°
∠1 = 110° (Vertically opposite angles)
and ∠1 + x = 180°
(Cointerior Angles are Supplementary)
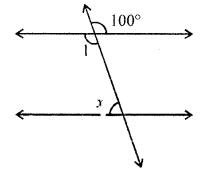
⇒ 110° + x = 180°
⇒ x = 180° – 110°
⇒ x = 70°
Question 4.
In the following figures, a pair of parallel lines are cut by a transversal. Find the value of x in each figure.
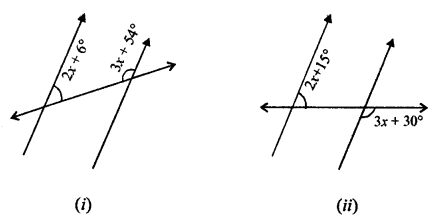
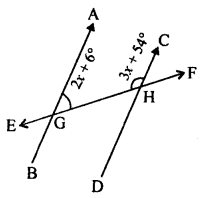
Solution:
(i) AB || CD and EF its transversal
⇒ ∠AGH + ∠GHC = 180°
⇒ 2x + 60 + 3x + 54° = 180°
(Sum of co-interior angles)
⇒ 5x + 60° = 180°
⇒ 5x = 180° – 60° = 120°
⇒ x = 24°
x = 24°
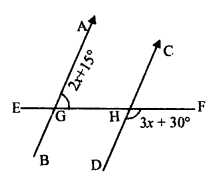
(ii) AB || CD and EF is its transversal
Which intersects them at G and H.
∠HGB = ∠FHD (Corresponding angles)
∠HGB = 3x + 30°
But ∠AGH + ∠HGB = 180° (Linear pair)
2x+ 15° + 3x + 30° = 180°
⇒ 5x + 45° = 180°
⇒ 5x = 180° – 45° = 135°
⇒ 5x = 135°
⇒ x = 27°
x = 27°
Question 5.
In the following figures (i) to (vi), a pair of parallel lines are cut by a transversal. Find the size of each lettered angle.
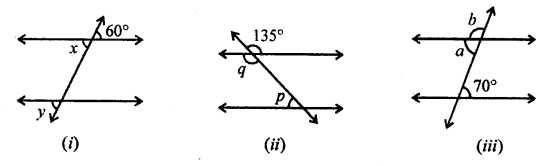
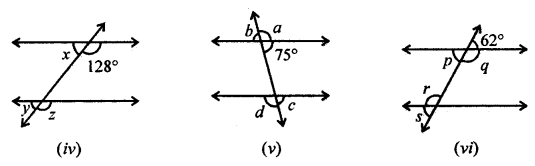
Solution:
In the given figure,
(i) Given angle is 60°
x = 60° (Vertically opposite angles)
But ∠y = ∠x (corresponding angles)
∠y = 60°
Hence, ∠x = 60°, ∠y = 60°
(ii) In the given figure,
Given angle is 135°
∠q = 135° (Vertically opposite angles)
But ∠p + ∠q = 180° (Sum of cointerior angles)
135° + ∠q = 180°
∠q = 180° – 135° = 45°
∠p = 45,°, ∠q = 135°
(iii) In the given figure,
Given angle is 70°
a = 70° (Alternate angles)
But ∠a + ∠b = 180° (Linear pair)
70° + ∠b = 180°
∠b = 180° – 70° = 110°
∠a = 70°, ∠b = 110°
(iv) In the given figure,
Given angle is 128°
∠x + 128° = 180° (Linear pair)
∠x = 180° – 128° = 52°
But ∠x = ∠y (Corresponding angles)
∠y = 52°
Also, y + z = 180° (Linear pair)
52° + ∠z = 180°
∠z = 180° – 52°
∠z = 128°
Hence, x = 52°, y = 52°, z = 128°
(v) In the given figure,
Given angle is 75°
∠a + 75° = 180° (Linear pair)
∠a = 180° – 75° = 105°
∠b = 75° (Vertically opposite angles)
∠c = 75° (Corresponding angles)
But ∠c + ∠d = 180° (Linear pair)
75° + ∠d = 180°
∠d = 180° – 75° = 105°
∠a = 105°, ∠b = 75°, ∠c = 75°, ∠d = 105°
(vi) Given angle = 62°
62 ° + ∠q = 180° (Linear pair ∠s)
∠q = 180° – 62° = 118°
∠p = 62° (Vertically opposite ∠s)
∠s = p (Corresponding ∠s)
∠s = 62°
∠s + ∠r = 180° (Linear pair ∠s)
62° + ∠r = 180°
∠r = 180° – 62° = 118°
Question 6.
In the given diagram, lines AB, CD and EF are parallel. Calculate the values of x and y. Hence, find the reflex angle ECA.
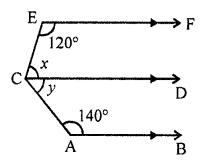
Solution:
In the given figure,
AB || CD || EF
∠E = 120°, ∠A = 140°
y + 140° = 180° (Sum of co-interior angles)
y = 180° – 140° = 40°
Similarly, x + 120° = 180°
x = 180° – 120° = 60°
x = 60°, y = 40°
Now, ∠ECA = x + y = 60° + 40° = 100°
and reflex ∠ECA = 360° – 100° = 260°
Question 7.
In the given figure, l || m. Find the values of x, y and z.
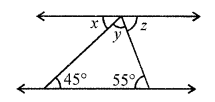
Solution:
In the given figure, x = 45° (Alternate angles)
Similarly, z = 55° (Alternate angles)
But x + y + z = 180°
(Angles on the one side of a straight line)
⇒ 45° + y + 55° = 180°
⇒ y + 100° = 180°
⇒ y = 180° – 100° = 80°
x = 45°, y = 80°, z = 55°
Question 8.
Calculate the measure of each lettered angle in the following figure (parallel lines, segment or rays are denoted by thick matching arrows):
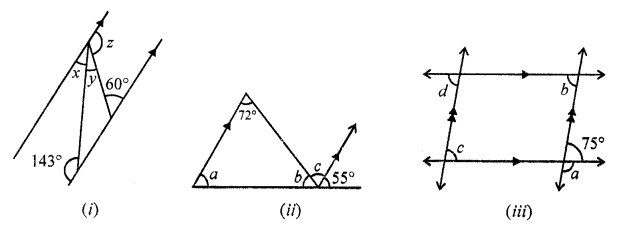
Solution:
(i) In the given figure,
∠x + 143° = 180°
(Sum of co-interior angles)
∠x = 180° – 143° = 37°
Similarly, ∠z + 60° = 180°
∠y = 180° – 60° = 120°
But ∠x + ∠y + ∠z = 180°
(Angles on one side of a straight line)
37° + 120° + ∠y = 180°
157° + ∠y = 180°
∠y = 180° – 157° = 23°
∠x = 37°, ∠y = 23°, ∠z = 120°
(ii) In the given figure,
∠c = 72° (Alternate angles)
∠a = 55° (Corresponding angles)
But ∠b + ∠c + 55° = 180°
(Angles on one side of a straight line)
∠b + 72° + 55° = 180°
∠b + 127° = 180°
∠b = 180° – 127° = 53°
Here, ∠a = 55°, ∠b = 53°, ∠c = 72°
(iii) In the given figure,
∠a + 75° = 180° (Linear pair)
∠a = 180° – 75° = 105°
∠b = 75° (Alternate angles)
∠d = b (Corresponding angles)
∠d = 75°
75° = ∠c (Corresponding angles)
∠c = 75°
∠a = 105°, ∠b = 15°, ∠c = 75°, ∠d = 75°
Question 9.
In the figure given below, state whether the lines l and m are parallel or not.
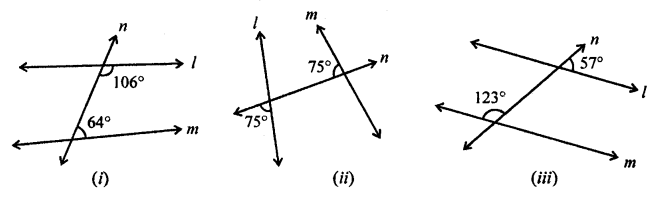
Solution:
(i) In the given figure,
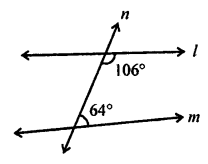
∠106° and ∠64° are co-interior angles
106° + 64° = 170°
Sum of co-interior angles is not equal to 180°
l and m are not parallel
(ii) ∠1 = 75° (Vertically opposite angles)
But ∠1 and 75° are co-interior angles
and ∠1 + 75° = 75° + 75° = 150°
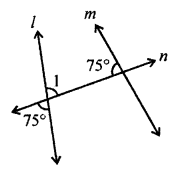
It the sum is not equal to 180°
l and m are not parallel
(ii) ∠1 = 57° (Vertically opposite angles)
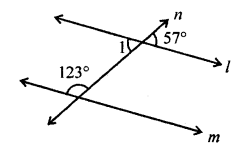
∠1 + 123° = 57° + 123° = 180° (Sum of co-interior)
∠1 + 123° = 180°
l || m