RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers
Exercise 1A
Question 1:
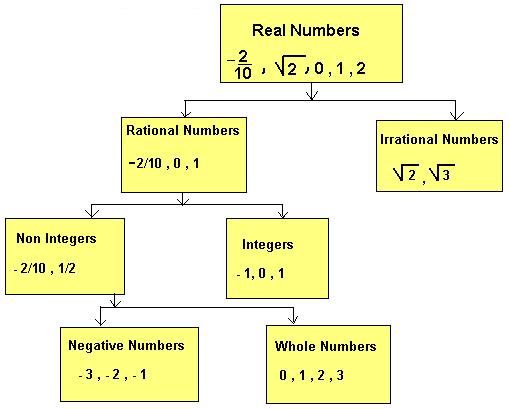
The numbers of the form \(\frac { p }{ q } \) , where p and q are integers and q ≠ 0 are known as rational numbers.
Ten examples of rational numbers are:
\(\frac { 2 }{ 3 } \), \(\frac { 4 }{ 5 } \), \(\frac { 7 }{ 9 } \), \(\frac { 8 }{ 11 } \), \(\frac { 15 }{ 23 } \), \(\frac { 23 }{ 27 } \), \(\frac { 25 }{ 31 } \), \(\frac { 26 }{ 32 } \), 1, \(\frac { 12 }{ 5 } \)
Question 2:
(i) 5
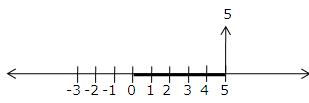
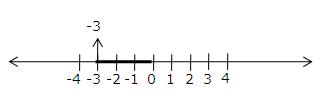
(ii) -3
(iii) \(\frac { 5 }{ 7 } \)
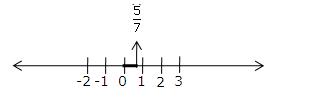
(iv) \(\frac { 8 }{ 3 } =2\frac { 2 }{ 3 } \)
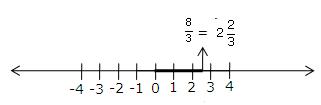
(v) 1.3
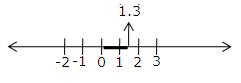
(vi) -2.4
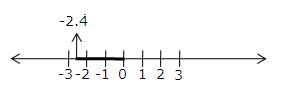
(vii) \(\frac { 23 }{ 6 } =3\frac { 5 }{ 6 } \)
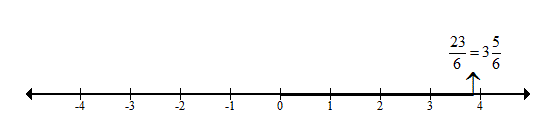
https://www.youtube.com/watch?v=HKpYfaUD-Y8
Question 3:

Question 4:
Let \(x=\frac { 1 }{ 5 } \) and \(y=\frac { 1 }{ 4 } \)
Then, x < y because \(\frac { 1 }{ 5 } \) < \(\frac { 1 }{ 4 } \)
A rational number between \(\frac { 1 }{ 5 } \) and \(\frac { 1 }{ 4 } \) is
Therefore, we have \(\frac { 1 }{ 5 } \) < \(\frac { 9 }{ 40 } \) < \(\frac { 1 }{ 4 } \)
Now, a rational number lying between \(\frac { 1 }{ 5 } \) and \(\frac { 9 }{ 40 } \) is
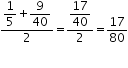
A rational number lying between \(\frac { 9 }{ 40 } \) and \(\frac { 1 }{ 4 } \) is
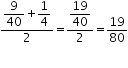
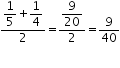
Therefore, we have \(\frac { 1 }{ 5 } \) < \(\frac { 17 }{ 80 } \) < \(\frac { 9 }{ 40 } \) < \(\frac { 19 }{ 80 } \) < \(\frac { 1 }{ 4 } \)
Or we can say that, \(\frac { 1 }{ 5 } \) < \(\frac { 17 }{ 80 } \) < \(\frac { 9\times 2 }{ 40\times 2 } \) < \(\frac { 19 }{ 80 } \) < \(\frac { 1 }{ 5 } \)
That is, \(\frac { 1 }{ 5 } \) < \(\frac { 17 }{ 80 } \) < \(\frac { 18 }{ 80 } \) < \(\frac { 19 }{ 80 } \) < \(\frac { 1 }{ 5 } \)
Therefore, three rational numbers between \(\frac { 1 }{ 5 } \) and \(\frac { 1 }{ 4 } \) are
\(\frac { 17 }{ 80 } \), \(\frac { 18 }{ 80 } \) and \(\frac { 19 }{ 80 } \)
Question 5:
Let \(x=\frac { 2 }{ 5 } \) and \(y=\frac { 3 }{ 4 } \)
Then, x < y because \(\frac { 2 }{ 5 } \) < \(\frac { 3 }{ 4 } \)
Or we can say that, \(\frac { 2\times 4 }{ 5\times 4 } =\frac { 3\times 5 }{ 4\times 5 } \)
That is, \(\frac { 8 }{ 20 } \) < \(\frac { 15 }{ 20 } \) .
We know that, 8 < 9 < 10 < 11 < 12 < 13 < 14 < 15.
Therefore, we have, \(\frac { 8 }{ 20 } \) < \(\frac { 9 }{ 20 } \) < \(\frac { 10 }{ 20 } \) < \(\frac { 11 }{ 20 } \) < \(\frac { 12 }{ 20 } \) < \(\frac { 13 }{ 20 } \)< \(\frac { 14 }{ 20 } \) < \(\frac { 15 }{ 20 } \)
Thus, 5 rational numbers between, \(\frac { 8 }{ 20 } \) < \(\frac { 15 }{ 20 } \) are:
\(\frac { 9 }{ 20 } \), \(\frac { 10 }{ 20 } \), \(\frac { 11 }{ 20 } \), \(\frac { 12 }{ 20 } \) and \(\frac { 13 }{ 20 } \)
Question 6:
Let x = 3 and y = 4
Then, x < y, because 3 < 4
We can say that, \(\frac { 21 }{ 7 } \) < \(\frac { 28 }{ 7 } \) .
We know that, 21 < 22 < 23 < 24 < 25 < 26 < 27 < 28.
Therefore, we have, \(\frac { 21 }{ 7 } \) < \(\frac { 22 }{ 7 } \) < \(\frac { 23 }{ 7 } \) < \(\frac { 24 }{ 7 } \) < \(\frac { 25 }{ 7 } \) < \(\frac { 26 }{ 7 } \)< \(\frac { 27 }{ 7 } \) < \(\frac { 28 }{ 7 } \)
Therefore, 6 rational numbers between 3 and 4 are:
\(\frac { 22 }{ 7 } \), \(\frac { 23 }{ 7 } \), \(\frac { 24 }{ 7 } \), \(\frac { 25 }{ 7 } \) and \(\frac { 26 }{ 7 } \)
Question 7:
Let x = 2.1 and y = 2.2
Then, x < y because 2.1 < 2.2
Or we can say that, \(\frac { 21 }{ 10 } \) < \(\frac { 22 }{ 10 } \)
Or, \(\frac { 21\times 100 }{ 10\times 100 } =\frac { 22\times 100 }{ 10\times 100 } \)
That is, we have, \(\frac { 2100 }{ 1000 } \) < \(\frac { 2200 }{ 1000 } \)
We know that, 2100 < 2105 < 2110 < 2115 < 2120 < 2125 < 2130 < 2135 < 2140 < 2145 < 2150 < 2155 < 2160 < 2165 < 2170 < 2175 < 2180 < 2185 < 2190 < 2195 < 2200
Therefore, we can have,
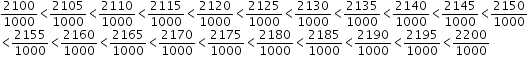
Therefore, 16 rational numbers between, 2.1 and 2.2 are:

So, 16 rational numbers between 2.1 and 2.2 are:
2.105, 2.11, 2.115, 2.12, 2.125, 2.13, 2.135, 2.14, 2.145, 2.15, 2.155, 2.16, 2.165, 2.17, 2.175, 2.18
Exercise 1B
Question 1:
(i) \(\frac { 13 }{ 80 } \)
![]()
If the prime factors of the denominator are 2 and/or 5 then the rational number is a terminating decimal.
Since, 80 has prime factors 2 and 5, \(\frac { 13 }{ 80 } \) is a terminating decimal.
(ii) \(\frac { 7 }{ 24 } \)
![]()
If the prime factors of the denominators of the fraction are other than 2 and 5, then the rational number is not a terminating decimal.
Since, 24 has prime factors 2 and 3 and 3 is different from 2 and 5,
\(\frac { 7 }{ 24 } \) is not a terminating decimal.
(iii) \(\frac { 5 }{ 12 } \)
![]()
If the prime factors of the denominators of the fraction are other than 2 and 5, then the rational number is not a terminating decimal.
Since 12 has prime factors 2 and 3 and 3 is different from 2 and 5,
\(\frac { 5 }{ 12 } \) is not a terminating decimal.
(iv) \(\frac { 8 }{ 35 } \)
![]()
If the prime factors of the denominators of the fraction are other than 2 and 5, then the rational number is not a terminating decimal.
Since 35 has prime factors 5 and 7, and 7 is different from 2 and 5,
\(\frac { 8 }{ 35 } \) is not a terminating decimal.
(v) \(\frac { 16 }{ 125 } \)
![]()
If the prime factors of the denominator are 2 and/or 5 then the rational number is a terminating decimal.
Since 125 has prime factor 5 only
\(\frac { 16 }{ 125 } \) is a terminating decimal.
Question 2:
(i)\(\frac { 5 }{ 8 } \)
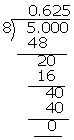
\(\frac { 5 }{ 8 } \) = 0.625
(ii) \(\frac { 9 }{ 16 } \)
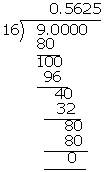
\(\frac { 9 }{ 16 } \) = 0.5625
(iii) \(\frac { 7 }{ 25 } \)
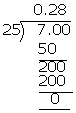
\(\frac { 7 }{ 25 } \) = 0.28
(iv)\(\frac { 11 }{ 24 } \)
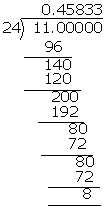
\(\frac { 11 }{ 24 } \) = 0.458\(\bar { 3 } \)
(v) \(2\frac { 5 }{ 12 } =\frac { 29 }{ 12 } \)
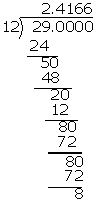
\(2\frac { 5 }{ 12 } \) = 2.41\(\bar { 6 } \)
Question 3:
(i) Let x = 0.\(\bar { 3 } \)
i.e x = 0.333 …. (i)
⇒ 10x = 3.333 …. (ii)
Subtracting (i) from (ii), we get
9x = 3
⇒ x = \(\frac { 3 }{ 9 } \) = \(\frac { 1 }{ 3 } \)
Hence, 0.\(\bar { 3 } \) = \(\frac { 1 }{ 3 } \)
(ii) Let x = 1.\(\bar { 3 } \)
i.e x = 1.333 …. (i)
⇒10x = 13.333 …. (ii)
Subtracting (i) from (ii) we get;
9x = 12
⇒ x = \(\frac { 12 }{ 9 } \) = \(\frac { 4 }{ 3 } \)
Hence, 1.\(\bar { 3 } \) = \(\frac { 4 }{ 3 } \)
(iii) Let x = 0.\(\bar { 34 } \)
i.e x = 0.3434 …. (i)
⇒ 100x = 34.3434 …. (ii)
Subtracting (i) from (ii), we get
99x = 34
⇒ x = \(\frac { 34 }{ 99 } \)
Hence, 0.\(\bar { 34 } \) = \(\frac { 33 }{ 99 } \)
(iv) Let x = 3.\(\bar { 14 } \)
i.e x = 3.1414 …. (i)
⇒ 100x = 314.1414 …. (ii)
Subtracting (i) from (ii), we get
99x = 311
⇒ x = \(\frac { 311 }{ 99 } \)
Hence, 3.\(\bar { 14 } \) = \(\frac { 311 }{ 99 } \)
(v) Let x = 0.\(\bar { 324 } \)
i.e. x = 0.324324 ….(i)
⇒ 1000x = 324.324324….(ii)
Subtracting (i) from (ii), we get
999x = 324
⇒ x = \(\frac { 324 }{ 999 } \) = \(\frac { 12 }{ 37 } \)
Hence, 0.\(\bar { 324 } \) = \(\frac { 12 }{ 37 } \)
(vi) Let x = 0.\(\bar { 17 } \)
i.e. x = 0.177 …. (i)
⇒ 10x = 1.777 …. (ii)
and 100x = 17.777…. (iii)
Subtracting (ii) from (iii), we get
90x = 16
⇒ x = \(\frac { 16 }{ 90 } \) = \(\frac { 8 }{ 45 } \)
Hence, 0.\(\bar { 17 } \) = \(\frac { 8 }{ 45 } \)
(vii) Let x = 0.\(\bar { 54 } \)
i.e. x = 0.544 …. (i)
⇒ 10 x = 5.44 …. (ii)
and 100x = 54.44 ….(iii)
Subtracting (ii) from (iii), we get
90x = 49
⇒ x = \(\frac { 49 }{ 90 } \)
Hence, 0.\(\bar { 54 } \) = \(\frac { 49 }{ 90 } \)
(vii) Let x = Let x = 0.1\(\bar { 63 } \)
i.e. x = 0.16363 …. (i)
⇒ 10x = 1.6363 …. (ii)
and 1000 x = 163.6363 …. (iii)
Subtracting (ii) from (iii), we get
990x = 162
⇒ x = \(\frac { 162 }{ 990 } \) = \(\frac { 9 }{ 55 } \)
Hence, 0.1\(\bar { 63 } \) = \(\frac { 9 }{ 55 } \)
Question 4:
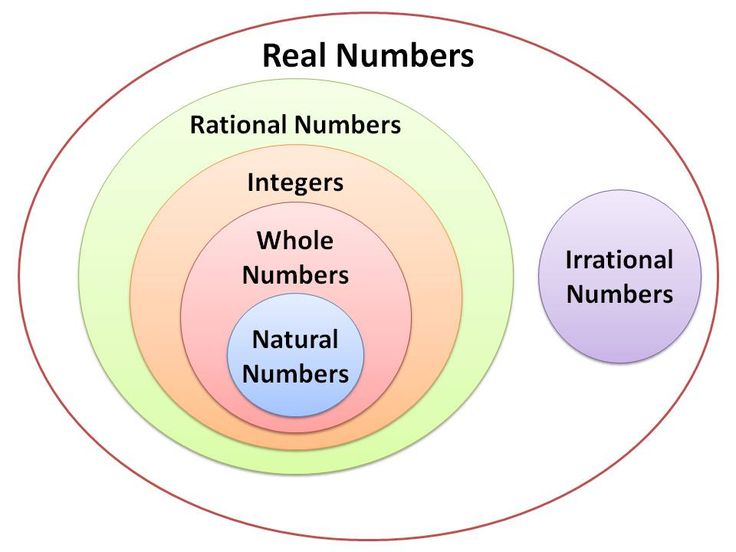
(i) True. Since the collection of natural number is a sub collection of whole numbers, and every element of natural numbers is an element of whole numbers
(ii) False. Since 0 is whole number but it is not a natural number.
(iii) True. Every integer can be represented in a fraction form with denominator 1.
(iv) False. Since division of whole numbers is not closed under division, the value of \(\frac { p }{ q } \), p and q are integers and q ≠ 0, may not be a whole number.
(v) True. The prime factors of the denominator of the fraction form of terminating decimal contains 2 and/or 5, which are integers and are not equal to zero.
(vi) True. The prime factors of the denominator of the fraction form of repeating decimal contains integers, which are not equal to zero.
(vii) True. 0 can considered as a fraction \(\frac { 0 }{ 1 } \), which is a rational number.
Exercise 1C
Question 1:
Irrational number: A number which cannot be expressed either as a terminating decimal or a repeating decimal is known as irrational number. Rather irrational numbers cannot be expressed in the fraction form, \(\frac { p }{ q } \), p and q are integers and q ≠ 0
For example, 0.101001000100001 is neither a terminating nor a repeating decimal and so is an irrational number.
Also, \(\sqrt { 2 } ,\quad \sqrt { 5 } ,\quad \sqrt { 3 } ,\quad \sqrt { 6 } ,\quad \sqrt { 7 } \) etc are examples of irrational numbers.
Question 2:
(i) \(\sqrt { 4 } \)
We know that, if n is a perfect square, then \(\sqrt { n } \) is a rational number.
Here, 4 is a perfect square and hence, \(\sqrt { 4 } \) = 2 is a rational number.
So, \(\sqrt { 4 } \) is a rational number.
(ii) \(\sqrt { 196 } \)
We know that, if n is a perfect square, then \(\sqrt { n } \) is a rational number.
Here, 196 is a perfect square and hence \(\sqrt { 196 } \) is a rational number.
So, \(\sqrt { 196 } \) is rational.
(iii) \(\sqrt { 21 } \)
We know that, if n is a not a perfect square, then \(\sqrt { n } \) is an irrational number.
Here, 21 is a not a perfect square number and hence, \(\sqrt { 21 } \) is an irrational number.
So, \(\sqrt { 21 } \) is irrational.
(iv) \(\sqrt { 43 } \)
We know that, if n is a not a perfect square, then \(\sqrt { n } \) is an irrational number.
Here, 43 is not a perfect square number and hence, \(\sqrt { 43 } \) is an irrational number.
So, \(\sqrt { 43 } \) is irrational.
(v) \(3+\sqrt { 3 } \)
\(3+\sqrt { 3 } \), is the sum of a rational number 3 and \(\sqrt { 3 } \) irrational number .
Theorem: The sum of a rational number and an irrational number is an irrational number.
So by the above theorem, the sum, \(3+\sqrt { 3 } \), is an irrational number.
(vi) \(\sqrt { 7 } -2 \)
\(\sqrt { 7 } -2 \) = \(\sqrt { 7 } \) + (-2) is the sum of a rational number and an irrational number.
Theorem: The sum of a rational number and an irrational number is an irrational number.
So by the above theorem, the sum, \(\sqrt { 7 } \) + (-2) , is an irrational number.
So, \(\sqrt { 7 } -2 \) is irrational.
(vii) \(\frac { 2 }{ 3 } \sqrt { 6 } \)
\(\frac { 2 }{ 3 } \sqrt { 6 } \) = \(\frac { 2 }{ 3 } \) × \(\sqrt { 6 } \) is the product of a rational number and an irrational number .
Theorem: The product of a non-zero rational number and an irrational number is an irrational number.
Thus, by the above theorem, \(\frac { 2 }{ 3 } \) × \(\sqrt { 6 } \) is an irrational number.
So, \(\frac { 2 }{ 3 } \sqrt { 6 } \) is an irrational number.
(viii) 0.\(\bar { 6 } \)
Every rational number can be expressed either in the terminating form or in the non-terminating, recurring decimal form.
Therefore, 0.\(\bar { 6 } \) = 0.6666
Question 3:
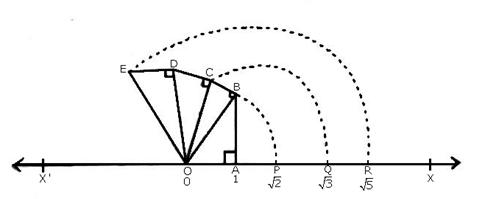
Let X’OX be a horizontal line, taken as the x-axis and let O be the origin. Let O represent 0.
Take OA = 1 unit and draw BA ⊥ OA such that AB = 1 unit, join OB. Then,
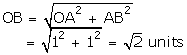
With O as centre and OB as radius, drawn an arc, meeting OX at P.
Then, OP = OB = \(\sqrt { 2 } \) units
Thus the point P represents \(\sqrt { 2 } \) on the real line.
Now draw BC ⊥ OB such that BC = 1 units
Join OC. Then,
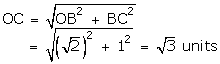
With O as centre and OC as radius, draw an arc, meeting OX at Q. The,
OQ = OC = \(\sqrt { 3 } \) units
Thus, the point Q represents \(\sqrt { 3 } \) on the real line.
Now draw CD ⊥ OC such that CD = 1 units
Join OD. Then,
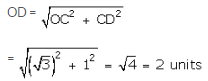
Now draw DE ⊥ OD such that DE = 1 units
Join OE. Then,
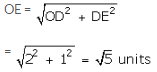
With O as centre and OE as radius draw an arc, meeting OX at R.
Then, OR = OE = \(\sqrt { 5 } \) units
Thus, the point R represents \(\sqrt { 5 } \) on the real line.
Question 4:
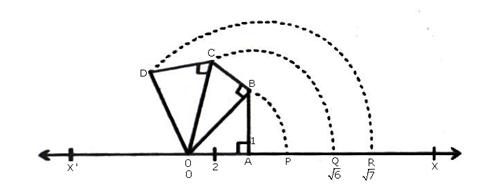
Draw horizontal line X’OX taken as the x-axis
Take O as the origin to represent 0.
Let OA = 2 units and let AB ⊥ OA such that AB = 1 units
Join OB. Then,
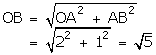
With O as centre and OB as radius draw an arc meeting OX at P.
Then, OP = OB = \(\sqrt { 5 } \)
Now draw BC ⊥ OB and set off BC = 1 unit
Join OC. Then,
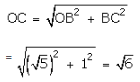
With O as centre and OC as radius, draw an arc, meeting OX at Q.
Then, OQ = OC = \(\sqrt { 6 } \)
Thus, Q represents \(\sqrt { 6 } \) on the real line.
Now, draw CD ⊥ OC as set off CD = 1 units
Join OD. Then,
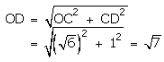
With O as centre and OD as radius, draw an arc, meeting OX at R. Then
OR = OD = \(\sqrt { 7 } \)
Thus, R represents \(\sqrt { 7 } \) on the real line.
Question 5:
(i) \(4+\sqrt { 5 } \)
Since 4 is a rational number and \(\sqrt { 5 } \) is an irrational number.
So, \(4+\sqrt { 5 } \) is irrational because sum of a rational number and irrational number is always an irrational number.
(ii) \((-3+\sqrt { 6 } ) \)
Since – 3 is a rational number and \(\sqrt { 6 } \) is irrational.
So, \((-3+\sqrt { 6 } ) \) is irrational because sum of a rational number and irrational number is always an irrational number.
(iii) \(5\sqrt { 7 } \)
Since 5 is a rational number and \(\sqrt { 7 } \) is an irrational number.
So, \(5\sqrt { 7 } \) is irrational because product of a rational number and an irrational number is always irrational.
(iv) \(-3\sqrt { 8 } \)
Since -3 is a rational number and \(\sqrt { 8 } \) is an irrational number.
So, \(-3\sqrt { 8 } \) is irrational because product of a rational number and an irrational number is always irrational.
(v) \(\frac { 2 }{ \sqrt { 5 } } \)
![]()
\(\frac { 2 }{ \sqrt { 5 } } \) is irrational because it is the product of a rational number and the irrational number \(\sqrt { 5 } \).
(vi) \(\frac { 4 }{ \sqrt { 3 } } \)
![]()
\(\frac { 4 }{ \sqrt { 3 } } \) is an irrational number because it is the product of rational number and irrational number \(\sqrt { 3 } \).
Question 6:
(i) True
(ii) False
(iii) True
(iv) False
(v) True
(vi) False
(vii) False
(viii) True
(ix) True
Exercise 1D
Question 1:
(i)
![]()
We have:
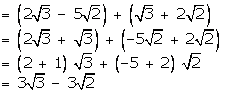
(ii)
![]()
We have:
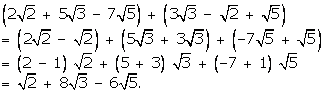
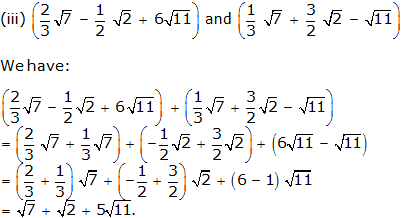
Question 2:
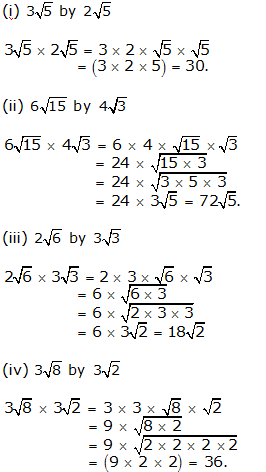
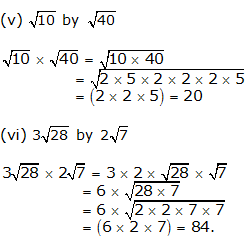
Question 3:
(i) \(16\sqrt { 6 } \) by \(4\sqrt { 2 } \)
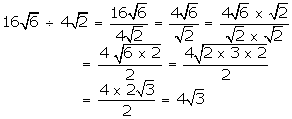
(ii) \(12\sqrt { 15 } \) by \(4\sqrt { 3 } \)
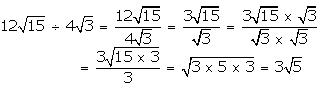
(iii) \(18\sqrt { 21 } \) by \(6\sqrt { 7 } \)
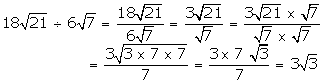
Question 4:
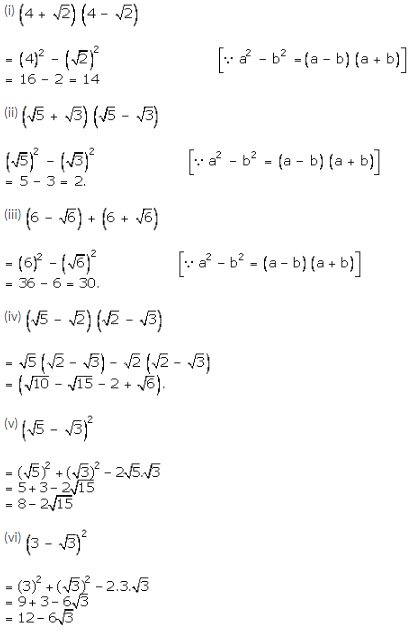
Question 5:
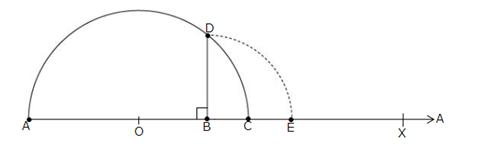
Draw a line segment AB = 3.2 units and extend it to C such that BC = 1 units.
Find the midpoint O of AC.
With O as centre and OA as radius, draw a semicircle.
Now, draw BD AC, intersecting the semicircle at D.
Then, BD = \(\sqrt { 3.2 } \) units.
With B as centre and BD as radius, draw an arc meeting AC produced at E.
Then, BE = BD = \(\sqrt { 3.2 } \) units.
Question 6:
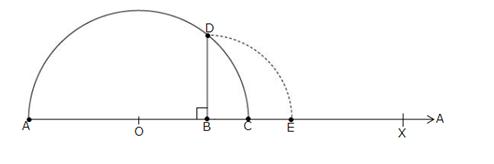
Draw a line segment AB = 7.28 units and extend it to C such that BC = 1 unit.
Find the midpoint O of AC.
With O as centre and OA as radius, draw a semicircle.
Now, draw BD AC, intersecting the semicircle at D.
Then, BD = \(\sqrt { 7.28 } \) units.
With D as centre and BD as radius, draw an arc, meeting AC produced at E.
Then, BE = BD = \(\sqrt { 7.28 } \) units.
Question 7:
Closure Property: The sum of two real numbers is always a real number.
Associative Law: (a + b) + c = a + (b + c) for al real numbers a, b, c.
Commutative Law: a + b = b + a, for all real numbers a and b.
Existence of identity: 0 is a real number such that 0 + a = a + 0, for every real number a.
Existence of inverse of addition: For each real number a, there exists a real number (-a) such that
a + (-a) = (-a) + a= 0
a and (-a) are called the additive inverse of each other.
Existence of inverse of multiplication:
For each non zero real number a, there exists a real number \(\frac { 1 }{ a } \) such that
![]()
a and \(\frac { 1 }{ a } \) are called the multiplicative inverse of each other.
Exercise 1E
Question 1:
On multiplying the numerator and denominator of the given number by \(\sqrt { 7 } \), we get
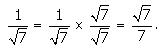
Question 2:
On multiplying the numerator and denominator of the given number by \(\sqrt { 3 } \), we get
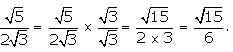
Question 3:
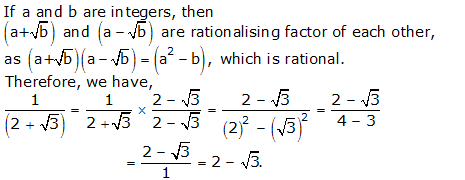
Question 4:
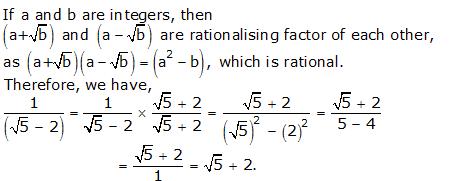
Question 5:
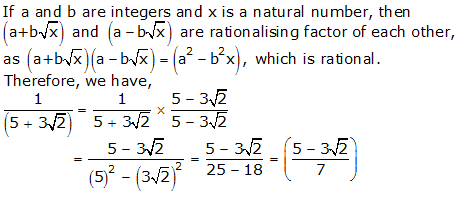
Question 6:
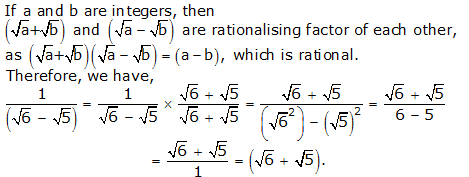
Question 7:
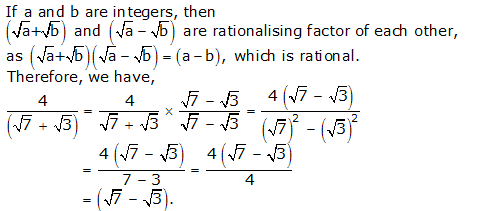
Question 8:

Question 9:

Question 10:

Question 11:

Question 12:
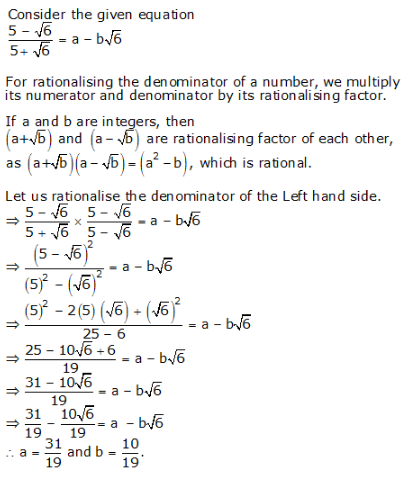
Question 13:

Question 14:

Question 15:

Question 16:
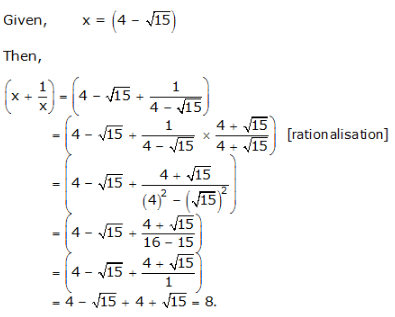
Question 17:
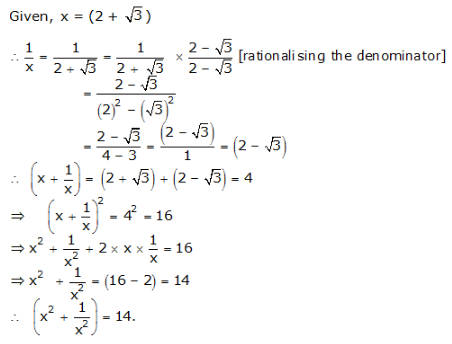
Question 18:
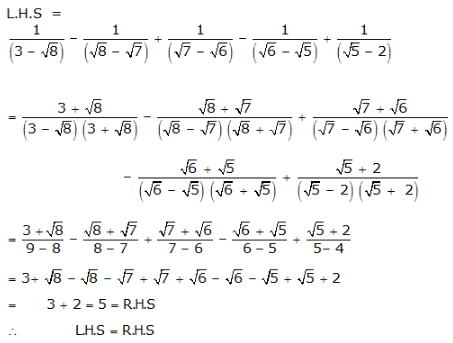
Exercise 1F
Question 1:
(i)
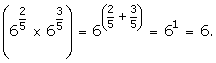
(ii)
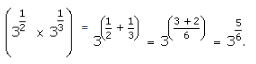
(iii)
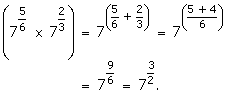
Question 2:
(i)
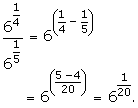
(ii)
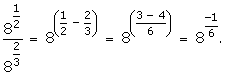
(iii)
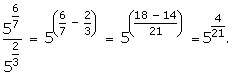
Question 3:
(i)
![]()
(ii)
![]()
(iii)
![]()
Question 4:
(i)
![]()
(ii)
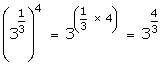
(iii)
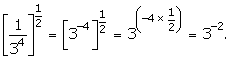
Question 5:
(i)
![]()
(ii)
![]()
(iii)
![]()
Question 6:
(i)
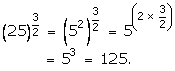
(ii)
![]()
(iii)
![]()
Question 7:
(i)

(ii)

(iii)
