ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 9 Direct and Inverse Variation Ex 9.1
Question 1.
Observe the following tables and find if x and y are directly proportional:
(i)
| x | 5 | 8 | 12 | 15 | 18 | 20 |
| y | 15 | 24 | 36 | 60 | 72 | 100 |
(ii)
| x | 3 | 5 | 7 | 9 | 10 |
| y | 9 | 15 | 21 | 27 | 30 |
Solution:
(i) x and y are in direct variation of \(\frac{x}{y}\) is constant
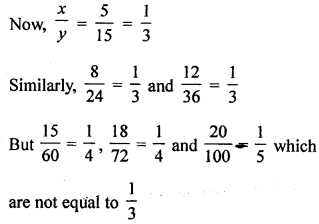
\(\frac{x}{y}\) is not constantThere are not directly proportional
(ii) \(\frac{x}{y}=\frac{3}{9}=\frac{1}{3}\)
Similarly, \(\frac{5}{15}=\frac{1}{3}, \frac{7}{21}=\frac{1}{3}, \frac{9}{27}=\frac{1}{3}\) and
\(\frac{10}{30}=\frac{1}{3}\)
∴ \(\frac{x}{y}\) is constant
Here, x and y are directly proportional.
Question 2.
If x and y are in direct variation, complete the following tables:
(i)
| x | 3 | 5 | … | 10 | |
| y | 45 | … | 90 | 120 |
(ii)
| x | 4 | 8 | … | 20 | 28 |
| y | 7 | … | 21 | … | … |
Solution:

Hence,
| x | 3 | 5 | 6 | 8 | 10 |
| y | 45 | 75 | 90 | 120 | 150 |
(ii)
| x | 4 | 8 | … | 20 | 28 |
| y | 7 | … | 21 | … | … |
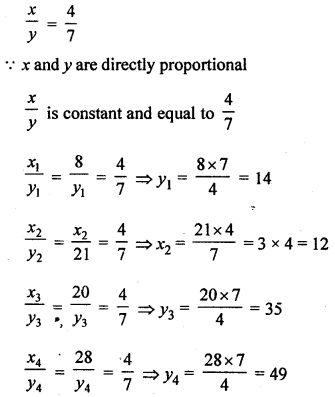
Hence
| x | 4 | 8 | 12 | 20 | 28 |
| y | 7 | 14 | 21 | 35 | 49 |
Question 3.
If 8 metres cloth costs ₹250, find the cost of 5·8 metres of the same cloth.
Solution:
Let the cost of 5·8 m cloth = ₹ x
| Length (in m) | 8 | 5.8 |
| Cost of cloth (₹) | 250 | x |
Hence, it is the case of direct variation
∴ 8 : 250 = 5.8 : x
⇒ \(\frac{8}{250}=\frac{5.8}{x}\)
⇒ \(x=\frac{5.8 \times 250}{8}\) = ₹181.25
Question 4.
If a labourer earns ₹672 per week, how much will he earn in 18 days?
Solution:
Let the labourer earns ₹ x in 18 days
| Days | 7 | 18 |
| Money earned (in ₹) | 672 | x |
Hence, it is in the case of direct variation
![]()
Question 5.
If 175 dollars cost ₹7350, how many dollars can be purchased in ₹24024?
Solution:
Let x dollars be purchased in ₹24024
| Cost (in ₹) | 7350 | 24024 |
| Dollars | 175 | x |
Hence, the question is of direct variation
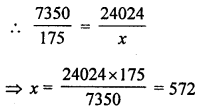
Question 6.
If a car travels 67·5 km in 4·5 litres of petrol, how many kilometres will it travel in 26.4 litres of petrol?
Solution:
Let car travels x km in 26·4 litres of petrol
| Distance (in km) | x | 67.5 |
| Petrol (in l) | 26.4 | 4.5 |
Hence, the question is of direct variation
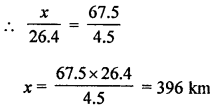
Question 7.
If the thickness of a pile of 12 cardboard sheets is 45 mm, then how many sheets of the same cardboard would be 90 cm thick?
Solution:
Thickness of 12 cardboard = 45 mm
Let x be the number of cardboard whose thickness is 90 cm = 900 m
12 : x = 45 : 900 ⇒ \(\frac{12}{x}=\frac{45}{900}\)
⇒ x = \(\frac{12 \times 900}{45}\) = 240 mm
Thickness of 90 cardboard = 240 mm
Question 8.
In a model of a ship, the mast (flagstaff) is 6 cm high, while the mast of the actual ship is 9 m high. If the length of the ship is 33 m, how long is the model of the ship?
Solution:
Height of a model of ship = 6 cm
But height of actual ship = 9 m
If length of ship = 33 m
Let length of model = x
∴ 6 : x = 9 m : 33
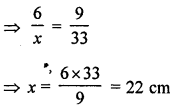
∴ Length of model = 22 cm
Question 9.
The mass of an aluminium rod varies directly with its length. If a 16 cm long rod has a mass of 192 g, find the length of the rod whose mass is 105 g.
Solution:
Length of rod = 16 cm and mass = 192 g
If mass is 105 g, then
Let length of rod = x cm
∴ 16 : x = 192 : 105
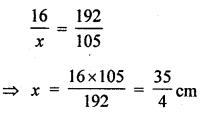
= 8.75 cm
Question 10.
Anita has to drive from village A to village B. She measures a distance of 3.5 cm between these villages on the map. What is the actual distance between the villages if the map scale is 1 cm = 20 km?
Solution:
Distance from village A to B on the map = 3.5 cm
Scale of map 1 cm = 20 km
Let actual distance = x km
∴ 1 : 3.5 = 20 : x
\(\frac{1}{3.5}=\frac{20}{x}\) ⇒ x = 20 × 3.5 km 3.5
⇒ x = 70 km
∴ Distance between village A and village B 20 km
Question 11.
A 23 m 75 cm high water tank casts a shadow 20 m long. Find at the same time;
(i) the length of the shadow cast by a tree 9 m 50 cm high.
(ii) the height of the tree if the length of the shadow is 12 m.
Solution:
Height of a water tank = 23 m 75 cm
= \(23 \frac{3}{4} m=\frac{95}{4} m\)
and its shadow = 20 m
(i) If height of a tree = 9 m 50 cm = \(9 \frac{1}{2}\) m

∴ Its shadow = 8 m
(ii) Let height of a tree = x m
and its shadow = 12 m
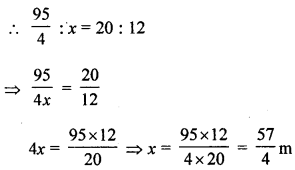
⇒ x =14 m 25 cm
∴ Height of the tree = 14 m 25 cm
Question 12.
If 5 men or 7 women can earn ₹525 per day, how much would 10 men and 13 women will earn per day.
Solution:
Since in a day, 5 men can earn ₹525
∴ In a day, 1 men can earn = ₹ \(\frac{525}{5}\) = ₹105
∴ In a day, 10 men will earn ₹105 × 10 = ₹1050
As in a day 7 women can earn ₹525
∴ In a day, 1 women can earn = ₹\(\frac{525}{7}\) = ₹75
In a day 13 women will earn ₹75 × 13 = ₹975
∴ Total earning of 7 men and 13 women in a day = ₹(1050 + 975) = ₹2025