ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 9 Direct and Inverse Variation Ex 9.2

ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 9 Direct and Inverse Variation Ex 9.2

Question 1.
Which of the following are in inverse variation?
(i) Number of students in a hostel and consumption of food.
(ii) Time taken by a train to cover a fixed distance and the speed of the train.
(iii) Area of land and its cost.
(iv) The number of people working and the time to complete the work.
(v) The quantity of rice and its cost.
Solution:
(i), (ii) and (iv) are inverse variations as here
xy = constant.

Question 2.
Observe the following tables and find which pair of variables (here x and y) are in inverse variation:

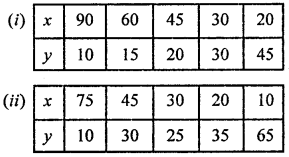
Solution:
∵ x and y are in inverse variation
∴ xy is constant
(i) Now, xy = 90 × 10 = 900
xy = 60 × 15 = 900
xy = 45 × 20 = 900
xy = 30 × 30 = 900
xy = 20 × 45 = 900
We see that in every, xy is constant.
∴ It is in inverse variation.

(ii) x × y = 75 × 10 = 750
xy = 45 × 30 = 1350
xy = 30 × 25 = 750
xy = 20 × 35 = 700
xy= 10 × 65 =650
We see that in each case xy is not same.
It is not in inverse variation.

Question 3.
Under the condition that the temperature remains constant, the volume of gas is inversely proportional to its pressure. If the volume of gas is 630 cubic centimetres at a pressure of 360 mm of mercury, then what will be the pressure of the gas, if its volume is 720 cubic centimetres at the same temperature?
Solution:
Temperature remains constant and volume of gas
is inversly proportional to its pressure,
x = Volume of gas = 630 cubic cm
y Pressure = 360 mm
Let pressure of gas be a mm
and their volume = 720 cubic cm
630 × 360 = a × 720
a = \(\frac{630 \times 360}{720}\) = 315
∴ Pressure of gas = 315 mm of mercury.

Question 4.
A packet of sweets was distributed among 20 children and each of them received 4 sweets. How many sweets will each child get, if the number of children is reduced by 4?
Solution:
x₁ = 20 and y₂ = 4
x₂ = 16 and y₂ = ?
x₁y₁ = x₂y₂
⇒ 20 × 4 = 16 × y₂
⇒ y₂ = \(\frac{20 \times 4}{16}\) = 5
Each child will get 5 sweets.

Question 5.
Pooja has enough money to buy 36 oranges at the rate of ₹4.50 per orange. How many oranges she can buy if the price of each orange is increased by 90 paise?
Solution:
Cost of one orange = ₹4.50
∴ Cost of 36 oranges = ₹4.50 × 36 = ₹162
New price of one orange = ₹ 4.50 + 0.90 = ₹5.40
∴ In ₹ 162, oranges can be bought = \(\frac{162}{5.40}\) = 30
Hence number of oranges available = 30

Question 6.
It takes 8 days for 12 men to construct a wall. How many men should be put on the job if it is required to be constructed in 6 days.?
Solution:
12 men construct a wall in 8 days.
∴ man construct a wall in = 12 × 8 days
∴ 6 men construct a wall in = \(\frac{12 \times 8}{6}\) days = 16 days

Question 7.
Eight taps through which water flows at the same rate can fill a tank in 27 minutes. If two taps go out of order, how long will the remaining taps take to fill the tank ?
Solution:
Eight taps through which water flows can fill a tank in 27 minutes.
Two taps go out of order then, reamining taps = 8 – 2 = 6
∴ taps through which w’ater flows can fill a tank in = 27 × 8 minutes
∴ 6 taps through which water flows can fill a tank in = \(\frac{27 \times 8}{6}\) minutes
= \(\frac{27 \times 4}{3}\) minutes = 36 minutes

Question 8.
A contractor undertook a contract to complete a part of a stadium in 9 months with a team of 560 persons. Later on, it was required to complete the job in 5 months. How many extra persons should he employ to complete the work?
Solution:
To complete a work, 560 persons were employed for 9 months,
but to complete the same work is to be completed in 5 months,
so person will be = \(\frac{560 \times 9}{5}\) = 1008 person
Persons already working = 560
∴ More persons to be required = 1008 – 560 = 648 persons

Question 9.
A batch of bottles were packed in 30 boxes with 10 bottles in each box. If the same batch is packed using 12 bottles in each box, how many boxes would be filled?
Solution:
A batch of bottles were packed in 30 boxes with 10 bottles in each box.
Number of boxes required to fill 12 bottles at each box = \(\frac{30 \times 10}{12}\) = 25 boxes

Question 10.
Vandana takes 24 minutes to reach her school if she goes at a speed of 5 km/h. If she wants to reach school in 20 minutes, what should be her speed?
Solution:
Vandana takes 24 minutes to reach her school with a speed of 5 km/h
To reach the school in 20 minutes, she will go with a speed = \(\frac{24 \times 5}{20}\) = 6 km/h

Question 11.
A fort is provided with food for 80 soldiers to last for 60 days. Find how long would the food last if 20 additional soldiers join after 15 days.
Solution:
After 15 days, the food is sufficient for 80 soldiers for (60 – 15) days i.e. 45 days.
After 15 days, 20 additional soldiers join the fort.
So number of soldiers in the fort = 80 + 20 = 100
Since for 80 soldiers, the food is sufficient for = 45 days
∴ For 1 soldiers, the food is sufficient for = (80 × 45) days
∴ For 100 soldiers, the food is sufficient for = \(\frac{80 \times 45}{100}\) days = 36 days.

Question 12.
1200 soldiers in a fort had enough food for 28 days. After 4 days, some soldiers were sent to another fort and thus, the food lasted for 32 more days. How many soldiers left the fort?
Solution:
Number of total days = 28
Days spent = 4
∴ No. of days left = 28 – 4 = 24
No. of soldiers = 1200
and the food lasted for = 32 days
∴ In 24 days, the food is sufficient for = 1200 soldiers
In 1 day, the food will be sufficient for = 1200 × 24
and in 32 days, the food will be sufficient for = \(\frac{1200 \times 24}{32}\) = 900 persons
∴ No. of soldiers sent to another fort = 1200 – 900 = 300

ML Aggarwal Class 8 Solutions for ICSE Maths