Math Labs with Activity – Find the Circumcentre of a Given Triangle

by

Math Labs with Activity – Find the Circumcentre of a Given Triangle

OBJECTIVE

To find the circumcentre of a given triangle by the method of paper folding.

Materials Required

  1. Three sheets of white paper
  2. A geometry box

Theory
The point of intersection of the perpendicular bisectors of the sides of a triangle is called its circumcentre.

Procedure
Step 1: We shall first find the circumcentre of an acute- angled triangle. Draw an acute-angled triangle ABC on a sheet of white paper.
Step 2: Fold the paper along the line that cuts the side BC such that the point B falls on the point C. Make a crease and unfold the paper. Draw a line X1Y1 along the crease. Then, X1Y1 is the perpendicular bisector of the side BC (see Figure 19.1).
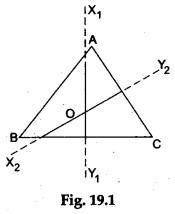
Math Labs with Activity - Find the Circumcentre of a Given Triangle 1
Step 3: Fold the paper along the line that cuts the side AC such that the point A falls on the point C. Make a crease and unfold the paper. Draw a line X2Y2 along the crease. Then X2Y2 is the perpendicular bisector of the side AC (see Figure 19.1). Mark the point O where the lines X1Y1 and X2Y2 intersect. Then, the point O is the circumcentre of ΔABC. What do you observe?
Step 4: We shall now find the circumcentre of a right-angled triangle. Draw a right-angled triangle ABC (right angled at C) on another sheet of white paper.
Step 5: Fold the paper along the line that cuts the side BC such that the point B falls on the point C. Make a crease and unfold the paper. Draw a line X1Y1 along the crease. Then, X1Y1 is the perpendicular bisector of the side BC (see Figure 19.2).
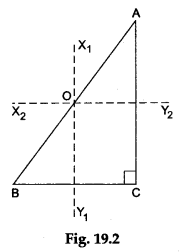
Math Labs with Activity - Find the Circumcentre of a Given Triangle 2
Step 6: Fold the paper along a line that cuts the side AC such that the point A falls on the point C. Make a crease and unfold the paper. Draw a line X2Y2 along the crease. Then, X2Y2 is the perpendicular bisector of the side AC (see Figure 19.2). Mark the point O where the lines X1Y1 and X2Y2 intersect. Then, O is the circumcentre of ΔABC. What do you observe?
Step 7: We shall now find the circumcentre of an obtuse¬angled triangle. Draw an obtuse-angled triangle ABC (in which ∠B is obtuse) on the third sheet of white paper.
Step 8: Fold the paper along the line that cuts the side BC such that the point B falls on the point C. Make a crease and unfold the paper. Draw a line X1Y1 along the crease. Then, X1Y1 is the perpendicular bisector of the side BC (see Figure 19.3).
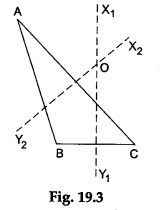
Math Labs with Activity - Find the Circumcentre of a Given Triangle 3
Step 9: Fold the paper along the line that cuts the side AC such that the point A falls on the point C. Make a crease and unfold the paper. Draw a line X2Y2 along the crease. Then, X2Y2 is the perpendicular bisector of the side AC (see Figure 19.3). Mark the point O where the lines X1Y1 and X2Y2 intersect. Then, O is the circumcentre of ΔABC. What do you observe?

Observations

  1. In an acute-angled triangle, the circumcentre lies inside the triangle.
  2. In a right-angled triangle, the circumcentre lies at the midpoint of the hypotenuse. This can be confirmed by drawing the perpendicular bisector of the hypotenuse. The three perpendicular bisectors meet at the midpoint of the hypotenuse.
  3. In an obtuse-angled triangle, the circumcentre lies outside the triangle.

Result
The point O is the circumcentre of the triangle (in each case).

Remarks: The teacher must explain it to the students that since the perpendicular bisectors of all the three sides of a triangle meet at a single point, it is sufficient to find the point of intersection of the perpendicular bisectors of only two sides to obtain the circumcentre of the triangle.

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills

Leave a Comment