Math Labs with Activity – Derive a Formula for Finding the Area of a Parallelogram

by

Math Labs with Activity – Derive a Formula for Finding the Area of a Parallelogram

OBJECTIVE

To derive a formula for finding the area of a parallelogram.

Materials Required

  1. Two sheets of white paper
  2. A sheet of glazed paper
  3. A geometry box
  4. A tube of glue
  5. A pair of scissors

Theory
It has been geometrically proved that the area of a parallelogram having base =b units and height =h units is given by area =(b x h) square units.

Procedure
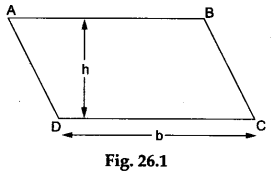
Step 1: Construct a parallelogram ABCD having base=b units and height =h units on a sheet of white paper as shown in Figure 26.1.
Math Labs with Activity - Derive a Formula for Finding the Area of a Parallelogram 1
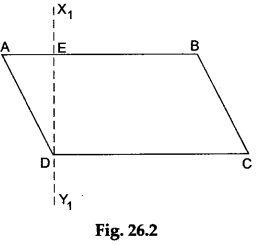
Step 2: Make an exact copy of the parallelogram ABCD on the glazed paper. Fold the glazed paper along the line that passes through the point D and cuts the side AB such that the part of the line AB that lies on one side of the line of fold falls on the other part. Make a crease and unfold the paper. Draw a line X1Y1 along the line of fold. Mark the point E where X1Y1 cuts the side AB as shown in Figure 26.2.
Math Labs with Activity - Derive a Formula for Finding the Area of a Parallelogram 2
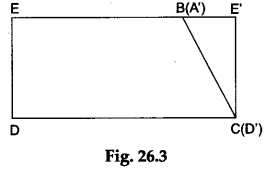
Step 3: Cut the ΔAED and the quadrilateral EBCD. Label the triangle as ΔA’E’D’. Paste the quadrilateral EBCD and the  ΔA’E’D’ on a new sheet of white paper as shown in Figure 26.3.
Math Labs with Activity - Derive a Formula for Finding the Area of a Parallelogram 3
Step 4: Record your observations.

Observations and Calculations
We observe that a rectangle is formed when the two parts of the parallelogram are arranged as shown in Figure 26.3.
Length of the rectangle DCE’E =DC =b units (from Figure 24.1). Breadth of the rectangle DCE’E=ED = h units.
area of the rectangle DCE’E = (b x h) square units.
Hence, the area of the parallelogram ABCD = (b x h) square units.

Result
The area of a parallelogram is equal to the product of its base and height.

Remarks: The teacher must discuss the case where the perpendicular falls outside the base as shown in Figure 26.4.
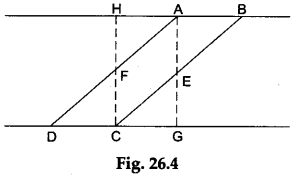
Math Labs with Activity - Derive a Formula for Finding the Area of a Parallelogram 4
ABCD is a parallelogram in which the perpendicular from the point A falls outside the base DC. In such a case we drop a perpendicular AG from the point A on the side DC (produced) and another perpendicular CH from the point C on the side AB (produced). Mark the points E and F where the perpendiculars AG and CH intersect the sides BC and AD respectively. Cut  ΔDEC and place it over ΔCEG. Also, cut ΔABE and place it over ΔHAF. We thus get a rectangle HAGC whose area is given by area =AB x AG.
So, area of the given parallelogram = AB x AG =base x height.

Math Labs with ActivityMath LabsMath Lab ManualScience LabsScience Practical Skills

Leave a Comment