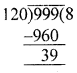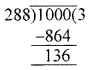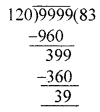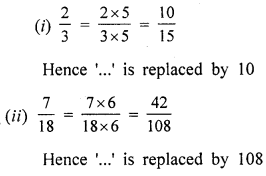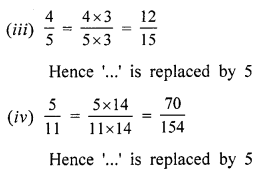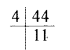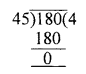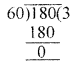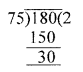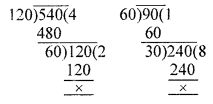ICSE

ML Aggarwal Class 7 Solutions for ICSE Maths Chapter 15 Visualising Solid Shapes Objective Type Questions

Mental Maths

Question 1.
Fill in the blanks:
(i) A solid having no vertex and no edge is a ………..
(ii) A solid that has congruent and parallel polygons as top and bottom faces and all other faces rectangular is known as ………
(iii) A pyramid having 4 equilateral triangles as its faces is known as ………
(iv) A solid having 3 faces (one curved and two circulars), no vertex and two curved edges are known as ……..
(v) A solid having a circular base and one vertex is called a ………
(vi) A triangular prism has ……… faces, ………… edges and ………. vertices.
(vii) A triangular pyramid has ……… faces, ………. edges and ……… vertices.
(viii) A square pyramid has ……… faces, ……….. edges and ……… vertices.
(ix) The base of a triangular pyramid is a ………
(x) Out of ……….. faces of a triangular prism, ……… are rectangle and ……….. are triangles.
(xi) Out of ……….. faces of a square pyramid, ………. are a triangle and ………. is/are squares.
(xii) Out of ………. faces of a rectangular pyramid, ………. are triangles and the base is a ……….
(xiii) A ……….. is a sort of skeleton – outline in 2-D, which on folding results in a 3-D shape.
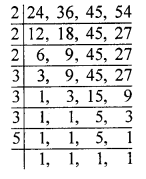
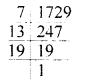
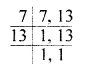
(xiv) If the sum of numbers on the two dice thrown together is 9, then the sum of the numbers opposite to these faces is ……….
Solution:
(i) A solid having no vertex and no edge is a sphere.
(ii) A solid that has congruent and parallel polygons as top and bottom faces
and all other faces rectangular is known as a prism.
(iii) A pyramid having 4 equilateral triangles as its faces is known as a tetrahedron.
(iv) A solid having 3 faces (one curved and two circulars),
no vertex and two curved edges are known as a cylinder.
(v) A Solis’having a circular base and one vertex is called a cone.
(vi) A triangular prism has 5 faces, 9 edges, and 6 vertices.
(vii) A triangular pyramid has 4 faces, 6 edges, and 4 vertices.
(viii) A square pyramid has 5 faces, 8 edges, and 5 vertices.
(ix) The base of a triangular pyramid is a triangle.
(x) Out of 5 faces of a triangular prism, 3 are rectangle and 2 are triangles.
(xi) Out of 5 faces of a square pyramid, 4 are triangle and 1 is/are squares.
(xii) Out of 5 faces of a rectangular pyramid, 4 are triangles and the base is a rectangle.
(xiii) A net is a sort of skeleton – outline in 2-D, which on folding results in a 3-D shape.
(xiv) If the sum of numbers on the two dice thrown together is 9,
then the sum of the numbers opposite to these faces is 5.

Question 2.
State whether the following statements are true (T) or false (F):
(i) The faces of a prism are triangular.
(ii) A cube can be treated as a prism.
(iii) A pyramid has only one vertex.
(iv) All the faces, except the base, of a square pyramid are triangular.
(v) A tetrahedron has 3 rectangular faces and 1 rectangle face.
(vi) A square pyramid has 5 faces and one vertex.
(vii) A cone has one vertex, two faces, and one curved edge.
(viii)The shadow of a 3-D object is a 2-D figure.
(ix) A cube can cast a shadow in the shape of a rectangle.
(x) A cube can cast a shadow in the shape of a hexagon.
(xi) In an isometric sketch, the line segments of different lengths can represent the sides of a cube.
(xii) In an oblique sketch of a cuboid, the size of the opposite faces must be different.
(xiii) The top, front and side views of a sphere are different.
(xiv) The adjoining net is of a hexagonal pyramid.

Solution:
(i) The faces of a prism are triangular. (False)
Correct:
Faces are rectangular.
(ii) A cube can be treated as a prism. (True)
(iii) A pyramid has only one vertex. (False)
Correct:
It has three or more than three.
(iv) All the faces, except the base, of a square pyramid are triangular. (True)
(v) A tetrahedron has 3 rectangular faces and 1 rectangle face. (False)
Correct:
It has triangular faces.
(vi) A square pyramid has 5 faces and one vertex. (False)
Correct:
It has five vertices, not one.
(vii) A cone has one vertex, two faces, and one curved edge. (True)
(viii) The shadow of a 3-D object is a 2-D figure. (True)
(ix) A cube can cast a shadow in the shape of a rectangle. (True)
(x) A cube can cast a shadow in the shape of a hexagon. (False)
(xi) In an isometric sketch, the line segments of different lengths
can represent the sides of a cube. (False)
Correct:
A cube has equal length.
(xii) In an oblique sketch of a cuboid, the size of the opposite faces
must be different. (False)
(xiii) The top, front and side views of a sphere are different. (False)
Correct:
All are equal.
(xiv) The adjoining net is of a hexagonal pyramid. (True)

Multiple Choice Questions

Choose the correct answer from the given four options (3 to 11):
Question 3.
A triangular prism has
(a) 4 vertices and 6 edges
(b) 6 vertices and 9 edges
(c) 6 vertices and 6 edges
(d) 9 vertices and 6 edges
Solution:
A triangular prism has 6 vertices and 9 edges. (b)

Question 4.
A square pyramid has
(a) 4 vertices and 4 faces
(b) 4 vertices and 5 faces
(c) 5 vertices and 4 faces
(d) 5 vertices and 5 faces
Solution:
A square pyramid has 5 vertices and 5 faces. (d)

Question 5.
A solid having 4 (plane) faces, 4 vertices and 6 edges is called a
(a) triangular prims
(b) rectangular prism
(c) triangular pyramid
(d) rectangular pyramid
Solution:
A solid having 4 (plane) faces,
4 vertices and 6 edges is called rectangular pyramid. (c)

Question 6.
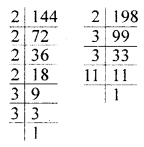
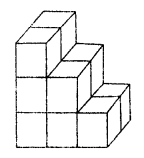
The number of cubes in the given structure is
(a) 12
(b) 10
(c) 9
(d) 8

Solution:
The number of cubes in the given structure is 12. (a)

Question 7.
An isometric sheet is made up of dots forming
(a) squares
(b) rectangles
(c) right-angled triangles
(d) equilateral triangles
Solution:
An isometric sheet is made up of dots
forming equilateral triangles. (d)

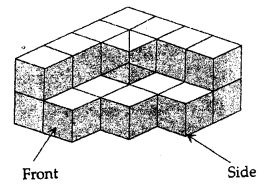
Question numbers 8 to 11 are based on the given figure in which unit cubes are put together to form a structure as shown:

Question 8.
The number of unit cubes in the given structure is
(a) 13
(b) 20
(c) 21
(d) 22
Solution:
The number of unit cubes in the given structure is 21. (c)

Question 9.
The number of unit cubes to be added to make a cuboid of dimensions 4 unit × 4 unit × 2 unit is
(a) 11
(b) 12
(c) 13
(d) 14
Solution:
The number of unit cubes to be added to make a cuboid of dimensions
4 unit × 4 unit × 2 unit is 4 × 4 × 2 = 32 – 21 = 11 (a)

Question 10.
If the structure is painted on the surface everywhere, then the number of unit cubes having no face painted is
(a) 0
(b) 1
(c) 2
(d) 11
Solution:
If the structure is painted on the surface everywhere,
then the number of unit cubes ‘ having no face painted is 1. (b)

Question 11.
The side view of the given structure is

Solution:
The side view of the given structure is (c).

ML Aggarwal Class 7 Solutions for ICSE Maths

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Ex 4.5

Question 1.
Find the L.C.M. of the given numbers by prime factorisation method :
(i) 28, 98
(ii) 36, 40, 126
(iii) 108, 135, 162
(iv) 24, 28, 196.
Solution:
(i) Prime factorisation of the given numbers are:
28 = 2 × 2 × 7
98 = 2 × 7 × 7
Here 2 and 7 occurs as a prime factor maximum 2 times
∴ L.C.M. = 2 × 2 × 7 × 7 = 196

(ii) Prime factorisation of the given numbers are:
36 = 2 × 2 × 3 × 3
40 = 2 × 2 × 2 × 5
126 = 2 × 3 × 3 × 7
Notice that 2 occurs as a prime factor maximum 3 times, 3 two times, 5 one times and 7 one times
∴ L.C.M. = 2 × 2 × 2 × 3 × 3 × 5 × 7
= 2520

(iii) Prime factorisation of given umbers are
108 = 2 × 2 × 3 × 3 × 3
135 = 3 × 3 × 3 × 5
162 = 2 × 3 × 3 × 3 × 3
Notice that 2 occurs as a prime factor
maximum 2 times, 3, four time and 5, one time
∴ L.C.M.= 2 × 2 × 3 × 3 × 3 × 3 × 5 = 1620

(iv) Prime factorisation of the given numbers are
24 = 2 × 2 × 2 × 3
28 = 2 × 2 × 7
196 = 2 × 2 × 7 × 7
Notice that 2 occurs as a prime factor maximum 3 times, 3 one times, 7 two times
∴ L.C.M. = 2 × 2 × 2 × 3 × 7 × 7 = 1176

Question 2.
Find the L.C.M. of the given numbers by division method :
(i) 480, 672
(ii) 6, 8, 45
(iii) 24, 40, 84
(iv) 20, 36, 63, 67
Solution:
(i) 480, 672

∴ L.C.M. = 2 × 2 × 2 × 2 × 2 × 3 × 5 × 7 = 3360

(ii) 6, 8, 45

∴ LCM = 2 × 2 × 2 × 3 × 3 × 5 = 360

(iii) 24, 40, 84

∴ LCM = 2 × 2 × 2 × 3 × 5 × 7 = 840

(iv) 20, 36, 63, 97

∴ L.C.M. = 2 × 2 × 3 × 3 × 5 × 7 × 11 = 13860

Question 3.
Find the least number which when increased by 15 is exactly divisible by 15, 35 and 48.
Solution:
First, we find the least number which is exactly divisible by the numbers 15, 35 and 48. For this, we find L.C.M. of 15, 35 and 48.

∴ L.C.M. = 3 × 5 × 7 × 2 × 2 × 2 × 2 = 1680
According to given condition, the required number will be 15 less than 1680.
∴ The required least number = 1680- 15 = 1665

Question 4.
Find the least number which when divided by 6, 15 and 18 leaves remainder 5 in each case.
Solution:
LCM of 6, 15 and 18

= 2 × 3 × 3 × 5 = 90
Hence, the required number is 90 + 5 i.e. 95 48

Question 5.
Find the least number which when divided by 24, 36, 45 and 54 leaves a remainder of 3 in each case.
Solution:
24, 36, 45 and 54

∴ L.C.M. = 2 × 2 × 2 × 3 × 3 × 3 × 5 = 1080
According to given condition, the required number will be 3 more than 1080.
∴ The required number = 1080 + 3 = 1083

Question 6.
Find the greatest 3-digit number which is exactly divisible by 8, 20 and 24.
Solution:
First, we find the LCM of 8, 20 and 24

∴ LCM of given numbers = 2 × 2 × 2 × 3 × 5 = 120
Greatest number of 3 digit is 999
We divide 999 by 120 and find the remainder.

According to given condition, we need a greatest 3-digit number which is exactly divisible by 120.
∴ The required number = 999 – 39 = 960

Question 7.
Find the smallest 4-digit number which is exactly divisible by 32, 36 and 48.
Solution:
First, we find the LCM of 32, 36 and 48

∴ LCM of given number
= 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288
Smallest number of 4-digit = 1000
We divide 1000 by 288 and find the remainder

According to given condition, we need a least number of 4-digit which is exactly divisible by 288.
∴ The required number = 1000 + (288 – 136) = 1152

Question 8.
Find the greatest 4-digit number which is exactly divisible by each of 8, 12 and 20.
Solution:
First, we find the LCM of 8, 12 and 20

∴ LCM of given numbers = 2 × 2 × 2 × 3 × 5 = 120
According to given condition, we need a greatest number of 4-digit which is exactly divisible by 120.
Greatest number of 4-digit = 9999
We divide 9999 by 120 and find the remainder

∴ The required number = 9999 – 39 = 9960

Question 9.
Find the least number of five digits which is exactly divisible by 32, 36 and 45.
Solution:
First we, find the LCM of 32, 36 and 45

∴ LCM of given numbers
= 2 × 2 × 2 × 2 × 2 × 3 × 3 × 5 = 1440
Smallest 5-digit number = 10000
We divided 10000 by 1440 and find the remainder

According to given condition,
We need a least 5-digit number which is exactly divisible by 1440
The required number
= 10000 + 1440 – 1360
= 10080

Question 10.
Three boys step off together from the same spot. Their steps measure 63 cm, 70 cm and 77 cm respectively. What is the minimum distance each should cover so that all can cover the same distance in complete steps?
Solution:
The L.C.M. of 63, 70 and 77

⇒ 63 = 3 × 3 × 7
70 = 2 × 5 × 7
77 = 7 × 11
∴ L.C.M. = 3 × 3 × 2 × 5 × 7 × 11 = 6930
∴ The minimum distance each shall cover is 6930 cm i.e. 69 m 30 cm

Question 11.
Traffic lights at three different road crossing change after 48 seconds, 72 seconds and 108 seconds respectively. At what time will they change together again if they change simultaneously at 7 A.M.?
Solution:
LCM of 48, 72 and 108

= 2 × 2 × 2 × 2 × 3 × 3 × 3 = 432
432 seconds = 7 minutes 12 seconds past 7 A.M.

Question 12.
If the product of two numbers is 4032 and their HCF is 12, find their LCM.
Solution:
Product of two number = 4032
H.C.F = 12
L.C.M = 4032 ÷ 12 = 336

Question 13.
The HCF and LCM of two numbers are 9 and 270 respectively. If one of the numbers is 45, find the other number.
Solution:
HCF × LCM = one number × 2nd number
9 × 270 = 45 × 2nd number.
2430 = 45 × 2nd number
2430 = 45 × 2nd number
\(=\frac{2430}{45}=\frac{162}{3}=54\)
∴ 54 is other number.

Question 14.
Find the HCF of 180 and 336. Hence, find their LCM.
Solution:
Division method: HCF of 180 and 336

∴ H.C.R of 180 and 336 = 12
Products of numbers LCM of 180 and 336= \(\frac{\text { Products of numbers }}{\text { their H.C.F. }}\)
\(=\frac{180 \times 336}{12}=15 \times 336=5040\)

Question 15.
Can two numbers have 15 as their HCF and 110 as their LCM? Give reason to justify your answer.
Solution:
On dividing 110 by 15, we get

7 as quotient and 5 as remainder
We find that the remainder ≠ 0
So 110 is not exactly divisible by 15
∴ HCF and L.C.M. of two numbers cannot be 15 and 110 respectively.
As LCM of two numbers is always exactly divisible by their HCF.

ML Aggarwal Class 6 Solutions for ICSE Maths

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 6 Fractions Ex 6.3

Question 1.
State which of the following fractions are proper, improper or mixed:

Solution:

Question 2.
Convert the following improper fractions into mixed numbers:

Solution:

Question 3.
Convert the following mixed number into improper fractions:


Solution:

Question 4.
Write the fractions representing the shaded regions. Are all these fractions equivalent?

Solution:

Yes, all the fractions are equivalent.

Question 5.
Write the fractions representing the shaded regions and pair up the equivalent fractions from each row:


Solution:

Equivalent fractions are:
(i) ↔ (d)
(ii) ↔ (b)
(iii) ↔ (e)
(iv) ↔ (a)
(v) ↔ (c)

Question 6.
(i) Find the equivalent fraction of \(\frac{15}{35}\) with denominator 7.
(ii) Find the equivalent fraction of \(\frac{2}{9}\) with denominator 63.
Solution:
(i) \(\frac{15}{35}=\frac{ . . .}{7}\)
Let the numerator be a
⇒ 15 × 7 = 35 × a
\(a=\frac{15 \times 7}{35}\)
⇒ a = 3
∴ \(\frac{15}{35}=\frac{3}{7}\)

(ii) \(\frac{2}{9}=\frac{\dots}{63}\)
Let the numerator, which needs to be calculated as x
⇒ 2 × 63 = 9 × x
⇒ \(x=\frac{2 \times 63}{9}\)
⇒ x = 14
∴ \(\frac{2}{9}=\frac{14}{63}\)

Question 7.
Find the equivalent fraction of \(\frac{3}{5}\) having
(i) denominator 30
(ii) numerator 27.
Solution:
(i) \(\frac{3}{5}\) having denominator 30
Multiply and divide the fraction by 6, we get
\(\frac{3}{5} \times \frac{6}{6}=\frac{18}{30}\)

(ii) \(\frac{3}{5}\) having numerator 27
Multiply and divide the fraction by 9, we get
\(\frac{3}{5} \times \frac{9}{9}=\frac{27}{45}\)

Question 8.
Replace ‘…..’ in each of the following by the correct number.

Solution:

Question 9.
Check whether the given pairs of fractions are equivalent:

Solution:

Question 10.
Reduce the following fractions to simplest form:

Solution:

Question 11.
Convert the following fractions into equivalent like fractions:

Solution:

ML Aggarwal Class 6 Solutions for ICSE Maths

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Objective Type Questions

Mental Maths
Question 1.
Fill in the blanks:
(i) The only natural number which has exactly one factor is ……….
(ii) The only prime number which is even is ……….
(iii) The HCF of two co-prime numbers is ……….
(iv) Two perfect numbers are ………. and ……….
(v) The only prime-triplet is ……….
Solution:
(i) The only natural number which has exactly one factor is 1.
(ii) The only prime number which is even is 2.
(iii) The HCF of two co-prime numbers is 1.
(iv) Two perfect numbers are 6 and 28.
(v) The only prime-triplet is 3, 5, 7.

Question 2.
State whether the following statements are true (T) or false (F):
(i) Every natural number has a finite number of factors.
(ii) Every natural number has an infinite number of its multiples.
(iii) There are infinitely many prime numbers.
(iv) If two numbers are separately divisible by a number, then their difference is also divisible by that number.
(v) LCM of two prime numbers equals their product.
(vi) LCM of two co-prime numbers equals their product.
Solution:
(i) Every natural number has a finite number of factors. True
(ii) Every natural number has an infinite number of its multiples. True
(iii) There are infinitely many prime numbers. True
(iv) If two numbers are separately divisible by a number, then their difference is also divisible by that number. True
(v) LCM of two prime numbers equals their product. True
(vi) LCM of two co-prime numbers equals their product. True

Question 3.
State whether the following statements are true or false. If a statement is false, justify your answer.
(i) The sum of two prime numbers is always an even number.
(ii) The sum of two prime numbers is always a prime number.
(iii) The sum of two prime numbers can never be a prime number
(iv) No odd number can be written as the sum of two prime numbers.
(v) If two numbers are co-prime, then atleast one of them must be prime.
(vi) If a number is divisible by 18, it must be divisible by 3 and 6 both.
(vii) If a number is divisible by 2 and 4 both, it must be divisible by 8.
(viii) If a number is divisible by 3 and 6 both, it must be divisible by 18.
(ix) HCF of an even number and an odd number is always 1.
Solution:
(i) The sum of two prime numbers is always an even number. False
Correct:
2 and 7 both are prime numbers but their sum = 2 + 7 = 9, which is an odd number.

(ii) The sum of two prime numbers is always a prime number. False
Correct:
3 and 5 both are prime numbers but their sum = 3 + 5 = 8, which is a composite number.

(iii) The sum of two prime numbers can never
be a prime number. False
Correct:
2 and 5 both are prime numbers but their sum = 2 + 5 = 7, which is a prime number.

(iv) No odd number can be written as the sum of two prime numbers. False
Correct:
13 is an odd number and 13 = 2+11, which is the sum of two prime numbers.

(v) If two numbers are co-prime, then atleast one of them must be prime. False
Correct :
8 and 15 are co-prime numbers but neither 8 is prime nor 15 is prime.

(vi) If a number is divisible by 18, it must be divisible by 3 and 6 both. True

(vii) If a number is divisible by 2 and 4 both, it
must be divisible by 8. False
Correct :
20 is divisible by 2 and 4 both but 20 is not divisible by 8.

(viii)If a number is divisible by 3 and 6 both, it must be divisible by 18. False
Correct:
12 is divisible by 3 and 6 both bu 12 is not divisible by 18.

(ix) HCF of an even number and an odd number is always 1. False
Correct:
6 is even and 9 is odd but HCF of 6 and 9 is 3.

Multiple Choice Questions
Choose the correct answer from the given four options (4 to 28):
Question 4.
All factors of 6 are
(a) 1, 6
(b) 2, 3
(c) 1, 2, 3
(d) 1, 2, 3, 6
Solution:
The factors of 6 are 1, 2, 3, 6 (d)

Question 5.
Which of the following is an odd composite number?
(a) 7
(b) 9
(c) 11
(d) 12
Solution:
9, is an odd composite number. (c)

Question 6.
The number of even numbers between 68 and 90 is
(a) 10
(b) 11
(c) 12
(d) 31
Solution:
The even numbers between 68 and 90 is 70, 72, 74, 76, 78, 80, 82, 84, 86, 88 = 10 numbers (a)

Question 7.
Which of the following is a prime number?
(a) 69
(b) 87
(c) 91
(d) 97
Solution:
Since, the factors of 97 are 1 and 97
97 is a prime number. (d)

Question 8.
Which of the following is a pair of twin- prime number?
(a) 19, 21
(b) 43, 47
(c) 59, 61
(d) 73, 79
Solution:
59, 61
Pairs of prime numbers whose difference is 2 are called twin-prime numbers. (c)

Question 9.
The number of distinct prime factors of the largest 4-digit number is
(a) 2
(b) 3
(c) 5
(d) none of these
Solution:
Largest 4 digit number = 9999

3 is prime factor. (b)

Question 10.
The number of distinct prime factors of the smallest 5-digit number is
(a) 2
(b) 4
(c) 6
(d) 8
Solution:
Smallest 5-digit number = 10000

Number of distinct prime factors of smallest 5-digit number = 2 (a)

Question 11.
The sum of the prime factors of 1729 is
(a) 13
(b) 19
(c) 32
(d) 39
Solution:

Prime factors of 1729 are 7, 13 and 19 Sum of prime factors = 7 + 13 + 19 = 39 (d)

Question 12.
Which of the following is a pair of co-prime numbers?
(a) 8, 45
(b) 3, 18
(c) 5, 35
(d) 6, 39
Solution:
8, 15
The factors of 8 are 1, 2, 4, 8 The factors of 15 are 1, 3, 5, 15 The common factors of 8 and 15 is 1 They are co-prime. (a)

Question 13.
Every natural number has an infinite number of
(a) prime factors
(b) factors
(c) multiples
(d) none of these
Solution:
Multiples
e.g. Multiples of 2 = 2, 4, 6, 8, 10, 12, 14, 16, …….. (c)

Question 14.
Which of the following numbers is divisible by 4?
(a) 308594
(b) 506784
(c) 732106
(d) 9301538
Solution:
506784
Because the number formed by tens and ones digits is divisible by 4 i.e. 84 ÷ 4 = 21 (b)

Question 15.
Which of the following numbers is divisible by 8?
(a) 503786
(b) 505268
(c) 305678
(d) 703568
Solution:
703568
Because the number formed by hundred, tens
and ones digit is divisible by 8
i. e. 568 – 8 = 71 (d)

Question 16.
Which of the following numbers is divisible by 3?
(a) 50762
(b) 42063
(c) 52871
(d) 37036
Solution:
42063
Because sum of its digits is = 4 + 2 + 0 + 6 + 3 = 15 Which is divisible by 3 (b)

Question 17.
Which of the following numbers is divisible by 9?
(a) 972063
(b) 730542
(c) 785423
(d) 5612844
Solution:
972063
Because sum of digits
= 9 + 7 + 2 + 0 + 6 + 3 = 27 Which is divisible by 9 (a)

Question 18.
Which of the following numbers is divisible by 6?
(a) 560324
(b) 650374
(c) 798653
(d) 750972
Solution:
750972
Because sum of its digit
= 7 + 5 + 0 + 9 + 7 + 2 = 30 Which is divisible by 3.
Hence it is divisible by 6. (d)

Question 19.
The digit by which ‘*’ should be replaced in 54 * 281 so that the number formed is divisible by 9 is
(a) 6
(b) 7
(c) 8
(d) 9
Solution:
For a number to be divisible by 9, sum of its digits should be divisible by 9.
Sum of given digits in 54 * 281
= 5 + 4 + 2 + 8 + 1 = 20.
If we add 7, it becomes 27, which is divisible by 9.
∴ * is to be replaced by 7. (b)

Question 20.
The digit by which should be replaced in 7254 * 98 so that the number formed is divisible by 22 is
(a) 0
(b) 1
(c) 2
(d) 6
Solution:
For a number to be divisible by 22, sum of its digits should be divisible by 2 and by 11.
Since, the last digit of 7254 * 98 is 8, which is divisible by 2.
Now,
Sum of the digits at odd places = 7 + 5 + 8 = 20
Sum of the digits at even places = 9 + 4 + 2 = 15
∴ Their Difference = 20 – 15 = 5
Since, 5 is not divisble by 11, so to make a number divisible by 11 we must add 6.
∴ * is to be replaced by 6 (d)

Question 21.
If a number is divisible by 5 and 6 both, then it may not be divisible by
(a) 10
(b) 15
(c) 30
(d) 60
Solution:
60 (d)

Question 22.
The number of common prime factors of 60, 75 and 105 is
(a) 2
(b) 3
(c) 4
(d) 5
Solution:
60, 75 and 105

=2 × 2 × 3 × 5 × 5 × 7 = 2 (a)

Question 23.
The H.C.F. of 144 and 198 is
(a) 6
(b) 9
(c) 12
(d) 18
Solution:
H.C.F. of 144 = 2 × 2 × 2 × 2 × 3 × 3
H.C.F. of 198 = 2 × 3 × 3 × 11

∴ H. C. F of 144 and 198
= 2 × 3 × 3 = 18 (d)

Question 24.
The L.C.M. of 30 and 45 is
(a) 15
(b) 30
(c) 45
(d) 90
Solution:
L.C.M. of 30 and 45 is 90

∴ L.C.M. = 3 × 5 × 2 × 3 = 90 (d)

Question 25.
The L.C.M. of 4 and 44 is
(a) 4
(b) 11
(c) 44
(d) 176
Solution:
LCM of 4 and 44 is 44

∴ L.C.M = 4 × 11 =44 (c)

Question 26.
The LCM of 7 and 13 is 1
(a) 1
(b) 7
(c) 13
(d) 91
Solution:
LCM of 7 and 13 is

LCM of 7 and 13 is 91
L.C.M. = 7 × 13 = 91 (d)

Question 27.
If H.C.F. of two numbers is 15 and their product is 1575, then their L.C.M. is
(a) 15
(b) 105
(c) 525
(d) 1575
Solution:
Product of numbers =1575
H.C.F. = 15
We know,
L.C. M = \(\frac{\text { Product of numbers }}{\text { H.C.F. }}\)
\(=\frac{1575}{15}=105\) (b)

Question 28.
If the LCM of two natural numbers is 180, then which of the following is not the HCF of the numbers?
(a) 45
(b) 60
(c) 75
(d) 90
Solution:
L.C.M. of 2 natural numbers = 180
We know that,
L.C.M. of 2 numbers is always exactly divisible by their H.C.F.
∴ Taking (a) 45 as H.C.F.

Here remainder = 0
∴ 45 is H.C.F.
Now, taking (b) 60 as H.C.F.

Here remainder = 0
∴ 60 is also H.C.F.
Now, taking 75 as H.C.F.

Here, remainder = 30
i. e. remainder ≠ 0
Hence, 75 is not the H.C.F. of two natural numbers whose L.C.M. is 180
Hence, answer is (c).

Value Based Questions
Question 1.
To teach the value of gratitude and appreciation to the students, a school organised a ‘Card Making’ activity in which the students were asked to make “THANK YOU CARDS” for the people who helped them in some way. Assorted cards were made with different titles. Their numbers are given below:
T cards for teachers = 120
F cards for friends = 540
S cards for servants = 90
P cards for parents = 240 and
G cards for grandparents = 150
(i) Find the HCF and LCM of all the different number of cards.
(ii) Find HCF and LCM of maximum and minimum number of cards.
(iii) Is the number of T-cards is a factor of number of P-cards?
Solution:
(i) HCF of 120, 540, 90, 240, 150


∴ HCF = 30
Now, LCM of 120, 540, 90, 240 and 150 is

∴ LCM = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 5 × 5
= 10800

(ii) Maximum number of cards = 540
Minimum number of cards = 90
∴ HCF is as follow :

Hence, HCF of 90 and 540 is 90
LCM of 90 and 540 is as follow :

LCM = 2 × 2 × 3 × 3 × 3 × 5 = 540

(iii) Yes.
T cards = 120
P cards = 240
240 = 120 × 2

Higher Order Thinking Skills (Hots)
Question 1.
Write 2-digit odd numbers whose sum of digits is 8.
Solution:
17, 71, 35, 53

Question 2.
Write all pairs of 2-digit twin primes such that on changing the places of their digits, they still remain prime numbers.
Solution:
11, 13, 71, 73

Question 3.
There are just four natural numbers less than 100, which have exactly three factors. One of them is 25, what are the other three? What can be said about these numbers?
Solution:
Four natural numbers less than 100 which have three factors :
One of them is 25 = 1, 5, 25
Second is 49 = 1, 7, 49
Third is 9 = 1, 3, 9
Fourth is 4 = 1, 2, 4

ML Aggarwal Class 6 Solutions for ICSE Maths

ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Check Your Progress

Question 1.
Write all factors of:
(i) 88
(ii) 105
(iii) 96
Solution:
(i) 88 = {1, 2, 4, 8, 11, 22, 44, 88}
(ii) 105 = {1, 3, 5, 7, 15, 21, 35, 105}
(iii) 96 = {1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96}

Question 2.
Find the common mutliples of 8 and 12.
Solution:
The multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64 72, 80, 88, 96, 104,
The multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108,
The common multiples of 8 and 12 are 24, 48, 72, 96

Question 3.
Which of the following pairs of numbers are co-prime?
(i) 25 and 105
(ii) 59 and 97
(iii) 161 and 192
Solution:
(i) 25 and 105
The factors of 25 are 1, 5, 25
The factors of 105 are 1,3, 5, 7, 15, 21, 35, 105
The common factors of 25 and 105 are 1, 5
∴ They are not co-prime

(ii) 59 and 97
The factors of 59 are 1, 59
The factors of 97 are 1, 97
The common factors of 59 and 97 is 1
∴ They are co-prime

(iii) 161 and 192
The factors of 161 are 1, 161
The factors of 192 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 192
The common factors of 161, 192 is 1
∴ They are co-prime.

Question 4.
Using divisibility tests, determine which of the following numbers are divisible by 4, 6, 8, 9 or 11:
(i) 197244
(ii) 613440
(iii) 4100448
Solution:
197244: divisible by 4, 6, 9.
It is divisible by 4 as last two digits is divisible by 4.
It is divisible by 6 as last digit of given number is divisible 2 and their sum is also divisible by 3.
Sum of digits 1 + 9 + 7 + 2 + 4 + 4 = 27 Which is divisible by 3.
It is not divisible by 8 as the sum of last three digit 2 + 4 + 4 = 10, is not divisible by 8.
It is divisible by 9 as the sum of its digits 27 is divisible by 9.
It is not divisible by 11 as the difference of the sum of alternate number 1 + 7 + 4 = 12 and 9 + 2 + 4 = 15, (15 – 12) = 3 is not divisible by 11.
∴ 197244 is divisible by 4, 6 and 9.

(ii) 613440 : divisible by 4, 6, 8, 9.
It is divisible by 4 as last two digit is divisible by 4.
It is divisible by 6 as the sum of all digits (6 + 1 + 3 + 4 + 4 + 0)=18 is divisible by 3 and by 2 also as last digit is 0.
It is divisible by 8 as the sum of last three digits (4 + 4 + 0) = 8 is divisible 8.
It is also divisible by 9 as the sum of its digits 18 is divisible by 9.
It is not divisible by 11 as the difference of the sum of alternate number 6 + 3 + 4 = 13 and 1 + 4 + 0 = 5, (13 – 5) = 8 is not divisible by 11.
613440 is divisible by 4, 6, 8 and 9.

(iii) 4100448: divisible by 4, 6, 8, 11.
It is divisible by 4 as last two digit is divisible by 4.
It is divisible by 6 as the sum of all digits 4 + 1 + 0 + 0 + 4 + 4 + 8 = 21 is divisible by 3 and also last digit is divisible by 2.
It is divisible by 8 as the sum of last three digits 4 + 4 + 8 = 16 is divisible by 8.
It is not divisible by 9 as the sum of its digit 21 is not divisible by 9.
It is divisible by 11 as the difference of the sum of alternate number 4 + 0 + 4 + 8= 16 and 1 + 0 + 4 = 5, (16 – 6) = 11 which is divisible by 11.
∴ 4100448 is divisible by 4, 6, 8, 11.

Question 5.
In 92 * 389, replace * by a digit so that the number formed is divisible by 11.
Solution:
The given number is 92 * 389
Here, * occur at odd place.
Sum of digits at odd place = 9 + 8 = 17 (Except *)
Sum of digits at even place = 2 + 3 + 9 = 14
Their difference = 17 – 14 = 3
If ‘*’ is replaced by 8, then sum of digits at odd place = 9 + 8 + 8 = 25
Their difference (Sum of digits at odd places – Sum of digits at even places)
= 25 – 14 = 11
Which is divisible by 11
∴ ‘*’ is to be replaced by the digit 8.

Question 6.
Find the prime factorisation of the following numbers:
(i) 168
(ii) 2304
Solution:
(i) 168

= 2 × 2 × 2 × 3 × 7

(ii) 2304

= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3

Question 7.
Find the G.C.D. of the given numbers by prime factorisation method :
(i) 24,45
(ii) 180, 252, 324
Solution:
(i) 24, 45
24 = 2 × 2 × 2 × 3
45 = 3 × 3 × 5
The greatest common factor is 3.
G.C.D = 3

(ii) 180, 252, 324
180 = 2 × 2 × 3 × 3 × 5

252 = 2 × 2 × 3 × 3 × 7

324 = 2 × 2 × 3 × 3 × 3 × 3

G.C.D = 2 × 2 × 3 × 3 = 36
We notice that 2 and 3 both occurs as the common factor in the given numbers two time each.

Question 8.
Find the H.C.F of the given numbers by division method.
(i) 54, 82
(ii) 84, 120, 156
Solution:
(i) 54, 82
H.C.F = 2

(ii) 84, 120, 156
Solution:
H.C.F = 12

Question 9.
Find the L.C.M of the given numbers by prime factorisation method.
(i) 27, 90
(ii) 36, 48, 210
Solution:
(i) 27, 90
= 2 × 3 × 3 × 3 × 5 = 270

(ii) 36, 48, 210
= 2 × 2 × 3 × 3 × 2 × 2 × 5 × 7 = 5040

Question 10.
Find the L.C.M of the given numbers by division method:
(i) 48, 60
(ii) 112, 168, 266
Solution:
(i) 48, 60
= 2 × 2 × 3 × 4 ×5 = 240

(ii) 112, 168, 266
= 2 × 2 × 2 × 7 × 2 × 3 × 19 = 6384

Question 11.
Find the greatest number which divides 2706, 7041 and 8250 leaving remainder 6, 21 and 42 respectively.
Solution:
When 2706 is divided by the required number, 6 is left as a remainder. So, 2706 – 6 = 2700 i.e. 2700 is exactly divisible by that number.
Similarly, 7041 – 21 = 7020 is exactly divisible by that number.
Similarly, also, 8250 – 42 = 8208 is exactly divisible by that number.
Therefore, 2700, 7020 and 8208 are divisible by that number.
Thus, the required number is the H.C.F. of 2700, 7020 and 8208.
First, we find H.C.F. of 2700 and 7020.

∴ The H.C.F. of 2700, 7020 and 8208 is 108.
Hence the required number is 108

Question 12.
Find the least number which on decreasing by 20 is exactly divisible by 18, 21, 28 and 30.
Solution:
First, we find the least number which is exactly divisible by the numbers 18, 21, 28 and 30. For this, we find the L.C.M. of 18, 21, 28 and 30.

∴ L.C.M. = 2 × 2 × 3 × 3 × 5 × 7 = 1260
According to given, the required number will be 20 more than 1260.
The required number = 1260 + 20 = 1280

Question 13.
There are three heaps of rice weighing 120 kg, 144 kg and 204 kg. Find the maximum capacity of a bag so that the rice of each heap can be packed in exact number of bags.
Solution:
Weights of three heaps = 120 kg, 144 kg and 204 kg

∴ Maximum capacity of a bag, which exactly divides the heaps in exact number HCF of 120, 144, 204 = 12
∴  Required capacity of bag = 12 kg

Question 14.
Three bells are ringing continuously at intervals of 30, 36 and 45 minutes respectively. At what time will they ring together again if they ring simultaneously at 8 a.m.
Solution:
L.C.M = 2 × 3 × 3 × 2 × 5 = 180.
After 180 minute at 11: 00 a.m.

Question 15.
Two numbers are co-prime and their L.C.M. is 4940. If one of the numbers is 65, find the other number.
Solution:
One number = 65
and let the other number = x
We know that,
Two numbers are co-prime if their HCF is 1
Now, H.C.F. × L.C.M. of two numbers = Product of given two numbers
1 × 4940 = 65 × x
⇒ 4940 = 65 × x
⇒ 65 × x = 4940
⇒ x = 4940 ÷ 65 = 76

∴ The other number is 76

ML Aggarwal Class 6 Solutions for ICSE Maths