ML Aggarwal Class 6 Solutions for ICSE Maths Chapter 4 Playing with Numbers Check Your Progress
Question 1.
Write all factors of:
(i) 88
(ii) 105
(iii) 96
Solution:
(i) 88 = {1, 2, 4, 8, 11, 22, 44, 88}
(ii) 105 = {1, 3, 5, 7, 15, 21, 35, 105}
(iii) 96 = {1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96}
Question 2.
Find the common mutliples of 8 and 12.
Solution:
The multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64 72, 80, 88, 96, 104,
The multiples of 12 are 12, 24, 36, 48, 60, 72, 84, 96, 108,
The common multiples of 8 and 12 are 24, 48, 72, 96
Question 3.
Which of the following pairs of numbers are co-prime?
(i) 25 and 105
(ii) 59 and 97
(iii) 161 and 192
Solution:
(i) 25 and 105
The factors of 25 are 1, 5, 25
The factors of 105 are 1,3, 5, 7, 15, 21, 35, 105
The common factors of 25 and 105 are 1, 5
∴ They are not co-prime
(ii) 59 and 97
The factors of 59 are 1, 59
The factors of 97 are 1, 97
The common factors of 59 and 97 is 1
∴ They are co-prime
(iii) 161 and 192
The factors of 161 are 1, 161
The factors of 192 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 192
The common factors of 161, 192 is 1
∴ They are co-prime.
Question 4.
Using divisibility tests, determine which of the following numbers are divisible by 4, 6, 8, 9 or 11:
(i) 197244
(ii) 613440
(iii) 4100448
Solution:
197244: divisible by 4, 6, 9.
It is divisible by 4 as last two digits is divisible by 4.
It is divisible by 6 as last digit of given number is divisible 2 and their sum is also divisible by 3.
Sum of digits 1 + 9 + 7 + 2 + 4 + 4 = 27 Which is divisible by 3.
It is not divisible by 8 as the sum of last three digit 2 + 4 + 4 = 10, is not divisible by 8.
It is divisible by 9 as the sum of its digits 27 is divisible by 9.
It is not divisible by 11 as the difference of the sum of alternate number 1 + 7 + 4 = 12 and 9 + 2 + 4 = 15, (15 – 12) = 3 is not divisible by 11.
∴ 197244 is divisible by 4, 6 and 9.
(ii) 613440 : divisible by 4, 6, 8, 9.
It is divisible by 4 as last two digit is divisible by 4.
It is divisible by 6 as the sum of all digits (6 + 1 + 3 + 4 + 4 + 0)=18 is divisible by 3 and by 2 also as last digit is 0.
It is divisible by 8 as the sum of last three digits (4 + 4 + 0) = 8 is divisible 8.
It is also divisible by 9 as the sum of its digits 18 is divisible by 9.
It is not divisible by 11 as the difference of the sum of alternate number 6 + 3 + 4 = 13 and 1 + 4 + 0 = 5, (13 – 5) = 8 is not divisible by 11.
613440 is divisible by 4, 6, 8 and 9.
(iii) 4100448: divisible by 4, 6, 8, 11.
It is divisible by 4 as last two digit is divisible by 4.
It is divisible by 6 as the sum of all digits 4 + 1 + 0 + 0 + 4 + 4 + 8 = 21 is divisible by 3 and also last digit is divisible by 2.
It is divisible by 8 as the sum of last three digits 4 + 4 + 8 = 16 is divisible by 8.
It is not divisible by 9 as the sum of its digit 21 is not divisible by 9.
It is divisible by 11 as the difference of the sum of alternate number 4 + 0 + 4 + 8= 16 and 1 + 0 + 4 = 5, (16 – 6) = 11 which is divisible by 11.
∴ 4100448 is divisible by 4, 6, 8, 11.
Question 5.
In 92 * 389, replace * by a digit so that the number formed is divisible by 11.
Solution:
The given number is 92 * 389
Here, * occur at odd place.
Sum of digits at odd place = 9 + 8 = 17 (Except *)
Sum of digits at even place = 2 + 3 + 9 = 14
Their difference = 17 – 14 = 3
If ‘*’ is replaced by 8, then sum of digits at odd place = 9 + 8 + 8 = 25
Their difference (Sum of digits at odd places – Sum of digits at even places)
= 25 – 14 = 11
Which is divisible by 11
∴ ‘*’ is to be replaced by the digit 8.
Question 6.
Find the prime factorisation of the following numbers:
(i) 168
(ii) 2304
Solution:
(i) 168

= 2 × 2 × 2 × 3 × 7
(ii) 2304

= 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3
Question 7.
Find the G.C.D. of the given numbers by prime factorisation method :
(i) 24,45
(ii) 180, 252, 324
Solution:
(i) 24, 45
24 = 2 × 2 × 2 × 3
45 = 3 × 3 × 5
The greatest common factor is 3.
G.C.D = 3
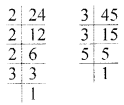
(ii) 180, 252, 324
180 = 2 × 2 × 3 × 3 × 5

252 = 2 × 2 × 3 × 3 × 7
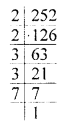
324 = 2 × 2 × 3 × 3 × 3 × 3

G.C.D = 2 × 2 × 3 × 3 = 36
We notice that 2 and 3 both occurs as the common factor in the given numbers two time each.
Question 8.
Find the H.C.F of the given numbers by division method.
(i) 54, 82
(ii) 84, 120, 156
Solution:
(i) 54, 82
H.C.F = 2
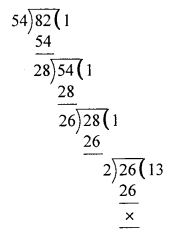
(ii) 84, 120, 156
Solution:
H.C.F = 12
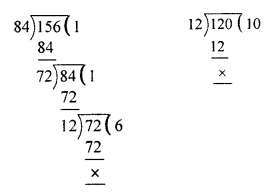
Question 9.
Find the L.C.M of the given numbers by prime factorisation method.
(i) 27, 90
(ii) 36, 48, 210
Solution:
(i) 27, 90
= 2 × 3 × 3 × 3 × 5 = 270

(ii) 36, 48, 210
= 2 × 2 × 3 × 3 × 2 × 2 × 5 × 7 = 5040
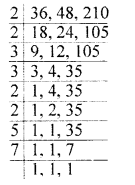
Question 10.
Find the L.C.M of the given numbers by division method:
(i) 48, 60
(ii) 112, 168, 266
Solution:
(i) 48, 60
= 2 × 2 × 3 × 4 ×5 = 240

(ii) 112, 168, 266
= 2 × 2 × 2 × 7 × 2 × 3 × 19 = 6384

Question 11.
Find the greatest number which divides 2706, 7041 and 8250 leaving remainder 6, 21 and 42 respectively.
Solution:
When 2706 is divided by the required number, 6 is left as a remainder. So, 2706 – 6 = 2700 i.e. 2700 is exactly divisible by that number.
Similarly, 7041 – 21 = 7020 is exactly divisible by that number.
Similarly, also, 8250 – 42 = 8208 is exactly divisible by that number.
Therefore, 2700, 7020 and 8208 are divisible by that number.
Thus, the required number is the H.C.F. of 2700, 7020 and 8208.
First, we find H.C.F. of 2700 and 7020.

∴ The H.C.F. of 2700, 7020 and 8208 is 108.
Hence the required number is 108
Question 12.
Find the least number which on decreasing by 20 is exactly divisible by 18, 21, 28 and 30.
Solution:
First, we find the least number which is exactly divisible by the numbers 18, 21, 28 and 30. For this, we find the L.C.M. of 18, 21, 28 and 30.
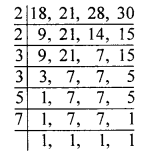
∴ L.C.M. = 2 × 2 × 3 × 3 × 5 × 7 = 1260
According to given, the required number will be 20 more than 1260.
The required number = 1260 + 20 = 1280
Question 13.
There are three heaps of rice weighing 120 kg, 144 kg and 204 kg. Find the maximum capacity of a bag so that the rice of each heap can be packed in exact number of bags.
Solution:
Weights of three heaps = 120 kg, 144 kg and 204 kg
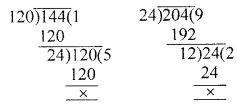
∴ Maximum capacity of a bag, which exactly divides the heaps in exact number HCF of 120, 144, 204 = 12
∴ Required capacity of bag = 12 kg
Question 14.
Three bells are ringing continuously at intervals of 30, 36 and 45 minutes respectively. At what time will they ring together again if they ring simultaneously at 8 a.m.
Solution:
L.C.M = 2 × 3 × 3 × 2 × 5 = 180.
After 180 minute at 11: 00 a.m.

Question 15.
Two numbers are co-prime and their L.C.M. is 4940. If one of the numbers is 65, find the other number.
Solution:
One number = 65
and let the other number = x
We know that,
Two numbers are co-prime if their HCF is 1
Now, H.C.F. × L.C.M. of two numbers = Product of given two numbers
1 × 4940 = 65 × x
⇒ 4940 = 65 × x
⇒ 65 × x = 4940
⇒ x = 4940 ÷ 65 = 76

∴ The other number is 76