Area Under a Curve

Area Under a Curve

Area of bounded regions

1. The area bounded by a cartesian curve y = f(x), x-axis and ordinates x = a and x = b is given by
   
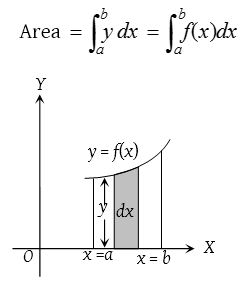
2. If the curve y = f(x) lies below x-axis, then the area bounded by the curve y = f(x) the x-axis and the ordinates x = a and x = b is negative. So, area is given by \(\left| \int _{ a }^{ b }{ ydx }  \right|\).
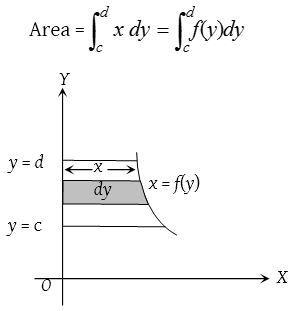
3. The area bounded by a cartesian curve x =f(y), y-axis and abscissae y = c and y = d is given by,
   
4. If the equation of a curve is in parametric form, let x = f(t), y = g(t) then
   ,
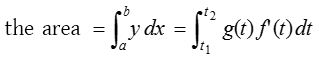   where t₁ and t₂ are the values of t respectively corresponding to the values of a and b of x.

Symmetrical area

If the curve is symmetrical about a co-ordinate axis (or a line or origin), then we find the area of one symmetrical portion and multiply it by the number of symmetrical portions to get the required area.

Area between two curves

1. When both curves intersect at two points and their common area lies between these points:
   If the curves  y₁ = f₁(x) and y₂ = f₂(x), where f₁(x) > f₂(x) intersect in two points A(x = a) and B(x = b), then common area between the curves is
   
   
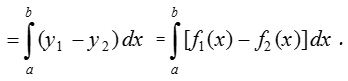
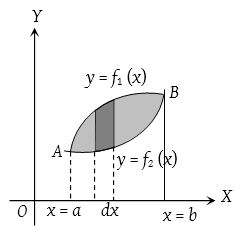
2. When two curves intersect at a point and the area between them is bounded by x-axis:
   Area bounded by the curves is
   
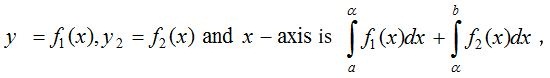
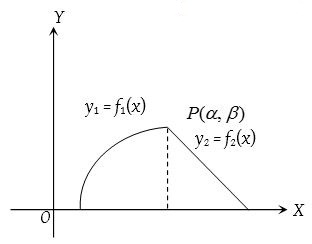   where P(α, β) is the point of intersection of the two curves.
3. Positive and negative area:
   Area is always taken as positive. If some part of the area lies above the x-axis and some part lies below x-axis, then the area of two parts should be calculated separately and then add their numerical values to get the desired area.

Volumes and surfaces of solids of revolution

If a plane curve is revolved about some axis in the plane of the curve, then the body so generated is known as solid of revolution. The surface generated by the perimeter of the curve is known as surface of revolution and the volume generated by the area is called volume of revolution.
For example, a right angled triangle when revolved about one of its sides (forming the right angle) generates a right circular cones.

(1) Volumes of solids of revolution

1. The volume of the solid generated by the revolution, about the x-axis, of the area bounded by the curve y = f(x), the ordinates at x = a, x = b and the x-axis is equal to \(\pi \int _{ a }^{ b }{ { y }^{ 2 }dx }\).
   
2. The revolution of the area lying between the curve x = f(y) the y-axis and the lines y = a and y = b is given by (interchanging x and y in the above formulae) \(\int _{ a }^{ b }{ { \pi x }^{ 2 }dy }\).
3. If the equation of the generating curve be given by x = f₁(t) and y = f₂(t) and it is revolved about x-axis, then the formula corresponding to \(\int _{ a }^{ b }{ { \pi y }^{ 2 }dx }\) becomes 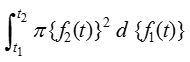where f₁ and f₂ are the values of t corresponding to x = a  and  x = b.

(2) Area of surfaces of revolution

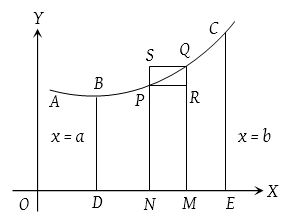
1. The curved surface of the solid generated by the revolution, about the x- axis, of the area bounded by the curve y = f(x), the ordinates at x = a, x = b and the x-axis is equal to \(2\pi \int _{ x=a }^{ x=b }{ { y }ds }\).
   
2. If the arc of the curve y = f(x) revolves about y-axis, then the area of the surface of revolution (between proper limits)
   
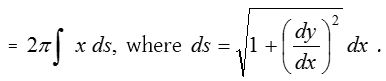
3. If the equation of the curve is given in the parametric form x = f₁(t) and y = f₂(t), and the curve revolves about x-axis, then we get the area of the surface of revolution
   
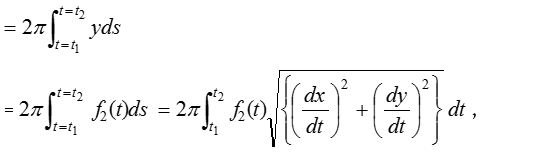
   where t₁ and t₂ are the values of the parameter corresponding to x = a and x = b.

(3) Volume and surface of the frustum of a cone
If r₁, r₂ be the radii of the circular ends and k is the distance between centres of circular ends and l be the slant height, then

1. Volume of frustum of cone = πk/3(r₁² + r₁r₂ + r₂²)
2. Curved surface area of frustum of cone = π(r₁ + r₂)l
3. Whole surface area of frustum of cone = π(r₁ + r₂)l + πr₁² + πr₂².

(4) Volume and surface of the frustum of a sphere

Let the thickness of the frustum of sphere is k and radii of the circular ends of the frustum are r₁ and r₂, then

1. Volume of the frustum of sphere = πk/6(3r₁² + 3r₂² + k²)
2. Curved surface area of frustum of sphere = 2πak (where a is radius of circle)
3. Whole surface area of frustum of sphere = (2πak + πr₁² + πr₂²).

Area Under a Curve Problems with Solutions

1.

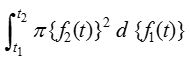
Solution:

2.

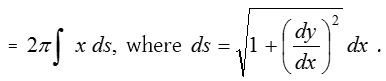
Solution:

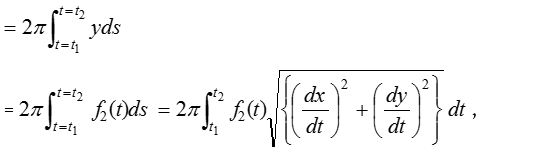
3.

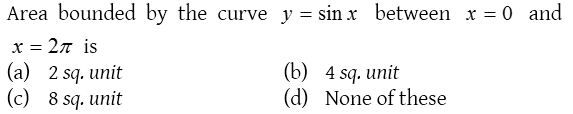
Solution:

4.

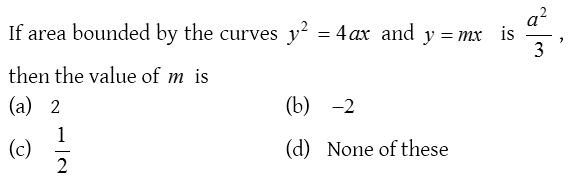
Solution:

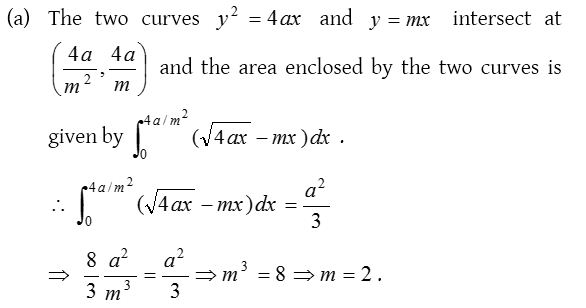
5.

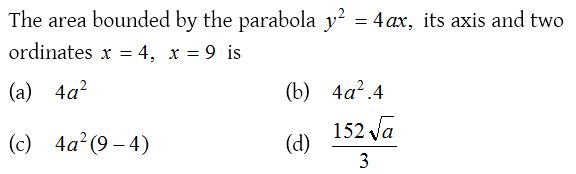
Solution:

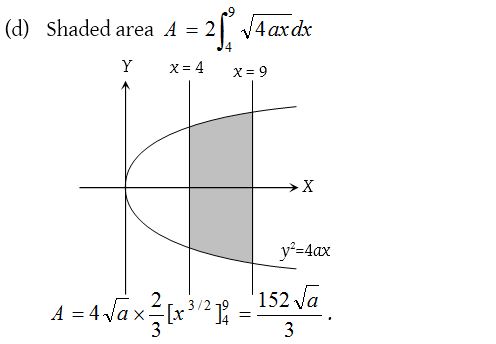
6.

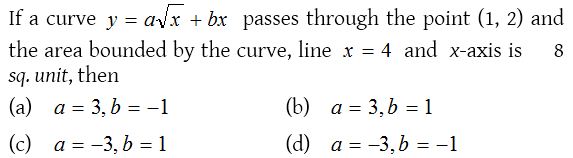
Solution:

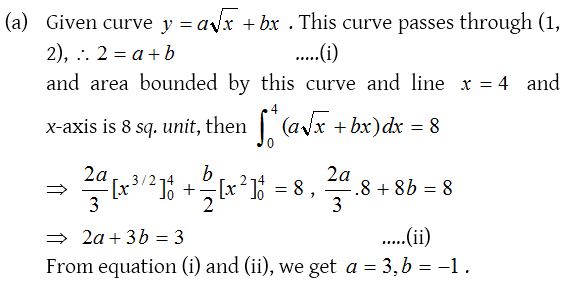
7.

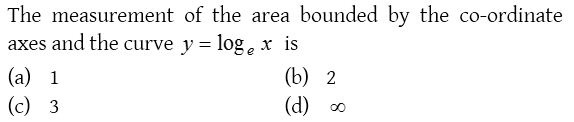
Solution:

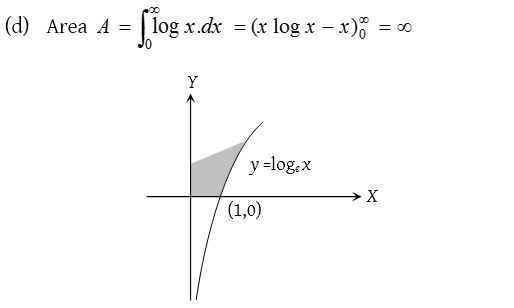
8.

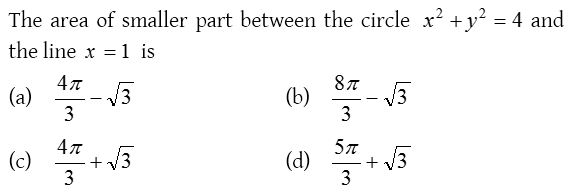
Solution:

9.

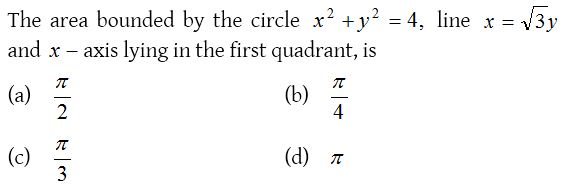
Solution:

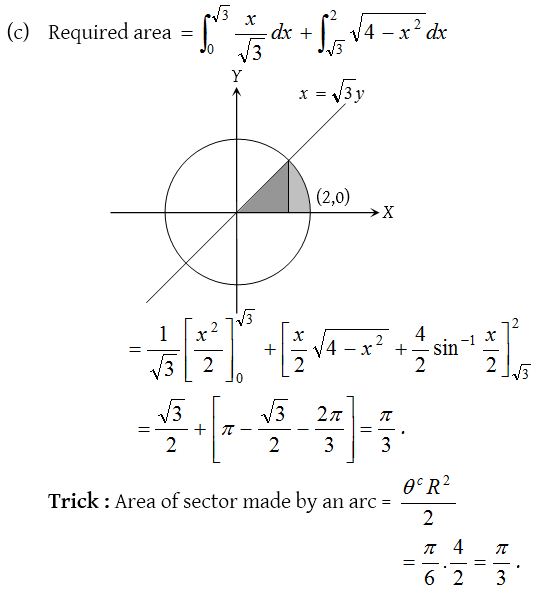
10.

Solution:

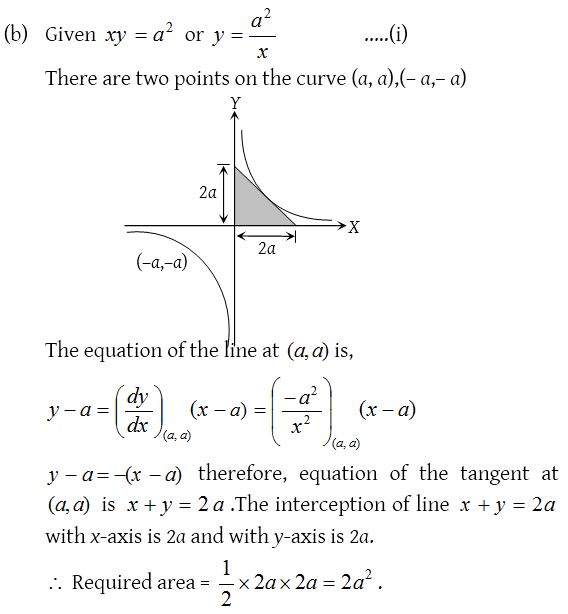
11.

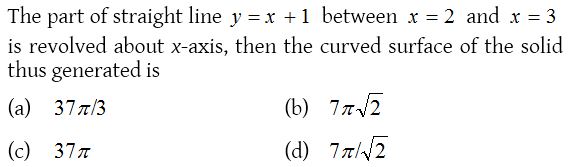
Solution:

12.

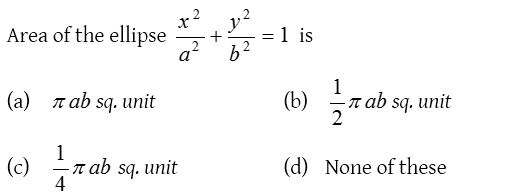
Solution: