Trigonometric Ratios Of Some Specific Angles
The angles 0°, 30°, 45°, 60°, 90° are angles for which we have values of T.R.
θ | 0° | 30° | 45° | 60° | 90° |
Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 |
Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 |
Tan | 0 | 1/√3 | 1 | √3 | ∞ |
| Cosec | ∞ | 2 | √2 | 2/√3 | 1 |
| Sec | 1 | 2/√3 | √2 | 2 | ∞ |
| Cot | ∞ | √3 | 1 | 1/√3 | 0 |
Trigonometric Ratios Of Some Specific Angles With Examples

Example 1: Evaluate each of the following in the simplest form:
(i) sin 60º cos 30º + cos 60º sin 30º
(ii) sin 60º cos 45º + cos 60º sin 45º
Sol. (i) sin 60º cos 30º + cos 60º sin 30º
\(=\frac{\sqrt{3}}{2}\times \frac{\sqrt{3}}{2}+\frac{1}{2}\times \frac{1}{2}=\frac{3}{4}+\frac{1}{4}=1\)
(ii) sin 60º cos 45º + cos 60º sin 45º
\( =\frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{2}}+\frac{1}{2}\times \frac{1}{\sqrt{2}} \)
\( =\frac{\sqrt{3}}{2\sqrt{2}}+\frac{1}{2\sqrt{2}}=\frac{\sqrt{3}+1}{2\sqrt{2}} \)
Example 2: Evaluate the following expression:
(i) tan 60º cosec2 45º + sec2 60º tan 45º
(ii) 4cot2 45º – sec2 60º + sin2 60º + cos2 90º.
Sol. (i) tan 60º cosec2 45º + sec2 60º tan 45º
= tan 60º (cosec 45º)2 + (sec 60º)2 tan 45º
= √3 × (√2)2 + (2)2 × 1
= √3 × 2 + 4 = 4 + 2 √3
(ii) 4cot2 45º – sec2 60º + sin2 60º + cos2 90º
= 4(cot 45º)2 – (sec 60º)2 + (sin 60º)2 + (cos 90º)2
= 4 × (1)2 – (2)2 + (√3/2)2 + 0
= 4 – 4 + 3/4 + 0 = 3/4
Example 3: Show that:
(i) 2(cos245º + tan260º) – 6(sin245º – tan230º) = 6
(ii) 2(cos460º + sin430º) – (tan260º + cot245º) + 3 sec230º = 1/4
Sol. (i) 2(cos245º + tan260º) – 6(sin245º – tan230º)
\( =2\left( {{\left( \frac{1}{\sqrt{2}} \right)}^{2}}+{{(\sqrt{3})}^{2}} \right)-6\left( {{\left( \frac{1}{\sqrt{2}} \right)}^{2}}-{{\left( \frac{1}{\sqrt{3}} \right)}^{2}} \right) \)
\( =2\left( \frac{1}{2}+3 \right)-6\left( \frac{1}{2}-\frac{1}{3} \right)=2\left( \frac{1+6}{2} \right)-6\left( \frac{3-2}{6} \right) \)
\( =2\times \frac{7}{2}-6\times \frac{1}{6}=7-1=6 \)
(ii) 2(cos460º + sin430º) – (tan260º + cot245º) + 3 sec230º
\( =2\left( {{\left( \frac{1}{2} \right)}^{4}}+{{\left( \frac{1}{2} \right)}^{4}} \right)-\left( {{(\sqrt{3})}^{2}}+{{(1)}^{2}} \right)+3{{\left( \frac{2}{\sqrt{3}} \right)}^{2}} \)
\( =2\left( \frac{1}{16}+\frac{1}{16} \right)\left( 3+1 \right)+3\times \frac{4}{3} \)
\( =2\times ~\frac{1}{8}-4+4=\frac{1}{4} \)
Example 4: Find the value of x in each of the following :
(i) tan 3x = sin 45º cos 45º + sin 30º
(ii) cos x = cos 60º cos 30º + sin 60º sin 30º
Sol. (i) tan 3x = sin 45º cos 45º + sin 30º
\( \Rightarrow tan\text{ }3x=\frac{1}{\sqrt{2}}\times \frac{1}{\sqrt{2}}+\frac{1}{2} \)
\( \Rightarrow tan\text{ }3x=\frac{1}{2}+\frac{1}{2} \)
⇒ tan 3x = 1
⇒ tan 3x = tan 45º
⇒ 3x = 45º ⇒ x = 15º
(ii) cos x = cos 60º cos 30º + sin 60º sin 30º
\( \Rightarrow cos\text{ }x=\frac{1}{2}\times \frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\times \frac{1}{2} \)
\( \Rightarrow cos\text{ }x=\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4} \)
⇒ cos x = √3/2
⇒ cos x = cos 30º
⇒ x = 30º
Example 5: If x = 30°, verify that
\((i)\tan 2x=\frac{2\tan x}{1-{{\tan }^{2}}x}\text{ }(ii)\sin x=\sqrt{\frac{1-\cos 2x}{2}}\)
Sol.(i) When x = 30°, we have 2x = 60° .
∴ tan 2x = tan 60° = √3
\( \text{And, }\frac{2\tan x}{1-{{\tan }^{2}}x}=\frac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ } \)
\( =\frac{2\times \frac{1}{\sqrt{3}}}{1-{{\left( \frac{1}{\sqrt{3}} \right)}^{2}}} \)
\( =\frac{2/\sqrt{3}}{1-\frac{1}{3}}=\frac{2/\sqrt{3}}{2/3}=\frac{2}{\sqrt{3}}\times \frac{3}{2}=\sqrt{3} \)
\( \tan 2x=\frac{2\tan x}{1-{{\tan }^{2}}x} \)
(ii) When x = 30°, we have 2x = 60°.
\( \sqrt{\frac{1-\cos 2x}{2}}=\sqrt{\frac{1-\cos 60{}^\circ }{2}} \)
\( \sqrt{\frac{1-\frac{1}{2}}{2}}=\sqrt{\frac{1}{4}}=\frac{1}{2} \)
And, sinx = sin30° = 1/2
\( \sin x=\frac{\sqrt{1-\cos 2x}}{2} \)
Example 6: Find the value of θ in each of the following :
(i) 2 sin 2θ = √3 (ii) 2 cos 3θ = 1
(i) 2 sin 2θ= √3
⇒ sin 2θ= √3/2
⇒ sin 2θ= sin 60°
⇒ 2θ= 60° ⇒ θ = 30°
(ii) 2 cos 3θ = 1
⇒ cos 3θ = 1/2
⇒ cos 3θ = cos 60°
⇒ 3θ = 60° ⇒ θ = 20°.
Example 7: If θ is an acute angle and sin θ = cos θ, find the value of 2 tan2θ + sin2θ – 1.
Sol. sin θ = cos θ
\( \Rightarrow \frac{\sin \theta }{\cos \theta }=\frac{\cos \theta }{\cos \theta } \)
[Dividing both sides by cos θ]
⇒ tanθ = 1
⇒ tanθ = tan45° ⇒ θ= 45°
∴ 2 tan2θ + sin2θ – 1
= 2tan245° + sin245° – 1
\( =2{{(2)}^{2}}+{{\left( \frac{1}{\sqrt{2}} \right)}^{2}}-1 \)
\( =2+\frac{1}{2}-1=\frac{5}{2}-1=\frac{3}{2} \)
Example 8: An equilateral triangle is inscribed in a circle of radius 6 cm. Find its side.
Sol. Let ABC be an equilateral triangle inscribed in a circle of radius 6 cm. Let O be the centre of the circle.
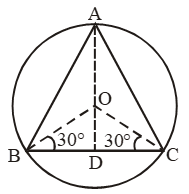
Then, OA = OB = OC = 6 cm.
Let OD be perpendicular from O on side BC. Then, D is mid-point of BC and OB and OC are bisectors of ∠B and ∠C respectively.
∴ ∠OBD = 30°
In ∆OBD, right angled at D, we have
∠OBD = 30° and OB = 6 cm.
\( \cos \angle OBD=\frac{BD}{OB}\Rightarrow \cos {{60}^{0}}=\frac{BD}{6} \)
\( \Rightarrow BD=6\cos {{60}^{0}}=6\times \frac{\sqrt{3}}{2}=3\sqrt{3}\text{ } \)
⇒ BC = 2 BD = 2(3√3 )cm = 6 √3 cm.
Example 9: Using the formula, sin(A – B) = sinA cosB – cosA sinB, find the value of sin 15º.
Sol. Let A = 45º and B = 30º. Then A – B = 15º. Putting A = 45º and B = 30º in the given formula, we get
sin(45º – 30º) = sin45º cos30º – cos45º sin30º
\( or,\sin (45{}^\text{o}-30{}^\text{o})=\frac{1}{\sqrt{2}}\times \frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}\times \frac{1}{2} \)
\( =\frac{\sqrt{3}-1}{2\sqrt{2}}\Rightarrow \sin 15{}^\text{o}=\frac{\sqrt{3}-1}{2\sqrt{2}} \)
Example 10: If tan (A + B) = √3 and tan (A – B) = 1/√3 ; 0° < A + B ≤ 90° ; A > B, find A and B.
tan (A + B) = √3 = tan 60° & tan (A – B) = 1/√3 = tan 30°
A + B = 60° …….(1)
A – B = 30° …….(2)
2A = 90° ⇒ A = 45°
adding (1) & (2)
A + B = 60
A – B = 30
Subtract equation (2) from (1)
A + B = 60
A – B = 30
2B = 30°
⇒ B = 15°. Ans.
Note: sin(A + B) = sin A cos B + cos A sin B
sin(A + B) ≠ sin A + sin B.