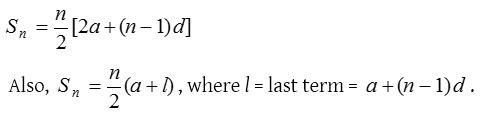Sum Of The First n Terms Of An Arithmetic Progression


The sum of first n terms of an A.P. is given by
Sn = n/2 [2a + (n – 1) d] or Sn = n/2 [a + Tn]
Note:
(i) If sum of n terms Sn is given then general term Tn = Sn – Sn-1 where Sn-1 is sum of (n – 1) terms of A.P.
(ii) nth term of an AP is linear in ‘n’
Example: an = 2 – n, an = 5n + 2 ……..
Also we can find common difference ‘d’ from an or Tn : d = coefficient of n
For an = 2 – n
∴ d = –1
Verification: by putting n = 1, 2, 3, 4,………
we get AP: 1, 0, –1, –2,……..
∴ d = 0 – 1 = –1
& for an = 5n + 2
d = 5
(iii) Sum of n terms of an AP is always quadratic in ‘n’
Example: Sn = 2n2 + 3n.
Example: Sn = n/4 (n + 1)
we can find ‘d’ also from Sn.
d = 2 (coefficient of n2)
for eg. : 2n2 + 3n, d = 2(2) = 4
Verification: Sn = 2n2 + 3n
at n = 1, S1 = 2 + 3 = 5 = first term
at n = 2, S2 = 2(2)2 + 3(2)
= 8 + 6 = 14 ≠ second term
= sum of first two terms.
∴ second term = S2 – S1 = 14 – 5 = 9
∴ d = a2 – a1 = 9 – 5 = 4
\( \text{Example: }{{S}_{n}}~=~\frac{n}{4}\left( n+1 \right) \)
\( {{S}_{n}}~=~\frac{{{n}^{2}}}{4}+\frac{n}{4} \)
\( \therefore d=2\left( \frac{1}{4} \right)=\frac{1}{2} \)
Sum Of The n Terms Of An Arithmetic Progression With Examples
Example 1: The sum of three numbers in A.P. is –3, and their product is 8. Find the numbers.
Solution. Let the numbers be (a – d), a, (a + d). Then,
Sum = – 3
⇒ (a – d) + a (a + d) = – 3
⇒ 3a = – 3
⇒ a = – 1
Product = 8
⇒ (a – d) (a) (a + d) = 8
⇒ a (a2 – d2) = 8
⇒ (–1) (1 – d2) = 8
⇒ d2 = 9 ⇒ d = ± 3
If d = 3, the numbers are –4, –1, 2. If d = – 3, the numbers are 2, – 1, –4.
Thus, the numbers are –4, –1, 2, or 2, – 1, – 4.
Example 2: Find four numbers in A.P. whose sum is 20 and the sum of whose squares is 120.
Solution. Let the numbers be (a – 3d), (a – d), (a + d), (a + 3d), Then
Sum = 20
⇒ (a – 3d) + (a – d) + (a + d) + (a + 3d) = 20
⇒ 4a = 20
⇒ a = 5
Sum of the squares = 120
(a – 3d)2 + (a – d)2 + (a + d)2 + (a + 3d)2 = 120
⇒ 4a2 + d2 = 120
⇒ a2 + 5d2 = 30
⇒ 25 + 5d2 = 30 [∵ a = 5]
⇒ 5d2 = 5 ⇒ d = ± 1
If d = 1, then the numbers are 2, 4, 6, 8.
If d = – 1, then the numbers are 8, 6, 4, 2. Thus, the numbers are 2, 4, 6, 8 or 8, 6, 4, 2.
Example 3: Divide 32 into four parts which are in A.P. such that the product of extremes is to the product of means is 7 : 15.
Solution. Let the four parts be (a – 3d), (a – d), (a + d) and (a + 3d). Then,
Sum = 32
⇒ (a – 3d) + (a – d) + (a + d) + (a + 3d) = 32
⇒ 4a = 32 ⇒ a = 8
It is given that
\( \frac{(a-3d)\,(a+3d)}{(a-d)\,(a+d)}=\frac{7}{15} \)
\( \frac{{{a}^{2}}-9{{d}^{2}}}{{{a}^{2}}-{{d}^{2}}}=\frac{7}{15}\text{ }\Rightarrow \text{ }\frac{64-9{{d}^{2}}}{64-{{d}^{2}}}=\frac{7}{15} \)
⇒ 128d2 = 512
⇒ d2 = 4 ⇒ d = ± 2
Thus, the four parts are a – d, a – d, a + d and
a + 3d i.e. 2, 6, 10 and 14.
Example 4: Find the sum of 20 terms of the A.P. 1, 4, 7, 10, ……
Solution. Let a be the first term and d be the common difference of the given A.P. Then, we have a = 1 and d = 3.
We have to find the sum of 20 terms of the given A.P.
Putting a = 1, d = 3, n = 20 in
Sn = \(\frac { n }{ 2 }\) [2a + (n – 1) d], we get
S20 = \(\frac { 20 }{ 2 }\) [2 × 1 + (20 – 1) × 3]
= 10 × 59 = 590
Example 5: Find the sum of first 30 terms of an A.P. whose second term is 2 and seventh term is 22.
Solution. Let a be the first term and d be the common difference of the given A.P. Then,
a2 = 2 and a7 = 22
⇒ a + d = 2 and a + 6d = 22
Solving these two equations, we get
a = – 2 and d = 4.
Sn = \(\frac { n }{ 2 }\) [2a + (n – 1) d]
∴ S30 = \(\frac { 30 }{ 2 }\) [2 × (–2) + (30 – 1) × 4]
⇒ 15 (–4 + 116) = 15 × 112
= 1680
Hence, the sum of first 30 terms is 1680.
Example 6: Find the sum of all natural numbers between 250 and 1000 which are exactly divisible by 3.
Solution. Clearly, the numbers between 250 and 1000 which are divisible by 3 are 252, 255, 258, …., 999. This is an A.P. with first term
a = 252, common difference = 3 and last term = 999. Let there be n terms in this A.P. Then,
⇒ an = 999
⇒ a + (n – 1)d = 999
⇒ 252 + (n – 1) × 3 = 999 ⇒ n = 250
∴ Required sum = Sn = \(\frac { n }{ 2 }\) [a + l]
= \(\frac { 250 }{ 2 }\) [252 + 999] = 156375
Example 7: How many terms of the series 54, 51, 48, …. be taken so that their sum is 513 ? Explain the double answer.
Solution. ∵ a = 54, d = – 3 and Sn = 513
⇒ \(\frac { n }{ 2 }\) [2a + (n – 1) d] = 513
⇒ \(\frac { n }{ 2 }\) [108 + (n – 1) × – 3] = 513
⇒ n2 – 37n + 342 = 0
⇒ (n – 18) (n – 19) = 0 ⇒ n = 18 or 19
Here, the common difference is negative, So, 19th term is a19 = 54 + (19 – 1) × – 3 = 0.
Thus, the sum of 18 terms as well as that of 19 terms is 513.
Example 8: If the mth term of an A.P. is 1/n and the nth term is 1/m, show that the sum of mn terms is (mn + 1).
Solution. Let a be the first term and d be the common difference of the given A.P. Then,
\( {{a}_{m}}=\frac{1}{n}\Rightarrow a+(m-1)d=\frac{1}{n}\text{ }……\text{ (i)} \)
\( {{a}_{n}}=\frac{1}{n}\Rightarrow a+(n-1)d=\frac{1}{n}\text{ }……\text{ (ii)} \)
Subtracting equation (ii) from equation (i), we get
\( (m-n)d=\frac{1}{n}-\frac{1}{m} \)
\( \Rightarrow (m-n)d=\frac{m-n}{mn}\Rightarrow d=\frac{1}{mn} \)
Putting d = 1/mn in equation (i), we get
\( a+(m-1)\frac{1}{mn}=\frac{1}{n} \)
\( \Rightarrow a+\frac{1}{n}-\frac{1}{mn}=\frac{1}{n}\Rightarrow a=\frac{1}{mn} \)
\( Now,{{S}_{mn}}=\frac{mn}{2}\left\{ 2a+\left( mn1 \right)\times d \right\} \)
\( {{S}_{mn}}=\frac{mn}{2}\left[ \frac{2}{mn}+(mn-1)\times \frac{1}{mn} \right] \)
\( {{S}_{mn}}=\frac{1}{2}\left( mn+1 \right)~~ \)
Example 9: If the term of m terms of an A.P. is the same as the sum of its n terms, show that the sum of its (m + n) terms is zero.
Solution. Let a be the first term and d be the common difference of the given A.P. Then,
Sm = Sn
⇒ \(\frac { m }{ 2 }\) [2a + (m – 1) d] = \(\frac { n }{ 2 }\) [2a + (n – 1) d]
⇒ 2a(m – n) + {m (m – 1) – n (n – 1)} d = 0
⇒ 2a (m – n) + {(m2 – n2) – (m – n)} d = 0
⇒ (m – n) [2a + (m + n – 1) d] = 0
⇒ 2a + (m + n – 1) d = 0
⇒ 2a + (m + n – 1) d = 0 [∵ m – n ≠ 0] ….(i)
\( {{S}_{m+n}}=\frac{m+n}{2}\left\{ 2a+\left( m+n-1 \right)d \right\} \)
\( {{S}_{m+n}}=\frac{m+n}{2}\times 0=0\text{ }\left[ \text{Using equation }\left( \text{i} \right) \right] \)
Example 10: The sum of n, 2n, 3n terms of an A.P. are S1, S2, S3 respectively. Prove that S3 = 3(S2 – S1).
Solution. Let a be the first term and d be the common difference of the given A.P. Then,
S1 = Sum of n terms
⇒ S1 = \(\frac { n }{ 2 }\) {2a + (n – 1)d} ….(i)
S2 = Sum of 2n terms
⇒ S2 = \(\frac { 2n }{ 2 }\) [2a + (2n – 1) d] ….(ii)
and, S3 = Sum of 3n terms
⇒ S3 = \(\frac { 3n }{ 2 }\) [2a + (3n – 1) d] ….(iii)
Now, S2 – S1
= \(\frac { 2n }{ 2 }\) [2a + (2n – 1) d] – \(\frac { n }{ 2 }\) [2a + (n –1) d]
S2 – S1 = \(\frac { n }{ 2 }\) [2 {2a + (2n – 1)d} – {2a + (n – 1)d}]
= \(\frac { n }{ 2 }\) [2a + (3n – 1) d]
∴ 3(S2 – S1) = \(\frac { 3n }{ 2 }\) [2a + (3n – 1) d] = S3 [Using (iii)]
Hence, S3 = 3 (S2 – S1)
Example 11: The sum of n terms of three arithmetical progression are S1, S2 and S3. The first term of each is unity and the common differences are
1, 2 and 3 respectively. Prove that S1 + S3 = 2S2.
Solution. We have,
S1 = Sum of n terms of an A.P. with first term 1 and common difference 1
= \(\frac { n }{ 2 }\) [2 × 1 + (n – 1) 1] = \(\frac { n }{ 2 }\) [n + 1]
S2 = Sum of n terms of an A.P. with first term 1 and common difference 2
= \(\frac { n }{ 2 }\) [2 × 1 + (n – 1) × 2] = n2
S3 = Sum of n terms of an A.P. with first term 1 and common difference 3
= \(\frac { n }{ 2 }\) [2 × 1 + (n – 1) × 3] = \(\frac { n }{ 2 }\) (3n – 1)
Now, S1 + S3 = \(\frac { n }{ 2 }\) (n + 1) + \(\frac { n }{ 2 }\) (3n – 1)
= 2n2 and S2 = n2
Hence S1 + S3 = 2S2
Example 12: The sum of the first p, q, r terms of an A.P. are a, b, c respectively. Show that
\(\frac { a }{ p }\) (q – r) + \(\frac { b }{ q }\) (r – p) + \(\frac { c }{ r }\) (p – q) = 0
Solution. Let A be the first term and D be the common difference of the given A.P. Then,
a = Sum of p terms ⇒ a = \(\frac { p }{ 2 }\) [2A + (q – 1) D]
⇒ \(\frac { 2a }{ p }\) = [2A + (p – 1) D] ….(i)
b = Sum of q terms
⇒ b = \(\frac { q }{ 2 }\) [2A + (q – 1) D]
⇒ \(\frac { 2b }{ q }\) = [2A + (q – 1) D] ….(ii)
and, c = Sum of r terms
⇒ c = \(\frac { r }{ 2 }\) [2A + (r – 1) D]
⇒ \(\frac { 2c }{ r }\) = [2A + (r – 1) D] ….(iii)
Multiplying equations (i), (ii) and (iii) by (q – r), (r – p) and (p – q) respectively and adding, we get
\(\frac { 2a }{ p }\) (q – r) + \(\frac { 2b }{ q }\) (r – p) + \(\frac { 2c }{ r }\) (p – q)
= [2A + (p – 1) D] (q – r) + [2A + (q – 1) D] (r – p) + [(2A + (r – 1) D] (p – q)
= 2A (q – r + r – p + p – q) + D [(p – 1) (q – r) + (q – 1)(r – p) + (r – 1) (p – q)]
= 2A × 0 + D × 0 = 0
Example 13: The ratio of the sum use of n terms of two A.P.’s is (7n + 1) : (4n + 27). Find the ratio of their mth terms.
Solution. Let a1, a2 be the first terms and d1, d2 the common differences of the two given A.P.’s .Then the sums of their n terms are given by
Sn = \(\frac { n }{ 2 }\) [21 + (n – 1) d1], and Sn‘ = \(\frac { n }{ 2 }\) [2a2 + (n – 1) d2]
\( \therefore \frac{{{S}_{n}}}{S_{n}^{‘}}=\frac{\frac{n}{2}[2{{a}_{1}}+(n-1){{d}_{1}}]}{\frac{n}{2}[2{{a}_{2}}+(n-1){{d}_{2}}]}=\frac{2{{a}_{1}}+(n-1){{d}_{1}}}{2{{a}_{2}}+(n-1){{d}_{2}}} \)
It is given that
\( \frac{{{S}_{n}}}{S_{n}^{‘}}=\frac{7n+1}{4n+27} \)
\( \Rightarrow \frac{2{{a}_{1}}+(n-1){{d}_{1}}}{2{{a}_{2}}+(n-1){{d}_{2}}}=\frac{7n+1}{4n+27} \)
To find the ratio of the mth terms of the two given A.P.’s, we replace n by (2m – 1) in equation (i). Then we get
\( \therefore \frac{2{{a}_{1}}+(2m-2){{d}_{1}}}{2{{a}_{2}}+(2m-2){{d}_{2}}}=\frac{7(2m-1)+1}{4(2m-1)+27} \)
\( \Rightarrow \frac{{{a}_{1}}+(m-1){{d}_{1}}}{{{a}_{2}}+(m-1){{d}_{2}}}=\frac{14m-6}{8m+23} \)
Hence the ratio of the mth terms of the two A.P.’s is (14m – 6) : (8m + 23)
More examples on Arithmetic Progression
Example 14: The ratio of the sums of m and n terms of an A.P. is m2 : n2. Show that the ratio of the mth and nth terms is (2m – 1) : (2n – 1).
Solution. Let a be the first term and d the common difference of the given A.P. Then, the sums of m and n terms are given by
Sm = \(\frac { m }{ 2 }\) [2a + (m – 1) d], and Sn = \(\frac { n }{ 2 }\) [2a + (n – 1) d]
respectively. Then,
\( \frac{{{S}_{m}}}{{{S}_{n}}}=\frac{{{m}^{2}}}{{{n}^{2}}}\Rightarrow \frac{\frac{m}{2}[2a+(m-1)d]}{\frac{n}{2}[2a+(n-1)d]}=\frac{{{m}^{2}}}{{{n}^{2}}} \)
\( \Rightarrow \frac{2a+(m-1)d}{2a+(n-1)d}=\frac{m}{n} \)
⇒ [2a + (m – 1) d] n = {2a + (n – 1) d} m
⇒ 2a (n – m) = d {(n – 1) m – (m – 1) n}
⇒ 2a (n – m) = d (n – m)
⇒ d = 2a
\( \text{Now, }\frac{{{T}_{m}}}{{{T}_{n}}}=\frac{a+(m-1)d}{a+(n-1)d} \)
\( =\frac{a+(m-1)2a}{a+(n-1)2a}=\frac{2m-1}{2n-1} \)