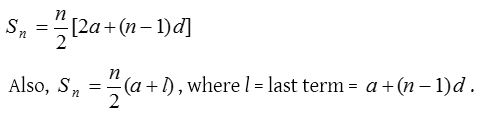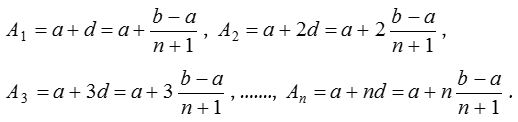Arithmetic Progression

Selina Concise Mathematics Class 10 ICSE Solutions Arithmetic Progression

Selina Publishers Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression

Arithmetic Progression Exercise 10A – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.

Solution:

Question 2.
The nth term of sequence is (2n – 3), find its fifteenth term.
Solution:

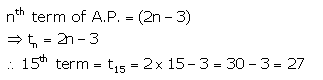
Question 3.
If the pth term of an A.P. is (2p + 3), find the A.P.
Solution:

Question 4.
Find the 24th term of the sequence:
12, 10, 8, 6,……
Solution:

Question 5.

Solution:

Question 6.

Solution:

Question 7.

Solution:

Question 8.
Is 402 a term of the sequence :
8, 13, 18, 23,………….?
Solution:

Question 9.

Solution:

Question 10.

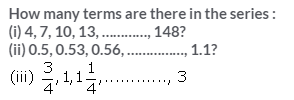
Solution:

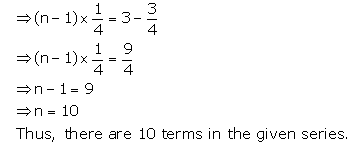
Question 11.
Which term of the A.P. 1 + 4 + 7 + 10 + ………. is 52?
Solution:

Question 12.
If 5th and 6th terms of an A.P are respectively 6 and 5. Find the 11th term of the A.P
Solution:

Question 13.

Solution:

Question 14.
Find the 10th term from the end of the A.P. 4, 9, 14,…….., 254
Solution:

Question 15.
Determine the arithmetic progression whose 3rd term is 5 and 7th term is 9.
Solution:

Question 16.
Find the 31st term of an A.P whose 10th term is 38 and 10th term is 74.
Solution:

Question 17.
Which term of the services :
21, 18, 15, …………. is – 81?
Can any term of this series be zero? If yes find the number of term.
Solution:

Question 18.
An A.P. consists of 60 terms. If the first and the last terms be 7 and 125 respectively, find the 31^st term.
Solution:
For a given A.P.,
Number of terms, n = 60
First term, a = 7
Last term, l = 125
⇒ t₆₀ = 125
⇒ a + 59d = 125
⇒ 7 + 59d = 125
⇒ 59d = 118
⇒ d = 2
Hence, t₃₁ = a + 30d = 7 + 30(2) = 7 + 60 = 67

Question 19.
The sum of the 4^th and the 8^th terms of an A.P. is 24 and the sum of the sixth term and the tenth term is 34. Find the first three terms of the A.P.
Solution:
Let ‘a’ be the first term and ‘d’ be the common difference of the given A.P.
t₄ + t₈ = 24 (given)
⇒ (a + 3d) + (a + 7d) = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12 ….(i)
And,
t₆ + t₁₀ = 34 (given)
⇒ (a + 5d) + (a + 9d) = 34
⇒ 2a + 14d = 34
⇒ a + 7d = 17 ….(ii)
Subtracting (i) from (ii), we get
2d = 5

Question 20.
If the third term of an A.P. is 5 and the seventh terms is 9, find the 17^th term.
Solution:
Let ‘a’ be the first term and ‘d’ be the common difference of the given A.P.
Now, t₃ = 5 (given)
⇒ a + 2d = 5 ….(i)
And,
t₇ = 9 (given)
⇒ a + 6d = 9 ….(ii)
Subtracting (i) from (ii), we get
4d = 4
⇒ d = 1
⇒ a + 2(1) = 5
⇒ a = 3
Hence, 17^th term = t₁₇ = a + 16d = 3 + 16(1) = 19

Arithmetic Progression Exercise 10B – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
In an A.P., ten times of its tenth term is equal to thirty times of its 30th term. Find its 40th term.
Solution:

Question 2.
How many two-digit numbers are divisible by 3?
Solution:

Question 3.
Which term of A.P. 5, 15, 25 ………… will be 130 more than its 31st term?
Solution:

Question 4.
Find the value of p, if x, 2x + p and 3x + 6 are in A.P
Solution:

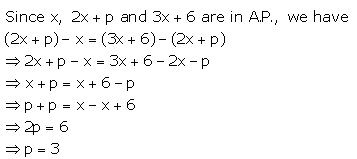
Question 5.
If the 3rd and the 9th terms of an arithmetic progression are 4 and -8 respectively, Which term of it is zero?
Solution:

Question 6.
How many three-digit numbers are divisible by 87?
Solution:

Question 7.
For what value of n, the nth term of A.P 63, 65, 67, …….. and nth term of A.P. 3, 10, 17,…….. are equal to each other?
Solution:

Question 8.
Determine the A.P. Whose 3rd term is 16 and the 7th term exceeds the 5th term by 12.
Solution:

Question 9.
If numbers n – 2, 4n – 1 and 5n + 2 are in A.P. find the value of n and its next two terms.
Solution:

Question 10.

Solution:

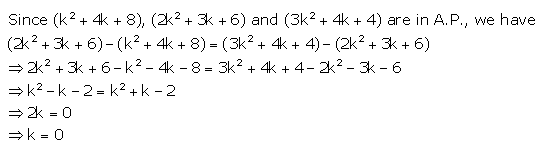
Question 11.
If a, b and c are in A.P show that:
(i) 4a, 4b and 4c are in A.P
(ii) a + 4, b + 4 and c + 4 are in A.P.
Solution:

Question 12.
An A.P consists of 57 terms of which 7th term is 13 and the last term is 108. Find the 45th term of this A.P.
Solution:

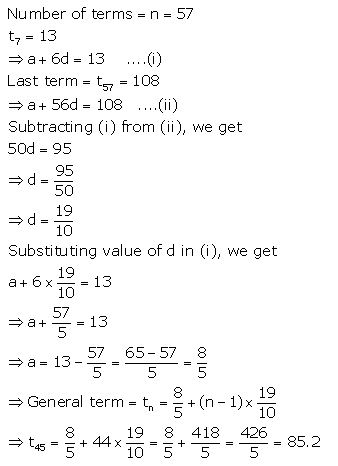
Question 13.
4th term of an A.P is equal to 3 times its first term and 7th term exceeds twice the 3rd time by I. Find the first term and the common difference.
Solution:

Question 14.
The sum of the 2nd term and the 7th term of an A.P is 30. If its 15th term is 1 less than twice of its 8th term, find the A.P
Solution:

Question 15.
In an A.P, if mth term is n and nth term is m, show that its rth term is (m + n – r)
Solution:

Question 16.
Which term of the A.P 3, 10, 17, ………. Will be 84 more than its 13th term?
Solution:

Arithmetic Progression Exercise 10C – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Find the sum of the first 22 terms of the A.P.: 8, 3, -2, ………..
Solution:

Question 2.
How many terms of the A.P. :
24, 21, 18, ……… must be taken so that their sum is 78?
Solution:

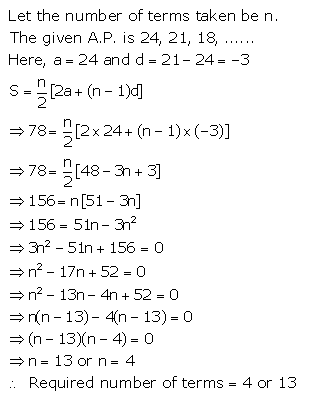
Question 3.
Find the sum of 28 terms of an A.P. whose nth term is 8n – 5.
Solution:

Question 4(i).
Find the sum of all odd natural numbers less than 50
Solution:

Question 4(ii).
Find the sum of first 12 natural numbers each of which is a multiple of 7.
Solution:

Question 5.
Find the sum of first 51 terms of an A.P. whose 2nd and 3rd terms are 14 and 18 respectively.
Solution:

Question 6.
The sum of first 7 terms of an A.P is 49 and that of first 17 terms of it is 289. Find the sum of first n terms
Solution:

Question 7.
The first term of an A.P is 5, the last term is 45 and the sum of its terms is 1000. Find the number of terms and the common difference of the A.P.
Solution:

Question 8.
Find the sum of all natural numbers between 250 and 1000 which are divisible by 9.
Solution:

Question 9.
The first and the last terms of an A.P. are 34 and 700 respectively. If the common difference is 18, how many terms are there and what is their sum?
Solution:

Question 10.
In an A.P, the first term is 25, nth term is -17 and the sum of n terms is 132. Find n and the common difference.
Solution:

Question 11.
If the 8th term of an A.P is 37 and the 15th term is 15 more than the 12th term, find the A.P. Also, find the sum of first 20 terms of A.P.
Solution:

Question 12.
Find the sum of all multiples of 7 between 300 and 700.
Solution:

Question 13.

Solution:

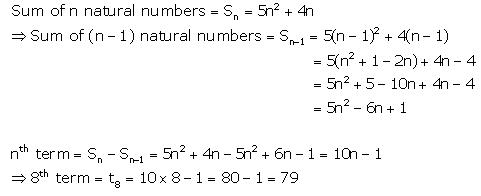
Question 14.
The fourth term of an A.P. is 11 and the term exceeds twice the fourth term by 5 the A.P and the sum of first 50 terms
Solution:

Arithmetic Progression Exercise 10D – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Find three numbers in A.P. whose sum is 24 and whose product is 440.
Solution:

Question 2.
The sum of three consecutive terms of an A.P. is 21 and the slim of their squares is 165. Find these terms.
Solution:

Question 3.
The angles of a quadrilateral are in A.P. with common difference 20°. Find its angles.
Solution:

Question 4.
Divide 96 into four parts which are in A.P. and the ratio between product of their means to product of their extremes is 15 : 7.
Solution:

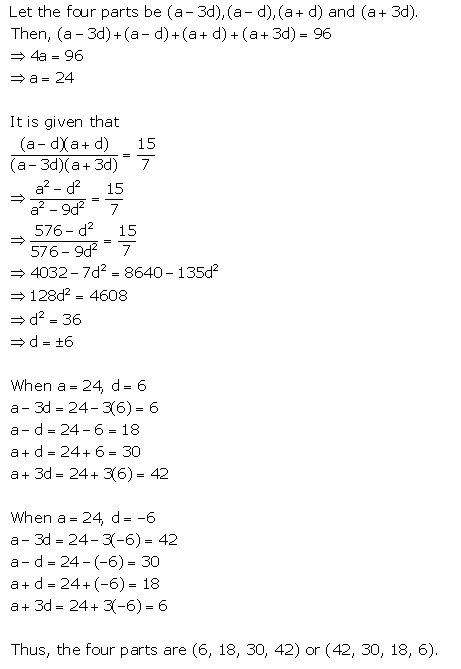
Question 5.
Find five numbers in A.P. whose sum is \(12 \frac{1}{2}\) and the ratio of the first to the last terms is 2: 3.
Solution:

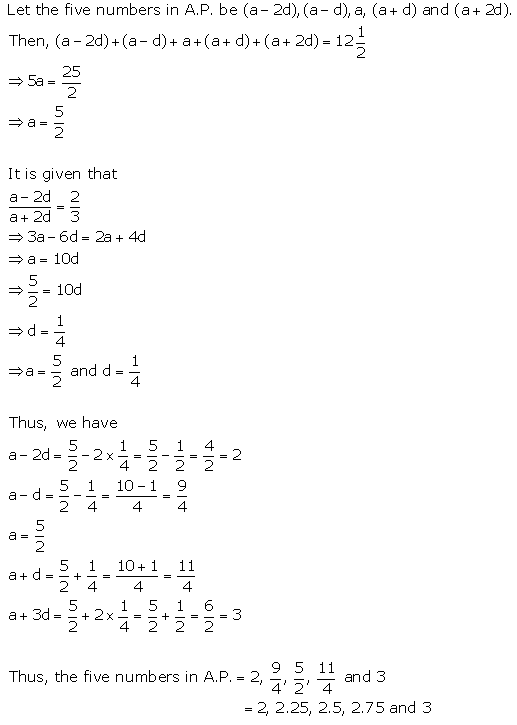
Question 6.
Split 207 into three parts such that these parts are in A.P. and the product of the two smaller parts is 4623.
Solution:

Question 7.
The sum of three numbers in A.P. is 15 the sum of the squares of the extreme is 58. Find the numbers.
Solution:

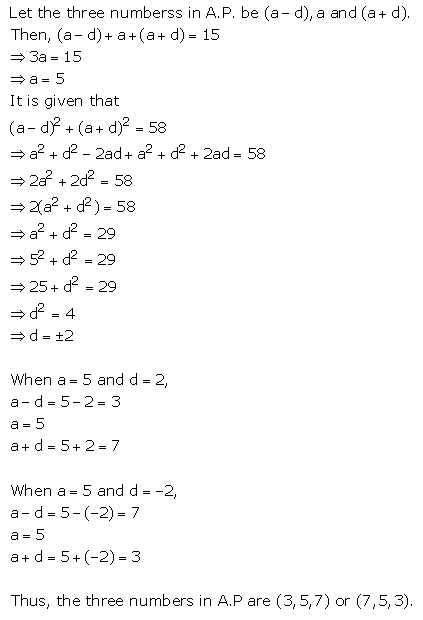
Question 8.
Find four numbers in A.P. whose sum is 20 and the sum of whose squares is 120.
Solution:

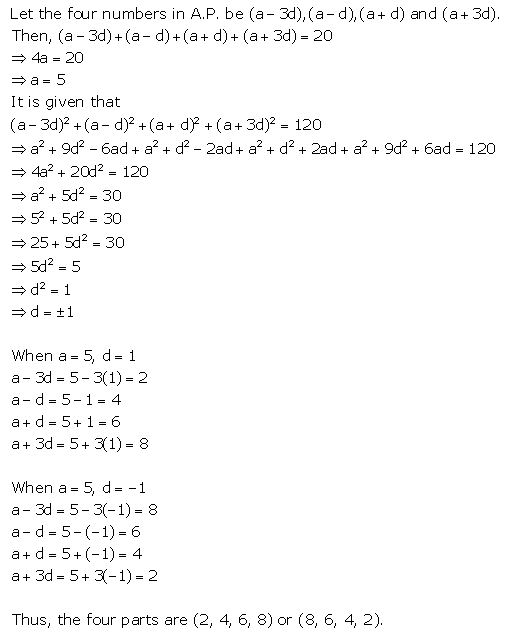
Question 9.
Insert one arithmetic mean between 3 and 13.
Solution:

Question 10.
The angles of a polygon are in A.P. with common difference 5°. If the smallest angle is 120°, find the number of sides of the polygon.
Solution:

Question 11.
\(\frac{1}{a}, \frac{1}{b} \text { and } \frac{1}{c}\) are in A.P. Show that : be, ca and ab are also in A.P.
Solution:

Question 12.
Insert four A.M.s between 14 and -1.
Solution:

Question 13.
Insert five A.M.s between -12 and 8.
Solution:

Question 14.
Insert six A.M.s between 15 and -15.
Solution:

Arithmetic Progression Exercise 10E – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
Two cars start together in the same direction from the same place. The first car goes at uniform speed of 10 km hr^-1 The second car goes at a speed of 8 km h^-1 in the first hour and thereafter increasing the speed by 0.5 km h^-1 each succeeding hour. After how many hours will the two cars meet?
Solution:

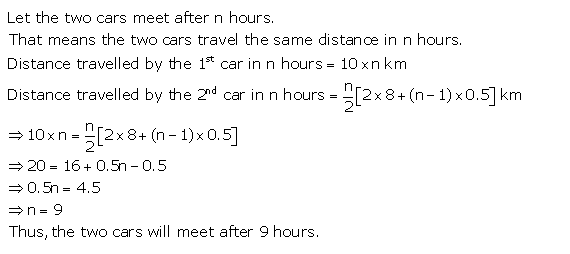
Question 2.
A sum of ₹ 700 is to be paid to give seven cash prizes to the students of a school for their overall academic performance. If the cost of each prize is ₹ 20 less than its preceding prize; find the value of each of the prizes.
Solution:

Question 3.
An article can be bought by paying ₹ 28,000 at once or by making 12 monthly instalments. If the first instalment paid is ₹ 3,000 and every other instalment is ₹ 100 less than the previous one, find :
(i) amount of instalment paid in the 9th month
(ii) total amount paid in the instalment scheme.
Solution:

Question 4.
A manufacturer of TV sets produces 600 units in the third year and 700 units in the 7^th year.
Assuming that the production increases uniformly by a fixed number every year, find :
(i) the production in the first year.
(ii) the production in the 10^th year.
(iii) the total production in 7 years.
Solution:

Question 5.
Mrs. Gupta repays her total loan of ₹ 1.18,000 by paying instalments every month. If the instalment for the first month is ₹ 1,000 and it increases by ₹ 100 every month, what amount will she pay as the 30^th instalment of loan? What amount of loan she still has to pay after the 30^th instalment?
Solution:

Question 6.
In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be five times of the class to which the respective section belongs. If there are 1 to 10 classes in the school and each class has three sections, find how many trees were planted by the students?
Solution:

Arithmetic Progression Exercise 10F – Selina Concise Mathematics Class 10 ICSE Solutions

Question 1.
The 6^th term of an A.P. is 16 and the 14^th term is 32. Determine the 36^th term.
Solution:
Let ‘a’ be the first term and ‘d’ be the common difference of the given A.P.
Now, t₆ = 16 (given)
⇒ a + 5d = 16 ….(i)
And,
t₁₄ = 32 (given)
⇒ a + 13d = 32 ….(ii)
Subtracting (i) from (ii), we get
8d = 16
⇒ d = 2
⇒ a + 5(2) = 16
⇒ a = 6
Hence, 36^th term = t₃₆ = a + 35d = 6 + 35(2) = 76

Question 2.
If the third and the 9^th terms of an A.P. term is 12 and the last term is 106. Find the 29^th term of the A.P.
Solution:
For an A.P.,a
t₃ = 4
⇒ a + 2d = 4 … (i)
t₉ = -8
⇒ a + 8d = -8 …. (ii)
Subtracting (i) from (ii), we get
6d = -12
⇒ d = -2
Substituting d = -2 in (i), we get
a = 2(-2) = 4
⇒ a – 4 = 4
⇒ a = 8
⇒ General term = t_n = 8 + (n – 1)(-2)
Let p^th term of this A.P. be 0.
⇒ 8 + (0 – 1) (-2) = 0
⇒ 8 – 2p + 2 = 0
⇒ 10 – 2p = 0
⇒ 2p = 10
⇒ p = 5
Thus, 5^th term of this A.P. is 0.

Question 3.
An A.P. consists of 50 terms of which 3^rd term is 12 and the last term is 106. Find the 29^th term of the A.P.
Solution:
For a given A.P.,
Number of terms, n = 50
3^rd term, t₃ = 12
⇒ a + 2d = 12 ….(i)
Last term, l = 106
⇒ t₅₀ = 106
⇒ a + 49d = 106 ….(ii)
Subtracting (i) from (ii), we get
47d = 94
⇒ d = 2
⇒ a + 2(2) = 12
⇒ a = 8
Hence, t₂₉ = a + 28d = 8 + 28(2) = 8 + 56 = 64

Question 4.
Find the arithmetic mean of :
(i) -5 and 41
(ii) 3x – 2y and 3x + 2y
(iii) (m + n)² and (m – n)²
Solution:

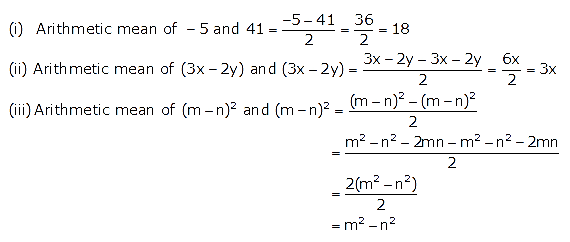
Question 5.
Find the sum of first 10 terms of the A.P. 4 + 6 + 8 + ………
Solution:
Here,
First term, a = 4
Common difference, d = 6 – 4 = 2
n = 10

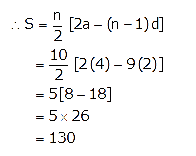
Question 6.
Find the sum of first 20 terms of an A.P. whose first term is 3 and the last term is 60.
Solution:
Here,
First term, a = 3
Last term, l = 57
n = 20

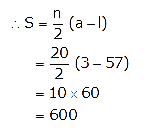
Question 7.
How many terms of the series 18 + 15 + 12 + ……. when added together will give 45 ?
Solution:
Here, we find that
15 – 18 = 12 – 15 = -3
Thus, the given series is an A.P. with first term 18 and common difference -3.
Let the number of term to be added be ‘n’.

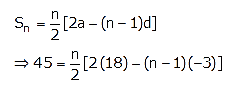
⇒ 90 = n[36 – 3n + 3]
⇒ 90 = n[39 – 3n]
⇒ 90 = 3n[13 – n]
⇒ 30 = 13n – n²
⇒ n² – 13n + 30 = 0
⇒ n² – 10n – 3n + 30 = 0
⇒ n(n – 10) – 3(n – 10) = 0
⇒ (n – 10)(n – 3) = 0
⇒ n – 10 = 0 or n – 3 = 0
⇒ n = 10 or n = 3
Thus, required number of term to be added is 3 or 10.

Question 8.
The n^th term of a sequence is 8 – 5n. Show that the sequence is an A.P.
Solution:
t_n = 8 – 5n
Replacing n by (n + 1), we get
t_n+1 = 8 – 5(n + 1) = 8 – 5n – 5 = 3 – 5n
Now,
t_n+1 – t_n = (3 – 5n) – (8 – 5n) = -5
Since, (t_n+1 – t₂) is independent of n and is therefore a constant.
Hence, the given sequence is an A.P.

Question 9.
The the general term (n^th term) and 23^rd term of the sequence 3, 1, -1, -3, ……
Solution:
The given sequence is 1, -1, -3, …..
Now,
1 – 3 = -1 – 1 = -3 – (-1) = -2
Hence, the given sequence is an A.P. with first term a = 3 and common difference d = -2.
The general term (n^th term) of an A.P. is given by
t_n = a + (n – 1)d
= 3 + (n – 1)(-2)
= 3 – 2n + 2
= 5 – 2n
Hence, 23^rd term = t₂₃ = 5 – 2(23) = 5 – 46 = -41

Question 10.
Which term of the sequence 3, 8, 13, …….. is 78 ?
Solution:
The given sequence is 3, 8, 13, …..
Now,
8 – 3 = 13 – 8 = 5
Hence, the given sequence is an A.P. with first term a = 3 and common difference d = 5.
Let the n^th term of the given A.P. be 78.
⇒ 78 = 3 + (n – 1)(5)
⇒ 75 = 5n – 5
⇒ 5n = 80
⇒ n = 16
Thus, the 16th term of the given sequence is 78.

Question 11.
Is -150 a term of 11, 8, 5, 2, ……… ?
Solution:
The given sequence is 11, 8, 5, 2, …..
Now,
8 – 11 = 5 – 8 = 2 – 5 = -3
Hence, the given sequence is an A.P. with first term a = 11 and common difference d = -3.
The general term of an A.P. is given by
t_n = a + (n – 1)d
⇒ -150 = 11 + (n – 1)(-5)
⇒ -161 = -5n + 5
⇒ 5n = 166
⇒ n =\(\frac{166}{5}\)
The number of terms cannot be a fraction.
So, clearly, -150 is not a term of the given sequence.

Question 12.
How many two digit numbers are divisible by 3 ?
Solution:
The two-digit numbers divisible by 3 are as follows: 12, 15, 18, 21, …….. 99
Clearly, this forms an A.P. with first term, a = 12
and common difference, d = 3
Last term = n^th term= 99
The general term of an A.P. is given by
t_n = a + (n – 1)d
⇒ 99 – 12 + (n – 1)(3)
⇒ 99 – 12 + 3n-3
⇒ 90 – 3n
⇒ n = 30
Thus, 30 two-digit numbers are divisible by 3.

Question 13.
How many multiples of 4 lie between 10 and 250 ?
Solution:
Numbers between 10 and 250 which are multiple of 4 are as follows: 12, 16, 20, 24,……, 248
Clearly, this forms an A.P. with first term a = 12,
common difference d= 4 and last term l = 248
l – a + (n – 1)d
⇒ 248 – 12 + (n – 1) × 4
⇒ 236 – (n – 1) × 4
⇒ n – 1 = 59
⇒ n = 60
Thus, 60 multiples of 4 lie between 10 and 250.

Question 14.
The sum of the 4^th term and the 8^th term of an A.P. is 24 and the sum of 6^th term and the 10^th term is 44. Find the first three terms of the A.P.
Solution:
Given, t₄ + t₈ = 24
(a + 3d) + (a + 7d) = 24
= 2a+ 10d = 24
> a + 5d = 12 ….(i)
And,
t₆₂ + t₁₀ = 44
= (a + 5d) + (a + 9d) = 44
= 2a+ 14d = 44
= a + 7 = 22 …(ii)
Subtracting (i) from (ii), we get
2d = 10
= d = 5
Substituting value of din (i), we get
a + 5 × 5 = 12
= a + 25 = 12
= a = -13 = 1^st term
a + d = -13 + 5 = -8 = 2^nd term
a + 2d = -13 + 2 × 5 = -13 + 10= -3 = 3^rd term
Hence, the first three terms of an A.P. are – 13,- 8 and -5.

Question 15.
The sum of first 14 terms of an A.P. is 1050 and its 14^th term is 140. Find the 20^th term.
Solution:
Let ‘a’ be the first term and ‘d’ be the common difference of the given A.P.
Given,
S₁₄= 1050
\(\frac{14}{2}[2 a+(14-1) d]=1050\)
⇒ 7[2a + 13d] = 1050
⇒ 2a + 13d = 150
⇒ a + 6.5d = 75 ….(i)
And, t₁₄ = 140
⇒ a + 13d = 140 ….(ii)
Subtracting (i) from (ii), we get
6.5d = 65
⇒ d = 10
⇒ a + 13(10) = 140
⇒ a = 10
Thus, 20^th term = t₂₀ = 10 + 19d = 10 + 19(10) = 200

Question 16.
The 25^th term of an A.P. exceeds its 9^th term by 16. Find its common difference.
Solution:
n^th term of an A.P. is given by tn= a + (n – 1) d.
⇒ t₂₅ = a + (25 – 1)d = a + 24d and
t₉ = a + (9 – 1)d = a + 8d
According to the condition in the question, we get
t₂₅ = t₉ + 16
⇒ a + 24d = a + 8d + 16
⇒ 16d = 16
⇒ d = 1

Question 17.
For an A.P., show that:
(m + n)^th term + (m – n)^th term = 2 × m^thterm
Solution:
Let a and d be the first term and common difference respectively.
⇒(m + n)^th term = a + (m + n – 1)d …. (i) and
(m – n)^th term = a + (m – n – 1)d …. (ii)
From (i) + (ii), we get
(m + n)^th term + (m – n)^th term
= a + (m + n – 1)d + a + (m – n – 1)d
= a + md + nd – d + a + md – nd – d
= 2a + 2md – 2d
= 2a + (m – 1)2d
= 2[ a + (m – 1)d]
= 2 × m^th term
Hence proved.

Question 18.
If the n^th term of the A.P. 58, 60, 62,…. is equal to the n^th term of the A.P. -2, 5, 12, …., find the value of n.
Solution:
In the first A.P. 58, 60, 62,….
a = 58 and d = 2
t_n = a + (n – 1)d
⇒ t_n = 58 + (n – 1)2 …. (i)
In the first A.P. -2, 5, 12, ….
a = -2 and d = 7
t_n = a + (n – 1)d
⇒ t_n = -2 + (n – 1)7 …. (ii)
Given that the n^th term of first A.P is equal to the n^th term of the second A.P.
⇒58 + (n – 1)2 = -2 + (n – 1)7 … from (i) and (ii)
⇒58 + 2n – 2 = -2 + 7n – 7
⇒ 65 = 5n
⇒ n = 15

Question 19.
Which term of the A.P. 105, 101, 97 … is the first negative term?
Solution:
Here a = 105 and d = 101 – 105 = -4
Let an be the first negative term.
⇒ a_2n < 0
⇒ a + (n – 1)d < 0
⇒ 105 + (n – 1)(-4)

Question 20.
How many three digit numbers are divisible by 7?
Solution:
The first three digit number which is divisible by 7 is 105 and the last digit which is divisible by 7 is 994.
This is an A.P. in which a = 105, d = 7 and t_n = 994.
We know that n^th term of A.P is given by
t_n = a + (n – 1)d.
⇒ 994 = 105 + (n – 1)7
⇒ 889 = 7n – 7
⇒ 896 = 7n
⇒ n = 128
∴ There are 128 three digit numbers which are divisible by 7.

Question 21.
Divide 216 into three parts which are in A.P. and the product of the two smaller parts is 5040.
Solution:
Let the three parts of 216 in A.P be (a – d), a, (a + d).
⇒a – d + a + a + d = 216
⇒ 3a = 216
⇒ a = 72
Given that the product of the two smaller parts is 5040.
⇒ a(a – d ) = 5040
⇒ 72(72 – d) = 5040
⇒ 72 – d = 70
⇒ d = 2
∴ a – d = 72 – 2 = 70, a = 72 and a + d = 72 + 2 = 74
Therefore the three parts of 216 are 70, 72 and 74.

Question 22.
Can 2n² – 7 be the n^th term of an A.P? Explain.
Solution:
We have 2n² – 7,
Substitute n = 1, 2, 3, … , we get
2(1)² – 7, 2(2)² – 7, 2(3)² – 7, 2(4)² – 7, ….
-5, 1, 11, ….
Difference between the first and second term = 1 – (-5) = 6
And Difference between the second and third term = 11 – 1 = 10
Here, the common difference is not same.
Therefore the nth term of an A.P can’t be 2n² – 7.

Question 23.
Find the sum of the A.P., 14, 21, 28, …, 168.
Solution:
Here a = 14 , d = 7 and t_n = 168
t_n = a + (n – 1)d
⇒ 168 = 14 + (n – 1)7
⇒ 154 = 7n – 7
⇒ 154 = 7n – 7
⇒ 161 = 7n
⇒ n = 23
We know that,

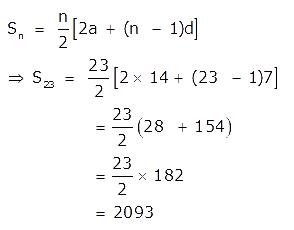
Therefore the sum of the A.P., 14, 21, 28, …, 168 is 2093.

Question 24.
The first term of an A.P. is 20 and the sum of its first seven terms is 2100; find the 31^st term of this A.P.
Solution:
Here a = 20 and S₇ = 2100
We know that,

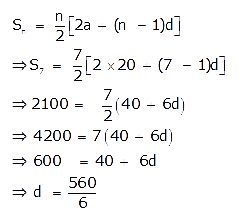
To find: t₃₁ =?
t_n = a + (n – 1)d

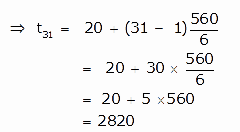
Therefore the 31st term of the given A.P. is 2820.

Question 25.
Find the sum of last 8 terms of the A.P. -12, -10, -8, ……, 58.
Solution:
First we will reverse the given A.P. as we have to find the sum of last 8 terms of the A.P.
58, …., -8, -10, -12.
Here a = 58 , d = -2

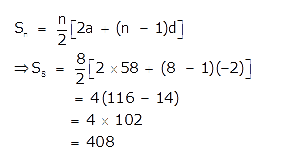
Therefore the sum of last 8 terms of the A.P. -12, -10, -8, ……, 58 is 408.

More Resources for Selina Concise Class 10 ICSE Solutions

• Selina ICSE Class 10 Maths Solutions
• Concise Physics Class 10 ICSE Answers
• Concise Chemistry Class 10 ICSE Answers
• Concise Biology Class 10 ICSE Answers

ICSE Solutions Selina ICSE Solutions