Pre Algebra

Addition and Subtraction of Decimals

by

Addition and Subtraction of Decimals

For addition/subtraction of decimals, we have to follow these steps:

Step 1: Change the given decimals into like decimals.
Step 2: Write the numbers in columns, so that decimal points should come in one column and tenths comes under tenths, hundredths comes under hundredths, and so on.
Step 3: Now, add or subtract the decimals, as we add or subtract the whole numbers.
Step 4: Put the decimal in the sum or difference directly under the decimal points of all the decimals.

Example 1: Add 3.85 and 2.5.
Solution: Converting into like decimals
Addition and Subtraction of Decimals 1
∴  3.85 + 2.5 = 6.35

Example 2: Subtract 41.715 from 63.2.
Solution: Converting into like decimals
Addition and Subtraction of Decimals 2
∴  63.2-41.715 = 21.485

Example 3: Add 41.8, 39.24, 5.01, and 62.6.
Solution: Converting into like decimals
Addition and Subtraction of Decimals 3
∴  41.8 + 39.24 + 5.01 + 62.6 = 148.65

Example 4: Surajgot Rs 15.50 from his mother and Rs 30.05 from his father. How much money did he get?
Solution:
Addition and Subtraction of Decimals 4
Example 5: The sum of two numbers is 100. If one of them is 78.67, find the other.
Solution:
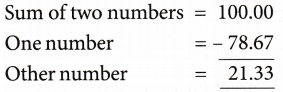
Addition and Subtraction of Decimals 5

Note:

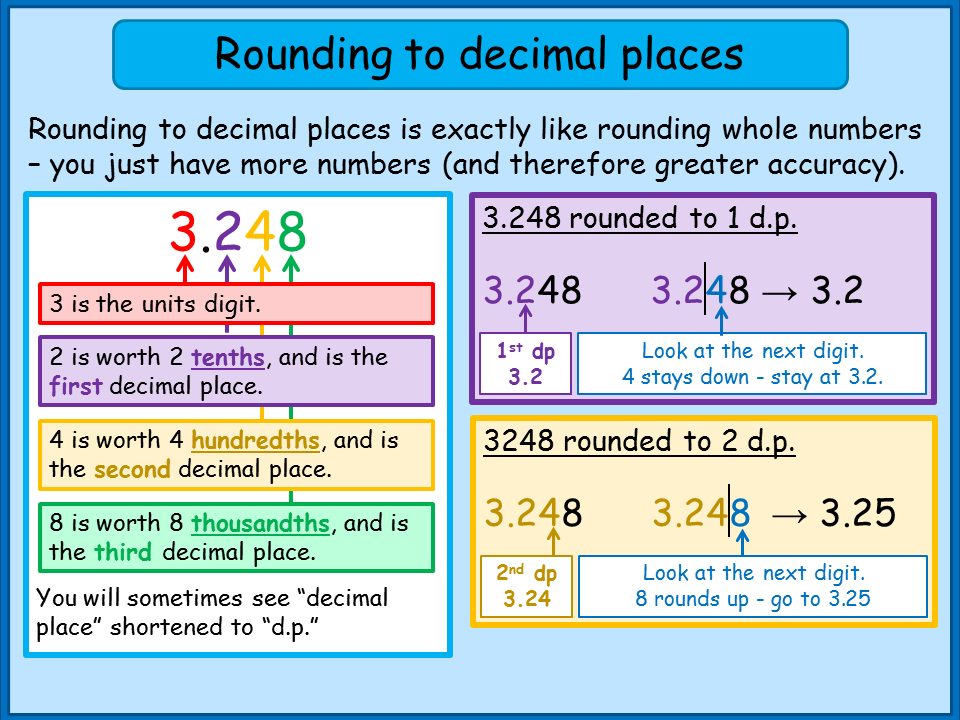
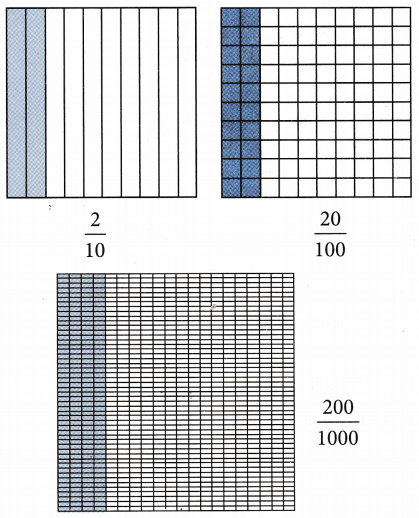
  • Fractions with denominators 10,100,1000, etc. are known as decimal fractions or decimals.
  • Decimal number has whole number part and decimal part separated by a decimal point.
  • Zeros to the extreme right side of the decimals does not have any value.
  • Two decimals having the same number of decimal places are like decimals and decimals having different decimal places are unlike decimals.
  • To add or subtract decimals, it is easier to convert them as like decimals and then add or subtract as we do for whole numbers.

Read More About:

Maths

How do you Convert Unlike Decimals into Like Decimals

by

How do you Convert Unlike Decimals into Like Decimals

Like decimals:
Decimals with the same number of decimal places are called like decimals.
Examples: 0.6, 3.5, 6.1 ( one decimal place)
2.15,0.78,26.11 (two decimal places)

Unlike decimals:
Decimals having different number of decimal places are called unlike decimals.
Examples: 0.7, 2.12, 6J25 are unlike decimals 3.12, 0.8, 13.856 are unlike decimals

Converting Unlike Decimals into Like Decimals

We can convert unlike decimals into like decimals by adding zeros to the right of decimal point or by finding their equivalent decimal.

Note:
Unlike decimals can also be equivalent decimals. Examples: 0.3, 0.30, 0.3000 are unlike but equivalent decimals.
Examples:
How do you Convert Unlike Decimals into Like Decimals 1
How do you Convert Unlike Decimals into Like Decimals 2

Comparing Decimals

To compare the decimals, we have to follow the following steps:

  1. Convert unlike decimals into like decimals.
  2. Compare the whole number part. The decimals with greater whole number part is greater.
  3. If the whole number part is equal, then compare the digits in the tenth place. The decimal with greater digit in the tenth place is greater.
  4. If digits in the tenth place are also equal, then compare the digits in the hundredth place and so on.

Example: Which decimal is greater, 78.40 or 78.216?
Solution:
Converting the given decimals into like decimals
78.40 = 78.400
78.216 = 78.216
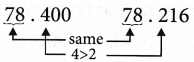
How do you Convert Unlike Decimals into Like Decimals 3
∴  78.400 >78.216
so, 78.40 >78.216

Read More About:

Maths

What is the Definition of an Equivalent Decimal

by

What is the Definition of an Equivalent Decimal

Equivalent Decimals

Decimals are a type of fractional number. The decimal 0.2 represents the fraction \(\frac{2}{10}\). We know \(\frac{2}{10}\) is equivalent to \(\frac{1}{5}\), since \(\frac{1}{5}\) times of \(\frac{2}{2}\) is \(\frac{2}{10}\).
Therefore, the decimal 0.2 is equivalent to \(\frac{1}{5}\) or \(\frac{2}{10}\) or \(\frac{20}{100}\) or \(\frac{200}{1000}\) etc.

Observe the following diagrammatic representation:
What is the Definition of an Equivalent Decimal 1
What is the Definition of an Equivalent Decimal 2
All these three decimals i.e., 0.2, 0.20, and 0.200, have the same value and so they are called equivalent decimals.
Example 1: Give next two decimal numbers in the sequence:
(a) 1.32, 1.42, 1.52, …, …
(b) 1.14,1.25, 1.36, …, …
Solution:
(a) 1.32,1.42,1.52,1.62,1.72
(b) 1.14,1.25,1.36,1.47,1.58

Writing or removing zeros at the end of the decimal does not change its value.
Examples
0. 5 =0.50 = 0.500
= 0.5000 = 0.50000
6.2 = 6.20 = 6.200
= 6.2000 = 6.2000

Example 2: Write the number name for 207.652.
Solution: 207.652 = Two hundred seven point six five two

Example 3: Write the decimal fraction 35.439 in expanded form.
Solution:
What is the Definition of an Equivalent Decimal 3

Read More About:

Maths

What is Fraction and How many Types of Fractions are there

by

What is Fraction and How many Types of Fractions are there

Fraction

A number that compares part of an object or a set with the whole, especially the quotient of two whole numbers is written in the form of xly is called a fraction. The fraction 1/3, which means 1 divided by 3, can be represented as 1 pencil out of a box of 3 pencils.
A fraction is a (i) part of a whole. (ii) part of a collection.

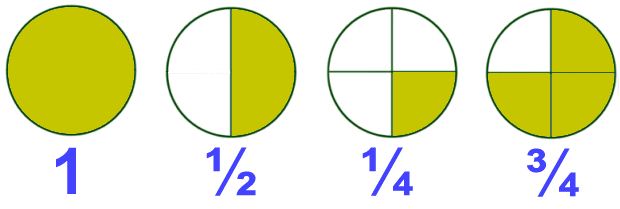
What is Fraction and How many Types of Fractions are there 1

A fraction comprises two numbers separated by a horizontal line. The number above-the horizontal line is called the numerator and the number below the horizontal line is called the denominator of the fraction.
What is Fraction and How many Types of Fractions are there 2

Fraction as a part of a whole
A fraction is a part of a whole. Imagine a pizza cut into slices. All of the slices make 1 whole pizza. Each slice is a fraction of a pizza.
Tanya and Sanya want to share a pizza equally
What is Fraction and How many Types of Fractions are there 3They decide to cut the pizza from the middle and divide it into two equal parts. Each part is called
the half of the whole and written as \(\frac{1}{2}\). Both the sisters get equal share. The \(\frac{1}{2}\) part of the whole is a fraction.
What is Fraction and How many Types of Fractions are there 4Similarly, we can take many examples from our daily life to show fraction as a part of a whole.
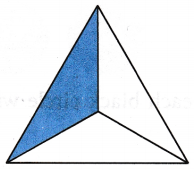What is Fraction and How many Types of Fractions are there54In this figure we have divided a triangle into 3 equal parts. The shaded part shows one part out of three, i.e., \(\frac{1}{3}\). Here, \(\frac{1}{3}\) is a fraction, which is a part of the whole triangle.

Read More:

Fraction is a part of a collection
A fraction represents parts of a collection, the numerator being the number of parts we have and the denominator being the total number of parts in the collection.
Let us take a collection of 12 stars and we want to shade \(\frac{3}{4}\) of the collection.
What is Fraction and How many Types of Fractions are there 6In order to find \(\frac{3}{4}\) out of the 12 stars, we divide the 12 stars into four equal parts.
What is Fraction and How many Types of Fractions are there 7Each part contains 3 stars. Now, we can shade 3 parts out of 4 parts.
What is Fraction and How many Types of Fractions are there 8On counting, we find that the total number of shaded stars is 9.
In other words, \(\frac{3}{4}\) of 12 stars = 9 stars.

Types of fractions

  1. Like fractions: Fractions having the same denominators are called like fractions.
    Examples: \(\frac{1}{7}\), \(\frac{3}{7}\), \(\frac{2}{7}\), \(\frac{6}{7}\) etc. are like fractions.
  2. Unlike fractions: Fractions having different denominators are called unlike fractions.
    Examples: \(\frac{2}{3}\), \(\frac{5}{7}\), \(\frac{6}{8}\), \(\frac{1}{3}\) etc. are unlike fractions.
  3. Unit fraction: A fraction having a numerator as 1 is called a unit fraction.
    Examples: \(\frac{1}{3}\), \(\frac{1}{9}\), \(\frac{1}{8}\), \(\frac{1}{5}\) etc. are all unit fractions
  4. Proper fraction: A fraction, whose numerator is smaller than its denominator is called a proper fraction.
    Examples: \(\frac{2}{3}\), \(\frac{5}{7}\), \(\frac{1}{6}\), \(\frac{3}{9}\) etc. are all proper fractions.
  5. Improper fraction: A fraction, whose numerator is greater than or equal to its denominator is called an improper fraction.
    Examples: \(\frac{4}{3}\), \(\frac{7}{5}\), \(\frac{9}{9}\) etc. are all improper fractions.
  6. Mixed fraction: A fraction, which is a combination of a whole number and a proper fraction is called a mixed fraction. All improper fractions can be written in the form of mixed fractions.
    Example: 2 \(\frac{1}{4}\) is a mixed fraction, since 2 is a 4 whole number and \(\frac{1}{4}\) is a proper fraction.
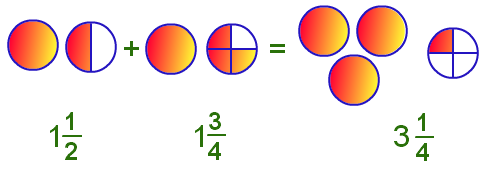
    What is Fraction and How many Types of Fractions are there 9
  7. Equivalent Fraction: If \(\frac { c }{ d } =\frac { m\times a }{ m\times b }\), then the fractions \(\frac{a}{b}\) and \(\frac{c}{d}\) are called equivalent fractions because they represent the same portion of the whole.
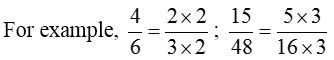
    What is Fraction and How many Types of Fractions are there 10
    For example, the shaded parts of each of the following figures are same but they are represented by different fractional numbers.
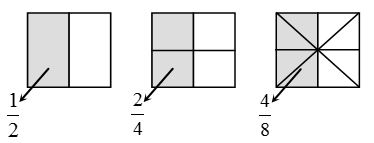
    What is Fraction and How many Types of Fractions are there 11
    They are called equivalent fractions.
    So we write \(\frac { 1 }{ 2 } =\frac { 2 }{ 4 } =\frac { 4 }{ 8 }\) , etc.
  8. Decimal fractions: A fraction whose denominator is any of the number 10,100,1000 etc. is called a decimal fraction.
    For example : \(\frac { 8 }{ 10 } ,\frac { 11 }{ 100 } ,\frac { 17 }{ 1000 }\) etc. are decimal fractions.
  9. Vulgar fractions: A fraction whose denominator is a whole number, other than 10,100,1000 etc. is called a vulgar fractions.
    For example \(\frac { 2 }{ 7 } ,\frac { 3 }{ 8 } ,\frac { 11 }{ 17 }\) etc. are vulgar fractions.

Maths

How do you Round to the Nearest Ten Thousand

by

How do you Round to the Nearest Ten Thousand

Rounding off numbers

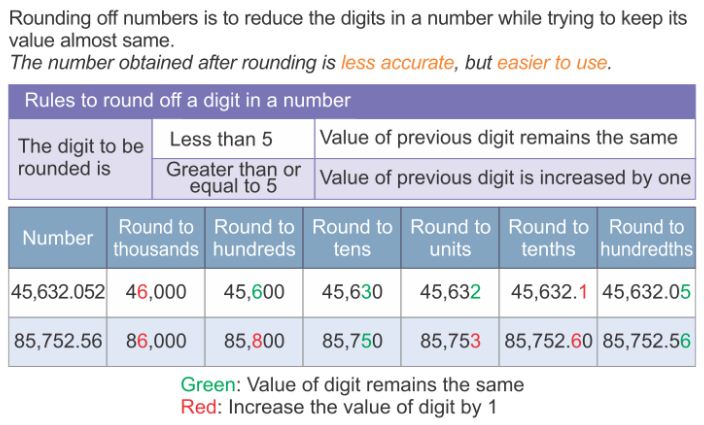
How do you Round to the Nearest Ten Thousand 1
We have already learnt rounding off the numbers to the nearest tens, hundreds, etc. Let us review them. Let us consider a number, say 12 on a number line. It lies between 10 and 20. We observe that the gap between 10 and 12 is less than the gap between 12 and 20, i.e., 12 is nearer to 10 than 20. So, we round off 12 to 10, that is, to the nearest ten.
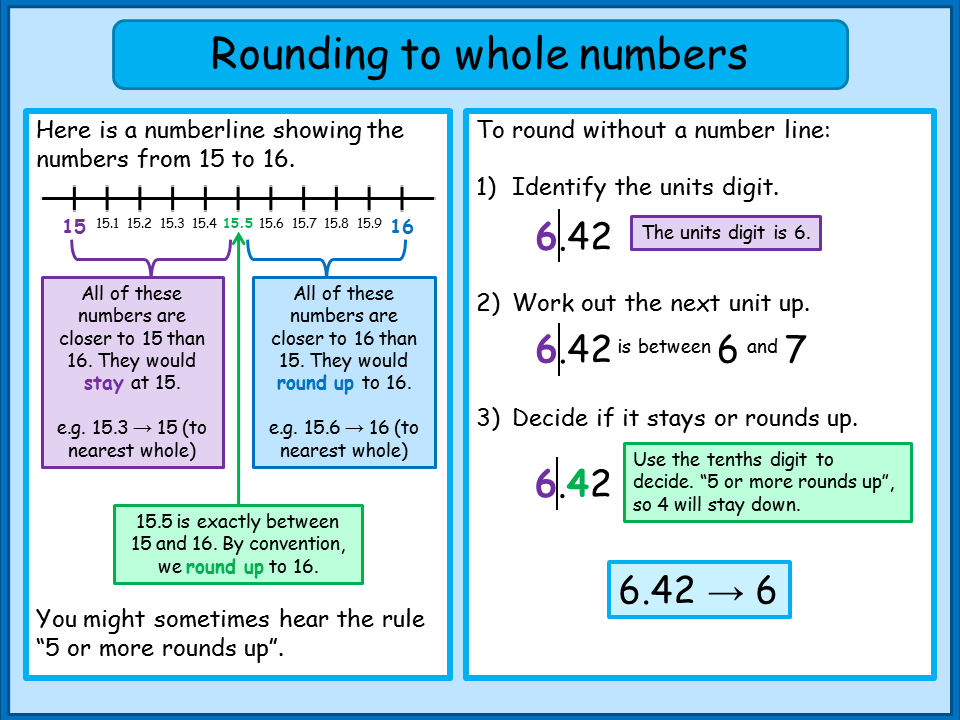
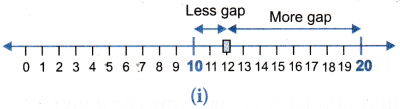How do you Round to the Nearest Ten Thousand 2Similarly, if we take a number say 16, then it is nearer to 20 as compared to 10. So, we will round off 16 to the nearest ten as 20.
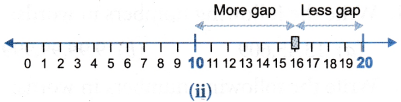How do you Round to the Nearest Ten Thousand 3But if number 15 is considered, which is at equal distance from both 10 and 20, it is also rounded off to 20.
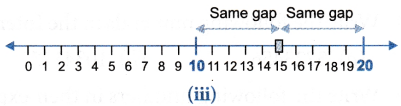How do you Round to the Nearest Ten Thousand 4Similarly,

  1. In 46, the digit in the ones place is 6. Hence, 46 rounded off to the nearest ten is 50.
  2. In 251, the digit in the ones place is 1. Hence, 251 rounded off to the nearest ten is 250.
  3. In 345, the digit in the tens place is 4. Hence, 345 rounded off to the nearest hundred is 300.
  4. In 9157, the digit in the tens place is 5. Hence, 9157 rounded off to the nearest hundred is 9200.
  5. In 5473, the digit at the hundreds place is 4. Hence, 5473 rounded off to the nearest thousand is 5000.

How do you Round to the Nearest Ten Thousand 5
How do you Round to the Nearest Ten Thousand 6

Rounding off a number to the nearest ten thousand

  1. Consider the digit in thousands place of the given number.
  2. If it is less than 5, replace the digits in thousands, hundreds, tens, and ones by 0, keeping the digits in other places as they are.
  3. If it is 5 or more than 5, replace the digits in thousands, hundreds, tens, and ones by 0 and increase the digit in ten thousands by 1.

Examples

  1. In number 18785, the digit in thousands place is 8 and 8 > 5, so when rounded off the number nearest to ten thousand is 20000.
  2. In number 73568, the digit in thousands place is 3 and 3 < 5, so when rounded off the number nearest to ten thousand is 70000.

Rounding off a number to the nearest lakh

  1. Consider the digit in ten thousands place of the given number.
  2. If it is 5 or more than 5, replace the digits in ten thousands, thousands, hundreds, tens, and ones by 0 and increase the digit in lakhs by 1.
  3. If it is less than 5, replace the digits in ten thousands, thousands, hundreds, tens, and ones by 0 keeping the digits in other places as they are.

Examples

  1. In number 560712, the digit in ten thousands place is 6, and 6 > 5, so the rounded off number is 600000.
  2. In number 821058, the digit in ten thousands place is 2, and 2 < 5, so the rounded off number is 800000.

Read More About:

Maths