Vectors
Vectors represent one of the most important mathematical systems, which is used to handle certain types of problems in Geometry, Mechanics and other branches of Applied Mathematics, Physics and Engineering.
Scalar and vector quantities: Those quantities which have only magnitude and which are not related to any fixed direction in space are called scalar quantities, or briefly scalars. Examples: Mass, Volume, Density, Work, Temperature etc. Those quantities which have both magnitude and direction, are called vectors. Displacement, velocity, acceleration, momentum, weight, force are examples of vector quantities.
Representation of vectors
Geometrically a vector is represent by a line segment. For example, \(a=\overrightarrow { AB } \). Here A is called the initial point and B, the terminal point or tip.
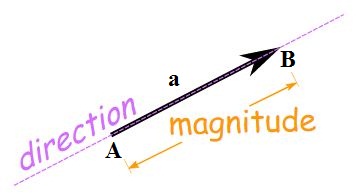 Magnitude or modulus of a is expressed as \(\left| a \right| =\overrightarrow { \left| AB \right| } =\left| AB \right|\)
Magnitude or modulus of a is expressed as \(\left| a \right| =\overrightarrow { \left| AB \right| } =\left| AB \right|\)
Types of vector
- Zero or null vector: A vector whose magnitude is zero is called zero or null vector and it is represented by \(\overrightarrow { O }\).
- Unit vector: A vector whose modulus is unity, is called a unit vector. The unit vector in the direction of a vector is denoted by \(\hat { a }\), read as “a cap”. Thus, \(\left| \hat { a } \right| =1\).
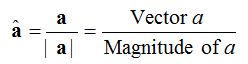
- Like and unlike vectors: Vectors are said to be like when they have the same sense of direction and unlike when they have opposite directions.
- Collinear or parallel vectors: Vectors having the same or parallel supports are called collinear or parallel vectors.
- Co-initial vectors: Vectors having the same initial point are called co-initial vectors.
- Coplanar vectors: A system of vectors is said to be coplanar, if their supports are parallel to the same plane.
Two vectors having the same initial point are always coplanar but such three or more vectors may or may not be coplanar. - Coterminous vectors: Vectors having the same terminal point are called coterminous vectors.
- Negative of a vector: The vector which has the same magnitude as the vector a but opposite direction, is called the negative of a and is denoted by −a. Thus, if \(\overrightarrow { PQ } =a\), then \(\overrightarrow { QP } =-a\).
- Reciprocal of a vector: A vector having the same direction as that of a given vector but magnitude equal to the reciprocal of the given vector a is known as the reciprocal of a and is denoted by a-1. Thus, if |a| = a, \(\left| { a }^{ -1 } \right| =\frac { 1 }{ a }\).
- Localized and free vectors: A vector which is drawn parallel to a given vector through a specified point in space is called a localized vector. For example, a force acting on a rigid body is a localized vector as its effect depends on the line of action of the force. If the value of a vector depends only on its length and direction and is independent of its position in the space, it is called a free vector.
- Position vectors: The vector \(\overrightarrow { OA }\) which represents the position of the point A with respect to a fixed point O (called origin) is called position vector of the point A. If (x, y, z) are co-ordinates of the point A, then \(\overrightarrow { OA } =xi+yj+zk\).
- Equality of vectors: Two vectors and b are said to be equal, if (i) |a| = |b| (ii) They have the same or parallel support and (iii) The same sense.
Properties of vectors
(1) Addition of vectors:

(iii) Addition in component form:
Addition in component form: If the vectors are defined in terms of i, j and k, i.e., if a = a1i+a2j+a3k and b = b1i+b2j+b3k , then their sum is defined as a + b = (a1 + b1)i + a2 (a2 + b2)j + (a3 + b3)k.
Properties of vector addition: Vector addition has the following properties.
- Binary operation: The sum of two vectors is always a vector.
- Commutativity: For any two vectors a and b, a + b = b + a.
- Associativity: For any three vectors a, b and c, a+(b+c)=(a+b)+c.
- Identity: Zero vector is the identity for addition. For any vector
- Additive inverse: For every vector a its negative vector −a exists such that a +(−a) = (−a) + a = O i.e., (−a) is the additive inverse of the vector a.
(2) Subtraction of vectors:
If a and b are two vectors, then their subtraction a − b is defined as a − b = a + (−b) where −b is the negative of b having magnitude equal to that of b and direction opposite to b. If a = a1i+a2j+a3k and b = b1i+b2j+b3k.
Then a – b = (a1 – b1)i + (a2 – b2)j + (a3 – b3)k.
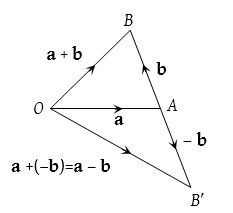
Properties of vector subtraction:
- a – b ≠ b – a
- (a – b) – c ≠ a – (b – c)
- Since any one side of a triangle is less than the sum and greater than the difference of the other two sides, so for any two vectors a and b, we have
(a) |a + b| ≤ |a| + |b
(b) |a + b| ≥ |a| − |b|
(c) |a − b| ≤ |a| + |b|
(d) |a − b| ≥ |a| − |b|
(3) Multiplication of a vector by a scalar:
If a is a vector and m is a scalar (i.e., a real number) then ma is a vector whose magnitude is m times that of a and whose direction is the same as that of a, if m is positive and opposite to that of , if m is negative.
Properties of Multiplication of vectors by a scalar:
The following are properties of multiplication of vectors by scalars, for vectors and scalars m, n.
- m (−a) = (−m) a = −(ma)
- (−m) (−a) = ma
- m (na) = (mn) a = n (ma)
- (m + n) a = ma + na
- m (a + b) = ma +mb
(4) Resultant of two forces

Hence, the angular bisector of two unit vectors a and b is along the vector sum a + b.
Position vector
If a point O is fixed as the origin in space (or plane) and P is any point, then \(\overrightarrow { OP }\) is called the position vector of P with respect to O.
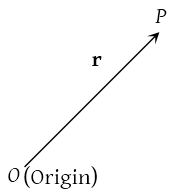 If we say that P is the point r, then we mean that the position vector of P is r with respect to some origin O.
If we say that P is the point r, then we mean that the position vector of P is r with respect to some origin O.

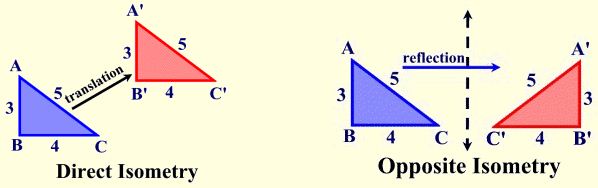
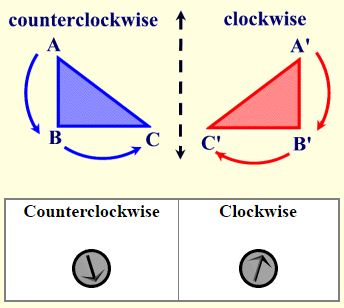
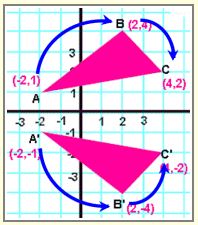 For example, the original image, triangle ABC, has a clockwise orientation – the letters A, B and C are read in a clockwise direction. After the reflection in the x-axis, the image triangle A’B’C’ has a counterclockwise orientation – the letters A’, B’, and C’ are read in a counterclockwise direction.
For example, the original image, triangle ABC, has a clockwise orientation – the letters A, B and C are read in a clockwise direction. After the reflection in the x-axis, the image triangle A’B’C’ has a counterclockwise orientation – the letters A’, B’, and C’ are read in a counterclockwise direction.