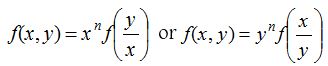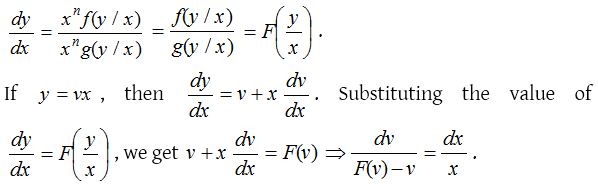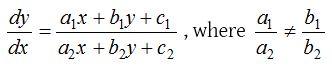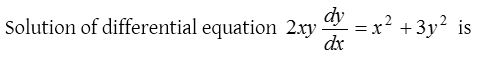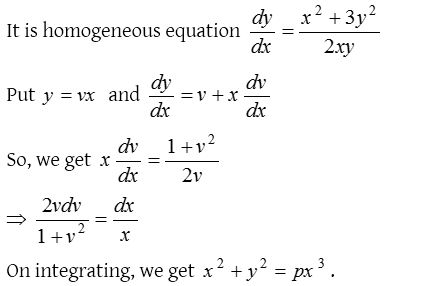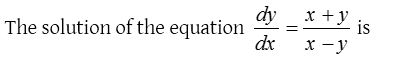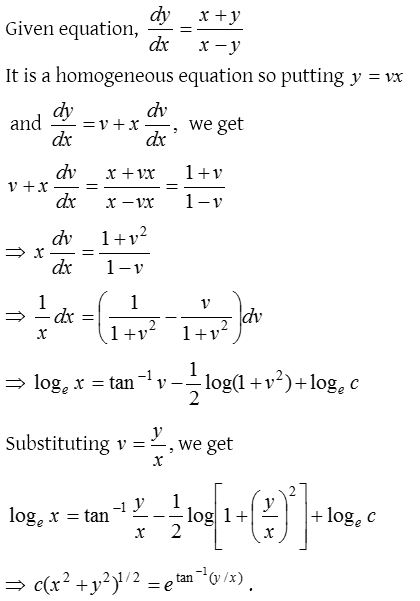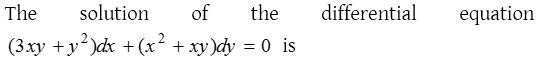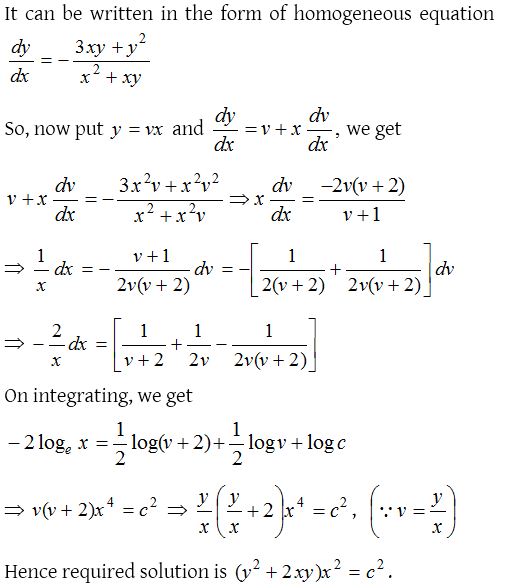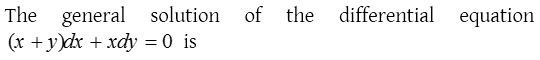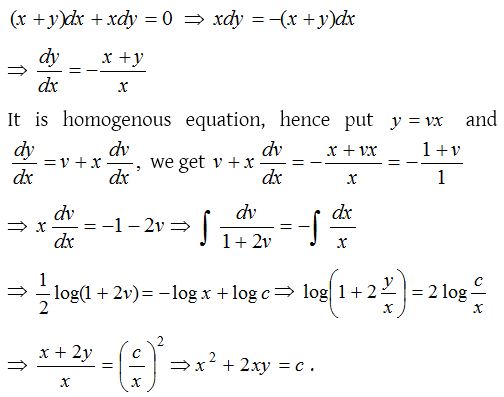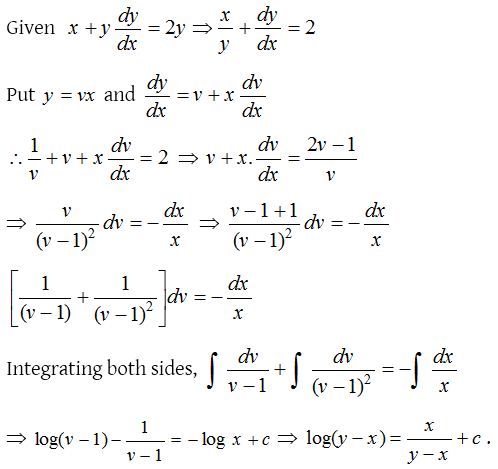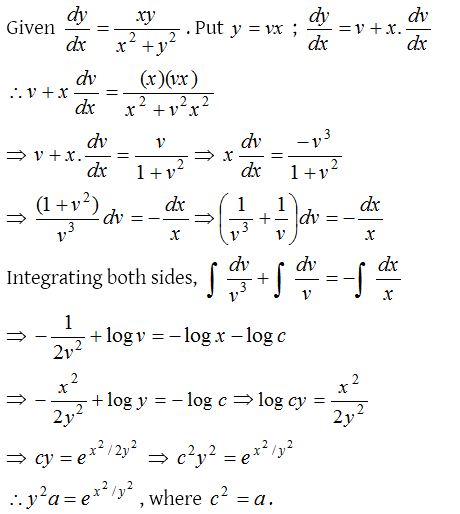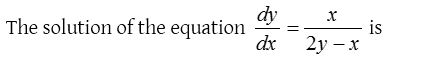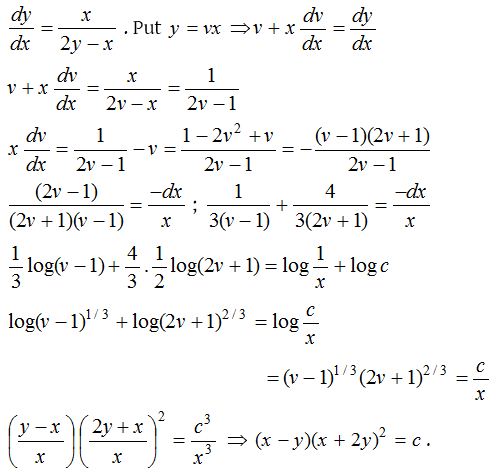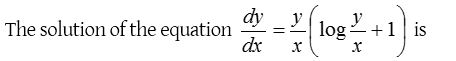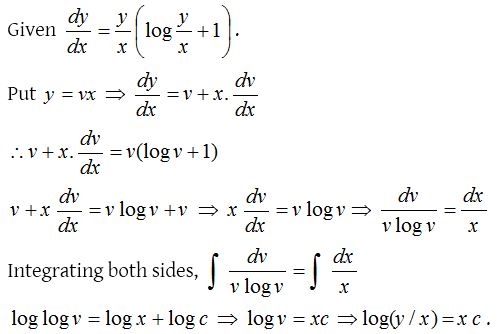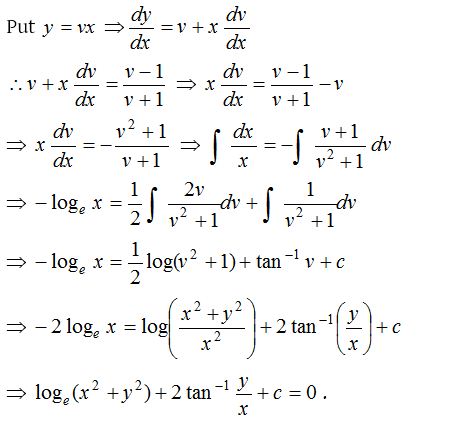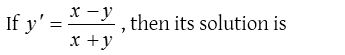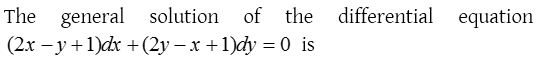Homogeneous differential equation

Differential Equations

by

Differential Equations

An equation involving independent variable x, dependent variable y and the differential coefficients \(\frac { dy }{ dx } ,\frac { { d }^{ 2 }y }{ d{ x }^{ 2 } } ,…..\) is called differential equation.
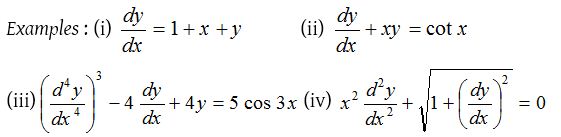
Differential Equations 1

(1) Order of a differential equation:
The order of a differential equation is the order of the highest derivative occurring in the differential equation. For example, the order of above differential equations are 1,1,4 and 2 respectively.
The order of a differential equation is a positive integer. To determine the order of a differential equation, it is not needed to make the equation free from radicals.

(2) Degree of a differential equation:
The degree of a differential equation is the degree of the highest order derivative, when differential coefficients are made free from radicals and fractions. The degree of above differential equations are 1, 1, 3 and 2 respectively.

Formation of differential equation

Formulating a differential equation from a given equation representing a family of curves means finding a differential equation whose solution is the given equation. The equation so obtained is the differential equation of order n for the family of given curves.

Algorithm for formation of differential equations

Step (i): Write the given equation involving independent variable x (say), dependent variable y (say) and the arbitrary constants.
Step (ii): Obtain the number of arbitrary constants in step (i). Let there be n arbitrary constants.
Step (iii): Differentiate the relation in step (i) n times with respect to x.
Step (iv): Eliminate arbitrary constants with the help of n equations involving differential coefficients obtained in step (iii) and an equation in step (i). The equation so obtained is the desired differential equation.

Variable separable type differential equation

(1) Equations in variable separable form:
If the differential equation of the form f1(x) dx = f2(y) dy   …..(i)
where f1 and f2 being functions of x and y only. Then we say that the variables are separable in the differential equation.
Thus, integrating both sides of (i), we get its solution as ∫f1(x) dx = ∫f2(y) dy + c, where c is an arbitrary constant.
There is no need of introducing arbitrary constants to both sides as they can be combined together to give just one.

(2) Equations reducible to variable separable form:
(i) Differential equations of the form \(\frac { dy }{ dx } =f(ax+by+c)\) can be reduced to variable separable form by the substitution ax + by + c = Z.
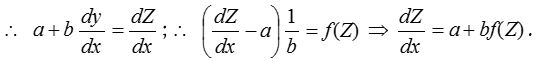
Differential Equations 2
(ii) Differential equation of the form
This is variable separable form and can be solved.
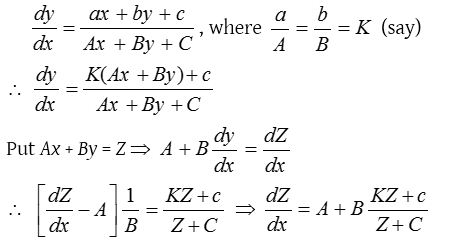
Differential Equations 3

Homogeneous differential equation

Exact differential equation

(1) Exact differential equation:
If M and N are functions of x and y, the equation Mdx + Ndy = 0 is called exact when there exists a function f(x, y) of x and y such that
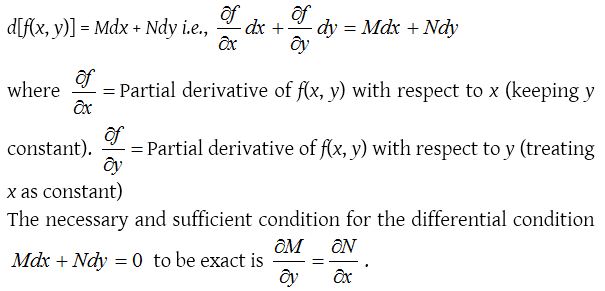
Differential Equations 4
An exact differential equation can always be derived from its general solution directly by differentiation without any subsequent multiplication, elimination etc.

(2) Integrating factor:
If an equation of the form Mdx + Ndy = 0 is not exact, it can always be made exact by multiplying by some function of x and y. Such a multiplier is called an integrating factor.

(3) Working rule for solving an exact differential equation:
Step (i): Compare the given equation with Mdx + Ndy = 0 and find out M and N.
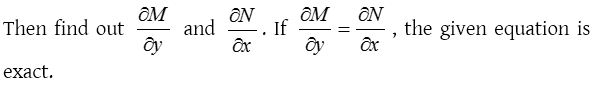
Differential Equations 5
Step (ii): Integrate M with respect to x treating y as a constant.
Step (iii): Integrate N with respect to y treating x as constant and omit those terms which have been already obtained by integrating M.
Step (iv): On adding the terms obtained in steps (ii) and (iii) and equating to an arbitrary constant, we get the required solution.
In other words, solution of an exact differential equation is
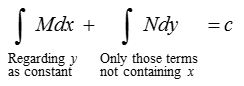
Differential Equations 6

Solution by inspection

If we can write the differential equation in the form f(f1(x))d(f1(x, y)) + ϕ(f2(x))d(f2(x, y)) + ………. = 0, then each term can be easily integrated separately. For this the following results must be memorized.
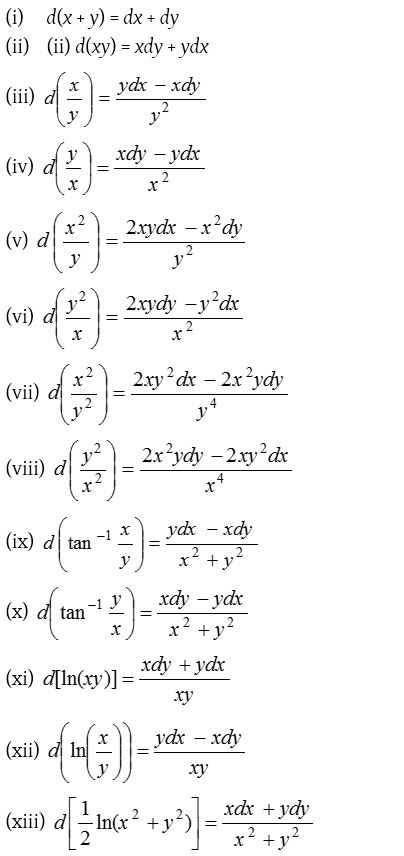
Differential Equations 7
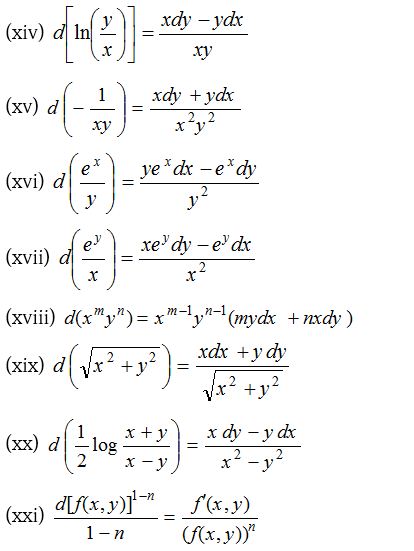
Differential Equations 8

Linear differential equation

Application of differential equation

Differential equation is applied in various practical fields of life. It is used to define various physical laws and quantities. It is widely used in physics, chemistry, engineering etc.
Some important fields of application are:
(i) Rate of change (ii) Geometrical problems etc.

Miscellaneous differential equation

A special type of second order differential equation:
Differential Equations 9

Homogeneous Differential Equations

by

Homogeneous Differential Equations

Homogeneous differential equation

A function f(x,y) is called a homogeneous function of degree if f(λx, λy) = λn f(x, y).
For example, f(x, y) = x2 – y2 + 3xy is a homogeneous function of degree 2.

A homogenous function of degree n can always be written as
Homogeneous Differential Equations 1

If a first-order first-degree differential equation is expressible in the form \(\frac { dy }{ dx } =\frac { f(x,y) }{ g(x,y) }\) where f(x, y) and g(x, y) are homogeneous functions of the same degree, then it is called a homogeneous differential equation. Such type of equations can be reduced to variable separable form by the substitution y = νx. The given differential equation can be written as
Homogeneous Differential Equations 2

On integration, \(\int { \frac { 1 }{ F(v)-v }  } dv\quad =\quad \int { \frac { dx }{ x } +c }\) where c is an arbitrary constant of integration. After integration, v will be replaced by \(\frac { y }{ x }\) in complete solution.

Equation reducible to homogeneous form

A first order, first degree differential equation of the form
Homogeneous Differential Equations 3
This is non-homogeneous.
It can be reduced to homogeneous form by certain substitutions. Put x = X + h, y = Y + k.
Where h and k are constants, which are to be determined.

Homogeneous Differential Equations Problems with Solutions

1.
Homogeneous Differential Equations 4
Solution:
Homogeneous Differential Equations 5
2.
Homogeneous Differential Equations 6
Solution:
Homogeneous Differential Equations 7
3.
Homogeneous Differential Equations 8
Solution:
Homogeneous Differential Equations 9
4.
Homogeneous Differential Equations 10
Solution:
Homogeneous Differential Equations 11
5.
Homogeneous Differential Equations 12
Solution:
Homogeneous Differential Equations 13
6.
Homogeneous Differential Equations 14
Solution:
Homogeneous Differential Equations 15
7.
Homogeneous Differential Equations 16
Solution:
Homogeneous Differential Equations 17
8.
Homogeneous Differential Equations 18
Solution:
Homogeneous Differential Equations 19
9.
Homogeneous Differential Equations 20
Solution:
Homogeneous Differential Equations 21
10.
Homogeneous Differential Equations 22
Solution:
Homogeneous Differential Equations 23
11.
Homogeneous Differential Equations 24
Solution:
Homogeneous Differential Equations 25
12.
Homogeneous Differential Equations 26
Solution:
Homogeneous Differential Equations 27