What is the atomic mass of an element?
Atomic mass
- Atoms are extremely small; the heaviest atoms have masses of about 10–22 g. Even an ultramicrobalance cannot measure the mass of a single atom. However, relative masses of atoms of different elements can be determined. At first, the mass of the lightest atom, hydrogen.
- The SI unit for mass is kilogram (kg).
- The mass of some typical objects which we come across in our daily lives are as shown in Table.
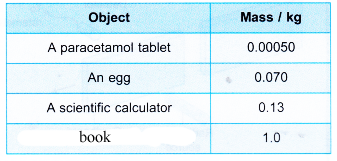
- Atoms and subatomic particles like the proton and neutron have very small masses. If the unit kilogram is used, the mass has to be written in the standard form. A heavy atom like americium-241 has a mass of 4.00 × 10–25 kg. The mass of a proton is 1.67 × 10–27 kg. This means that the kilogram is too large a unit for the mass of atoms.
What is meant by AMU?
- In 1961, International Union of chemists selected the most stable isotope of carbon (C-12 isotope) as standard for comparison the atomic masses of various elements. Atomic mass of an element tells us the number of times an atom of the element is heavier than of the mass of an atom of carbon-12.
- A unit suitable for the mass of atoms and the mass of subatomic particles is the atomic mass unit (u).
- In the definition of the atomic mass unit, the carbon-12 isotope has been chosen to be the reference element. One carbon-12 atom is defined to have a mass of exactly 12 u.
- Atomic mass of an element may be defined as the average relative mass of an atom of the element as compared with mass of an atom of carbon (C-12 isotope) taken as 12 amu.
- Therefore, 1 u is defined as \(\frac { 1 }{ 12 } \) of the mass of a carbon-12 atom.
- It has been found experimentally that the mass of one carbon-12 atom is 1.99265 × 10–26 kg
Therefore, 1 u = \(\frac { 1 }{ 12 } \) × 1.99265 × 10–26 kg
1 u = 1.66 × 10–27 kg - Table gives the mass of some subatomic particles and atoms.
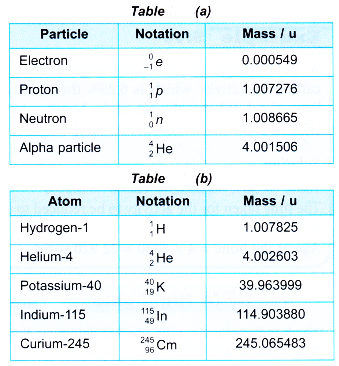
- The values given in Table (b) are the masses of the neutral atoms (which includes the mass of the electrons and not the mass of the nucleus only). For example, the value 4.002 603 u for the mass of a helium-4 atom includes the mass of its 2 electrons.
- When atomic masses are added or subtracted, the answer should be written with the same number of decimal places.
What is the formula for calculating atomic mass?
\(Atomic\quad mass=\frac { Mass\quad of\quad 1\quad atom\quad of\quad the\quad element }{ \frac { 1 }{ 12 } of\quad the\quad Mass\quad of\quad an\quad atom\quad of\quad carbon\quad -\quad 12\quad } \)
Example: The atomic mass of magnesium is 24 u which indicates that one atom of magnesium is 24 times heavier than \(\frac { 1 }{ 12 } \) of a carbon 12 atom.
People also ask
- What is the Definition of Atom and Molecule
- What is Molecular Mass
- What is the Relative Atomic Mass and Relative Molecular Mass of an Element?
- What is One Mole and How many Particles are in a Mole?
- How do you Calculate the Molar Mass of a Substance?
- What is the Molar Volume of a Gas at STP?
- How do you know the Order of Elements in a Chemical Formula
- What is Empirical and Molecular Formula?
- How do you Write a Chemical Equation?
Atomic Mass of Some ElementsGram atomic mass
Gram atomic mass of an element is defined as that much quantity of the element whose mass expressed in grams is numerically equal to its atomic mass. To find gram atomic mass we keep the numerical value the some as the atomic mass, but simply change the units from u to g. for example, atomic mass of aluminium is 27 u. Its gram atomic mass is 27 g.
Gram atomic mass of Isotopes :
Gram atomic mass of Isotopes = \(\frac { { M }_{ 1 }{ X }_{ 1 }+{ M }_{ 2 }{ X }_{ 2 } }{ { X }_{ 1 }+{ X }_{ 2 } } \)
M1 & M2 are relative masses of isotopes and X1 & X2 are relative % content
Example: Chlorine contains two types of atoms having relative masses 35 and 37 and their relative abundance is 3 : 1. In such cases the atomic mass of the element is the average of relative masses of different isotopes of the element.
Atomic mass of chlorine = \(\frac { 35\times 3+37\times 1 }{ 4 } \) = 35.5
| S.no | Element | Symbol | Atomic mass |
| 1 | Hydrogen | H | 1 u |
| 2 | Carbon | C | 12 u |
| 3 | Nitrogen | N | 14 u |
| 4 | Oxygen | O | 16 u |
| 5 | Sodium | Na | 23 u |
| 6 | Magnesium | Mg | 24 u |
| 7 | Aluminium | Al | 27 u |
| 8 | Phosphorus | P | 31 u |
| 9 | Sulphur | S | 32 u |
| 10 | Chlorine | Cl | 35.5 u |
| 11 | Potassium | K | 39 u |
| 12 | Calcium | Ca | 40 u |
| 13 | Iron | Fe | 56 u |
| 14 | Copper | Cu | 63.5 u |
Atomic Mass Problems with Solutions
- What is the difference in mass of a proton and a neutron? Use the data in Table and state your answer in kilograms.
Solution:

- Express the mass of an electron as a fraction of the mass of a proton.
Solution:
