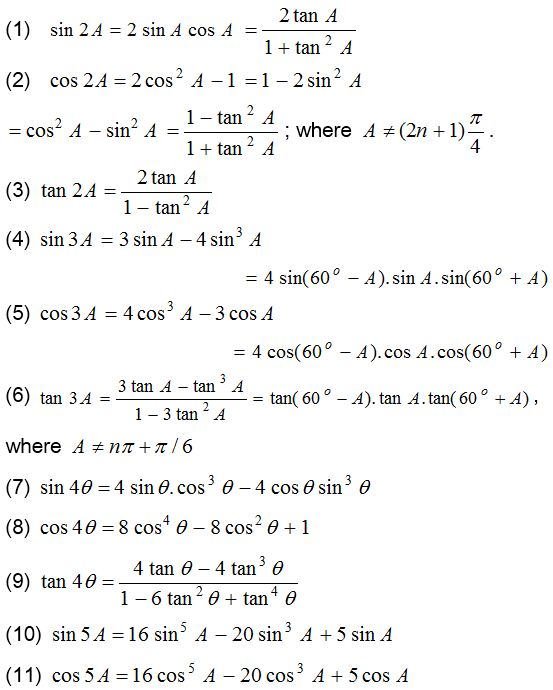Trigonometrical Ratios or Functions
In the right angled triangle OMP, we have base = OM = x, perpendicular =PM = y and hypotenues = OP =r. We define the following trigonometric ratio which are also known as trigonometric function.
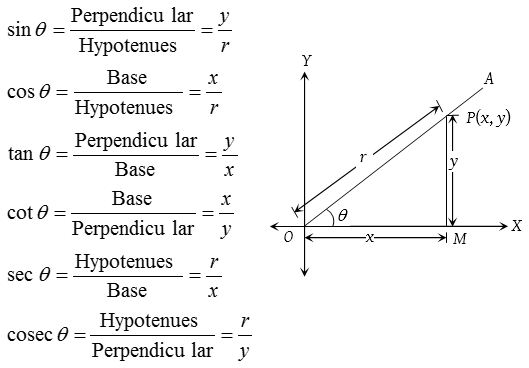
(1) Relation between trigonometric ratios (functions)
- sin θ . cosec θ = 1
- tan θ . cot θ = 1
- cos θ . sec θ = 1
- \(\tan { \theta } =\quad \frac { \sin { \theta } }{ \cos { \theta } } \)
- \(\cot { \theta } =\quad \frac { \cos { \theta } }{ \sin { \theta } } \)
(2) Fundamental trigonometric identities
- sin2 θ + cos2 θ = 1
- 1 + tan2 θ = sec2 θ
- 1 + cot2 θ = cosec2 θ
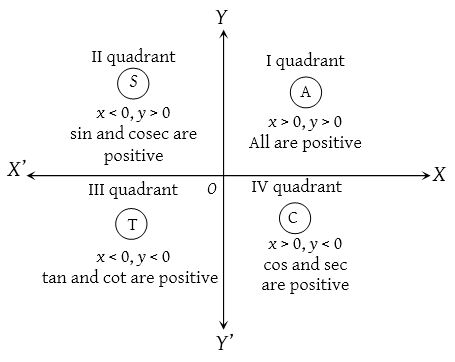
(3) Sign of trigonometrical ratios or functions
Their signs depends on the quadrant in which the terminal side of the angle lies.
In brief: A crude aid to memorise the signs of trigonometrical ratio in different quadrant. “Add Sugar To Coffee”.
 Algorithm: First determine the sign of the trigonometric function.
Algorithm: First determine the sign of the trigonometric function.
If θ is measured from X‘OX i.e., {(π ± θ, 2π – θ)} then retain the original name of the function.
If θ is measured from Y‘OY i.e., {π/2 ± θ, 3π/2 ± θ}, then change sine to cosine, cosine to sine, tangent to cotangent, cot to tan, sec to cosec and cosec to sec.
(4) Variations in values of trigonometric functions in different quadrants:
Let X‘OX and Y‘OY be the coordinate axes. Draw a circle with centre at origin O and radius unity.
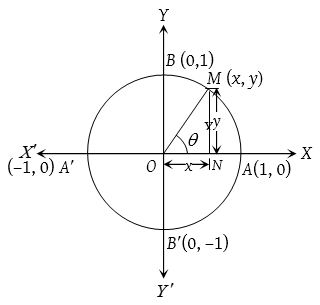 Let M(x, y) be a point on the circle such that then ∠AOM = θ then x = cos θ and y = sin θ; −1 ≤ cos θ ≤ 1 and −1 ≤ cos θ ≤ 1 for all values of θ.
Let M(x, y) be a point on the circle such that then ∠AOM = θ then x = cos θ and y = sin θ; −1 ≤ cos θ ≤ 1 and −1 ≤ cos θ ≤ 1 for all values of θ.
| II-Quadrant (S) | I-Quadrant (A) |
| sin θ ⟶ decreases from 1 to 0 | sin θ ⟶ increases from 0 to 1 |
| cos θ ⟶ decreases from 0 to – 1 | cos θ ⟶ decreases from 1 to 0 |
| tan θ ⟶ increases from – ∞ to 0 | tan θ ⟶ increases from 0 to ∞ |
| cot θ ⟶ decreases from 0 to – ∞ | cot θ ⟶ decreases from ∞ to 0 |
| sec θ ⟶ increases from – ∞ to – 1 | sec θ ⟶ increases from 1 to ∞ |
| cosec θ ⟶ increases from 1 to ∞ | cosec θ ⟶ decreases from ∞ to 1 |
| III-Quadrant (T) | IV-Quadrant (C) |
| sin θ ⟶ decreases from 0 to – 1 | sin θ ⟶ increases from – 1 to 0 |
| cos θ ⟶ increases from – 1 to 0 | cos θ ⟶ increases from 0 to 1 |
| tan θ ⟶ increases from 0 to ∞ | tan θ ⟶ increases from – ∞ to 0 |
| cot θ ⟶ decreases from ∞ to 0 | cot θ ⟶ decreases from 0 to – ∞ |
| sec θ ⟶ decreases from – 1 to – ∞ | sec θ ⟶ decreases from ∞ to 1 |
| cosec θ ⟶ increases from – ∞ to – 1 | cosec θ ⟶ decreases from –1 to –∞ |
Trigonometrical ratios of allied angles
Two angles are said to be allied when their sum or difference is either zero or a multiple of 90°.
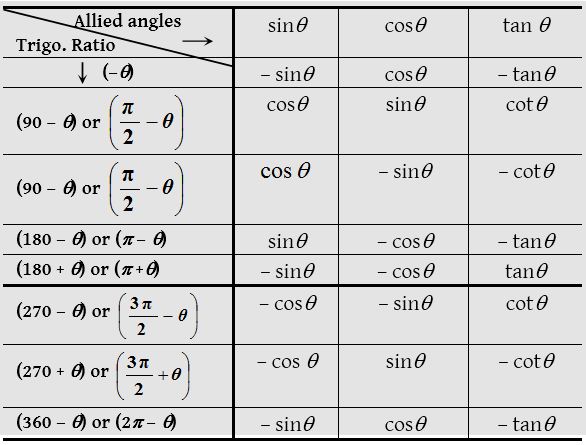
Trigonometrical ratios for various angles
| θ | 0 | ?/6 | ?/4 | ?/3 | ?/2 | ? | 3?/2 | 2? |
| sin θ | 0 | 1/2 | 1/√2 | 3/√2 | 1 | 0 | –1 | 0 |
| cos θ | 1 | √3/2 | 1/√2 | 1/2 | 0 | –1 | 0 | 1 |
| tan θ | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
Trigonometrical ratios for some special angles

Trigonometrical ratios in terms of each other
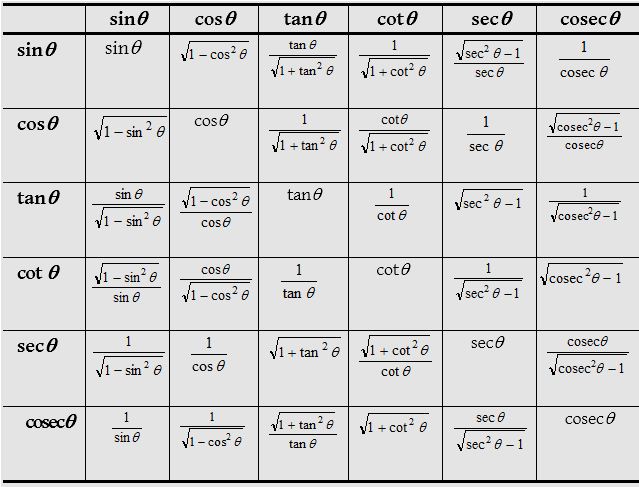
Formulae for the trigonometric ratios of sum and differences of two angles
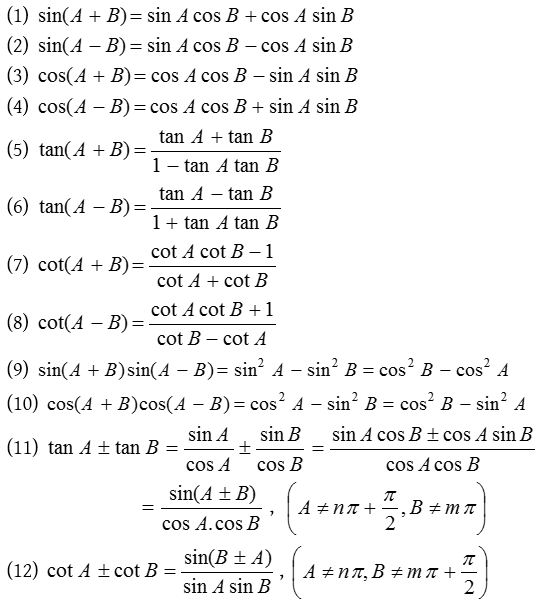
Formulae for the trigonometric ratios of sum and differences of three angles
(1) sin(A + B + C) = sin A cos B cos C + cos A sin B cos C + cos A cos B sin C – sin A sin B sin C
or sin(A + B + C) = cos A cos B cos C(tan A + tan B + tan C – tan A. tan B. tan C)
(2) cos(A + B + C) = cos A cos B cos C – sin A sin B cos C + sin A cos B sin C – cos A sin B sin C
cos(A + B + C) = cos A cos B cos C(1 – tan A tan B – tan B tan C – tan C tan A)

(5) sin(A1 + A2 + …… + An) = cos A1 cos A2 ….. cos An(S1 – S3 + S5 – S7 + ….)
(6) cos(A1 + A2 + …… + An) = cos A1 cos A2 ….. cos An(1 – S2 + S4 – S6 ….)
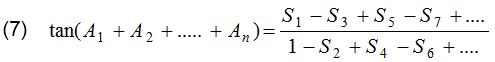
where, S1 = tan A1 + tan A2 + ….. + tan An = The sum of the tangents of the separate angles.
S2 = tan A1 tan A2 + tan A1 tan A3 + …. = The sum of the tangents taken two at a time.
S3 = tan A1 tan A2 tan A3 + tan A2 tan A3 tan A4 + …. = Sum of tangents three at a time, and so on.
If A1 = A2 = …. = An = A, then S1 = n tan A, S2 = nC2 tan2 A, S3 = nC3 tan3 A,……
(8) sin nA = cosn A(nC1 tan A – nC3 tan3 A + nC5 tan5 A – …..)
(9) cos nA = cosn A(1 – nC2 tan2 A + nC4 tan4 A – …..)
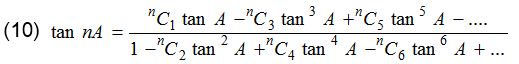
(11) sin nA + cos nA = cosn A(1 + nC1 tan A – nC2 tan2 A – nC3 tan3 A + nC4 tan4 A + nC5 tan5 A – nC6 tan6 A –…..)
(12) sin nA – cos nA = cosn A(–1 + nC1 tan A) + nC2 tan2 A – nC3 tan3 A – nC4 tan4 A + nC5 tan5 A + nC6 tan6 A + …..)
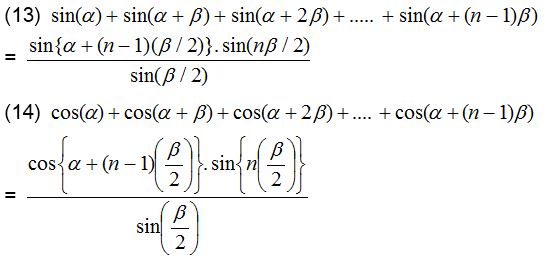
Formulae to transform the product into sum or difference
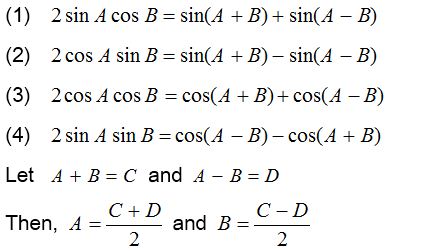
Therefore, we find out the formulae to transform the sum or difference into product.
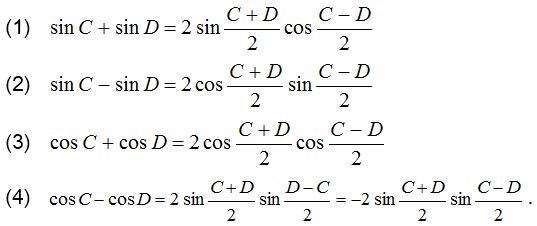
Trigonometric ratio of multiple of an angle