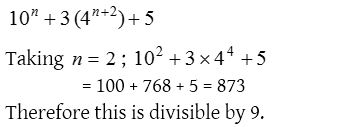What is Mathematical Induction in Discrete Mathematics?
First principle of Mathematical induction
The proof of proposition by mathematical induction consists of the following three steps :
Step I : (Verification step) : Actual verification of the proposition for the starting value “i”.
Step II : (Induction step) : Assuming the proposition to be true for “k”, k ≥ i and proving that it is true for the value (k + 1) which is next higher integer.
Step III : (Generalization step) : To combine the above two steps. Let p(n) be a statement involving the natural number n such that
- p(1) is true i.e. p(n) is true for n = 1.
- p(m + 1) is true, whenever p(m) is true i.e. p(m) is true ⇒ p(m + 1) is true.
Then p(n) is true for all natural numbers n.
Second principle of Mathematical induction
The proof of proposition by mathematical induction consists of following steps :
Step I : (Verification step) : Actual verification of the proposition for the starting value i and (i + 1).
Step II : (Induction step) : Assuming the proposition to be true for k – 1 and k and then proving that it is true for the value k + 1; k ≥ i + 1.
Step III : (Generalization step) : Combining the above two steps. Let p(n) be a statement involving the natural number n such that
- p(1) is true i.e. p(n) is true for n = 1 and
- p(m + 1) is true, whenever p(n) is true for all n, where i ≤ n ≤ m.
Then p(n) is true for all natural numbers.
For a ≠ b, The expression is divisible by
(a) a + b, if n is even.
(b) a – b, if n is odd or even.
Divisibility problems
To show that an expression is divisible by an integer
- If a, p, n, r are positive integers, then first of all we write apn+r = apn . ar = (ap)n . ar.
- If we have to show that the given expression is divisible by c.
Then express, ap = [1 + (ap – 1)], if some power of (ap – 1) has c as a factor. ap = [2 + (ap – 2)], if some power of (ap – 2) has c as a factor.
ap = [k + (ap – k)], if some power of (ap – k) has c as a factor.
Mathematical Induction Problems with Solutions
1. For all positive integral values of n, 32n – 2n + 1 is divisible by
(a) 2
(b) 4
(c) 8
(d) 12
Solution:
Putting n = 2 in 32n – 2n + 1 then, 32(2) – 2×2 + 1 = 81 – 4 + 1 = 78, which is divisible by 2.
2. If n ∈ N, then x2n – 1 + y2n – 1 is divisible by
(a) x +y
(b) x – y
(c) x2 + y2
(d) x2 + xy
Solution:
x2n – 1 + y2n – 1 is always contain equal odd power. So it is always divisible by x + y.
3. If n ∈ N, then 72n + 23n – 3 . 3n – 1 is always divisible by
(a) 25
(b) 35
(c) 45
(d) None of these
Solution:
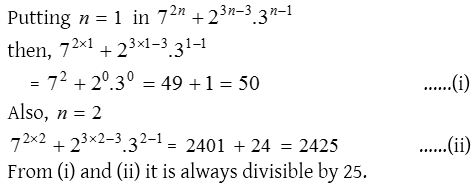
4. If n ∈ N, then 11n + 2 + 122n + 1 is divisible by
(a) 113
(b) 123
(c) 133
(d) None of these
Solution:
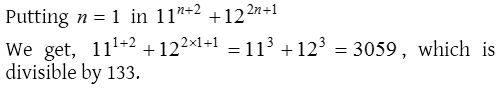
5. The remainder when 599 is divided by 13 is
(a) 6
(b) 8
(c) 9
(d) 10
Solution:
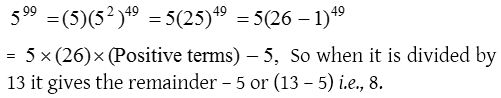
6. When 2301 is divided by 5, the least positive remainder is
(a) 4
(b) 8
(c) 2
(d) 6
Solution:
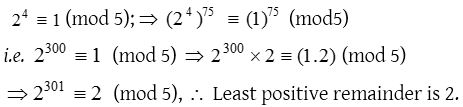
7. For a positive integer n,
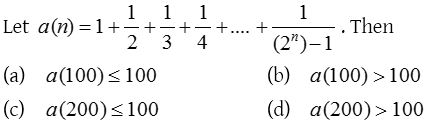
Solution:
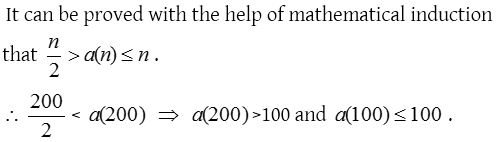
8. 10n + 3(4n + 2) + 5 is divisible by (n ∈ N)
(a) 7
(b) 5
(c) 9
(d) 17
(e) 13
Solution: