Construction Of Similar Triangle As Per Given Scale Factor
Scale factor means the ratio of the sides of the triangle to be constructed with the corresponding sides of the given triangle.
This construction involves two different situations :
(i) The triangle to be constructed is smaller than the given triangle, here scale factor is less than 1.
(ii) The triangle to be constructed is bigger than the given triangle, here scale factor is greater than 1.
Read More:
- Construction Of A Line Segment
- Construction Of The Bisector Of A Given Angle
- Construction Of Perpendicular Bisector Of A Line Segment
- Construction Of An Angle Using Compass And Ruler
Construct A Triangle Similar To A Given Triangle Examples
Example 1: Construct a ∆ABC in which AB = 4 cm, BC = 5 cm and AC = 6 cm. Now, construct a triangle similar to ∆ABC such that each of its sides is two-third of the corresponding sides of ∆ABC. Also, prove your assertion.
Solution. Steps of construction
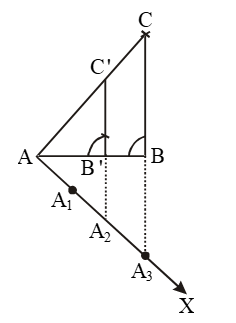 Step I: Draw a line segment AB = 4 cm.
Step I: Draw a line segment AB = 4 cm.
Step II: With A as centre and radius = AC = 6 cm, draw an arc.
Step III: With B as centre and radius = BC = 5 cm, draw another arc, intersecting the arc drawn in step II at C.
Step IV: Join AC and BC to obtain ∆ABC.
Step V: Below AB, make an acute angle ∆BAX.
Step VI: Along AX, mark off three points (greater of 2 and 3 in 2/3) A1, A2, A3 such that AA1 = A1A2 = A2A3.
Step VII: Join A3B.
Step VIII: Since we have to construct a triangle each of whose sides is two-third of the corresponding sides of ∆ABC. So, take two parts out of three equal parts on AX i.e. from point A2, draw
A2B’ || A3B, meeting AB at B’.
Step IX: From B’, draw B’C’ || BC, meeting AC at C’.
AB’C’ is the required triangle, each of the whose sides is two-third of the corresponding sides of ∆ABC.
Justification: Since B’C’ || BC.
So, ∆ABC ~ ∆AB’C’
\( \frac{B’C’}{BC}=\frac{AC’}{AC}=\frac{AB’}{AB}=\frac{2}{3}\text{ }\left[ \frac{AB’}{AB}=\frac{2}{3} \right] \)
Let ABC be the given triangle and we want to construct a triangle similar to ∆ABC such that each of its sides is \(\frac { m }{ n }\) th of the corresponding sides of ∆ABC such that m < n. We follow the following steps to construct the same.
Steps of construction when m > n.
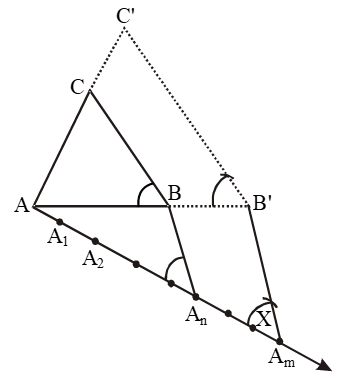
Step I: construct the given triangle by using the given data.
Step II: Take any of the three sides of the given triangle and consider it as the base. Let AB be the base of the given triangle.
Step III: At one end, say A, of base AB construct an acute angle ∠BAX below base AB i.e. on the opposite side of the vertex C.
Step IV : Along AX, mark-off m (large of m and n) points A1, A2,…,Am on AX such that AA1 = A1A2 = ….. = Am-1Am.
Step V : Join An to B and draw a line through Am Parallel to AnB, intersecting the extended line segment AB at B’.
Step VI: Draw a line through B’ parallel to BC intersecting the extended line segment AC at C’.
Step VII: ∆AB’C’ so obtained is the required triangle.
Justification: For justification of the above construction consider triangles ABC and AB’C’. In these two triangles, we have
∠BAC = ∠B’AC’
∠ABC = ∠AB’C’ [∵ B’C’ || BC]
So, by AA similarity criterion, we have
∆ABC ~ ∆AB’C’
\( \Rightarrow \frac{AB}{AB’}=\frac{BC}{B’C’}=\frac{AC}{AC’}\text{ }………\text{ (i)} \)
In D A AmB’, AnB || AmB’.
\( \frac{AB}{BB’}=\frac{A{{A}_{n}}}{{{A}_{n}}{{A}_{m}}} \)
\(\Rightarrow \frac{BB’}{AB}=\frac{{{A}_{n}}{{A}_{m}}}{A{{A}_{n}}}\text{ }\Rightarrow \text{ }\frac{BB’}{AB}=\frac{m-n}{n} \)
\( \Rightarrow \frac{AB’-AB}{AB}=\frac{m-n}{n}\text{ }\Rightarrow \text{ }\frac{AB’}{AB}-1=\frac{m-n}{n} \)
\( \Rightarrow \frac{AB’}{AB}=\frac{m}{n}\text{ }……..\text{ (ii)} \)
From (i) and (ii), we have
\( \frac{AB’}{AB}=\frac{B’C’}{BC}=\frac{AC’}{AC}=\frac{m}{n} \)
Example 2: Draw a triangle ABC with side BC = 7 cm,
∠B = 45º, ∠A = 105º. Then construct a triangle whose sides are (4/3) times the corresponding sides of ∆ABC.
Solution. In order to construct ∆ABC, we follow the following steps:
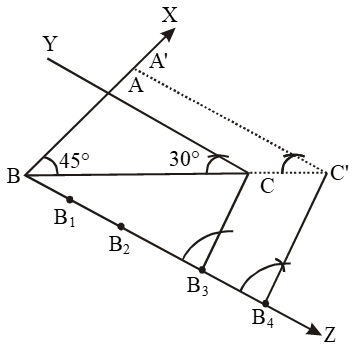
Step I: Draw BC = 7 cm.
Step II: At B construct ∠CBX = 45º and at C
construct ∠BCY = 180º – (45º – 105º) = 30º
Suppose BX and CY intersect at A. ∆ABC so obtained is the given triangle. To construct a triangle similar to ∆ABC,
we follow the following steps.
Step I: Construct an acute angle ∠CBZ at B on opposite side of vertex A of ∆ABC.
Step II: Mark-off four (greater 4 and 3 in 4/3) points
B1, B2, B3, B4 on BZ such that
BB1 = B1B2 = B2B3 = B3B4.
Step III: Join B3 (the third point) to C and draw a line through B4 parallel to B3C, intersecting the extended line segment BC at C’.
Step IV: Draw a line through C’ parallel to CA intersecting the extended line segment BA at A’.
Triangle A’BC’ so obtained is the required triangle such that
\(\frac{A’B}{AB}=\frac{BC’}{BC}=\frac{A’C’}{AC}=\frac{4}{3} \)
Example 3: Construct a triangle similar to a given triangle ABC such that each of its sides is (6/7)th of the corresponding sides of ∆ABC. It is given that
AB = 5 cm, AC = 6 cm and BC = 7 cm.
Solution. Steps of Construction
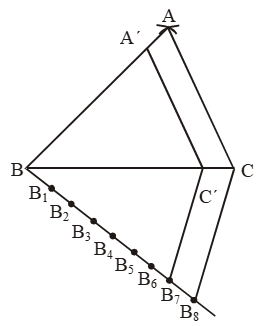
Step I: Draw a line segment BC = 7 cm.
Step II: With B as centre and radius = AB = 5 cm, draw an arc.
Step III : With C as centre and radius = AC = 6 cm, draw another arc, intersecting the arc drawn in step II at A.
Step IV: Join AB and AC to obtain the triangle ABC.
Step V: Below base BC, construct an acute angle ∠CBX.
Step VI: Along BX, mark off seven points B1, B2, B3, B4, B5, B6, B7 such that
BB1 = B1B2 = …… = B6B7.
Step VII: Join B7C.
Step VIII: Since we have to construct a triangle each of whose sides is (6/7)th of the corresponding sides of ∆ABC. So take 6 parts out of 7 equal parts on BX i.e. from B6, Draw B6C´ || B7C, intersecting BC at C´.
Step IX: From C´, draw C´A´ || CA, meeting BA at A´.
∆A´BC´ is the required triangle each of whose sides is (6/7)th of the corresponding sides of ∆ABC.
Example 4: Construct a ∆ABC in which AB = 4 cm, ∠B = 60º and altitude CL = 3 cm. Construct a ∆ADE similar to ∆ABC such that each side of ∆ADE is 3/2 times that of the corresponding side of ∆ABC.
Solution. Steps of construction
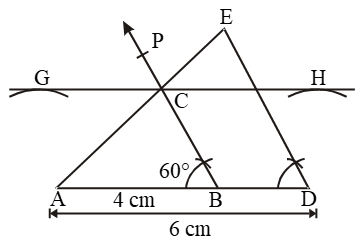
Step I: Draw a line segment AB = 4 cm.
Step II: Construct ∠ABP = 60º.
Step III: Draw a line GH || AB at a distance of 3 cm, intersecting BP at C.
Step IV: Join CA.
Thus, ∆ABC is obtained.
Step V: Extend AB to D such that AD = 3/2 AB = \(\left( \frac{3}{2}\times 4 \right)\) cm = 6 cm.
Step VI: Draw DE || BC, cutting AC produced at E.
Then ∆ADE is the required triangle similar to ∆ABC such that each side of ∆ADE is 3/2 times the corresponding side of ∆ABC.
Proof: Since DE || BC,
we have ∆ADE ~ ∆ABC.
\( \frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}=\frac{3}{2} \)